Graphical Representation
Category : 10th Class
![]() Graphical Representation of Different Forms of Quadratic Equation
Graphical Representation of Different Forms of Quadratic Equation
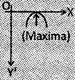
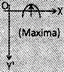
| Characteristic of the function | \[{{b}^{2}}-4\,ac\,<\,0\] | \[{{b}^{2}}-4\,ac\,\,0\] | \[{{b}^{2}}-4\,ac>0\] |
| When 'a' is positive | 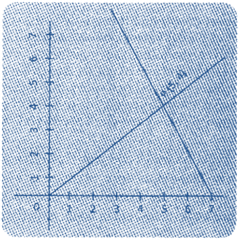 |
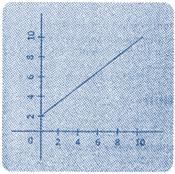 |
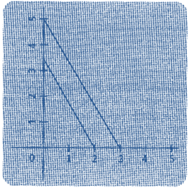 |
| When 'a' negative i.e. a < 0 | 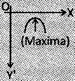 |
 |
 |
![]() Relationship between the Zeroes of the Polynomials and Coefficient of Polynomials
Relationship between the Zeroes of the Polynomials and Coefficient of Polynomials
If \[a{{x}^{2}}+bx+c=0\] is a quadratic equation whose roots are a and p, then the relation between the roots of the equation is given by
Sum of the roots = \[\alpha +\beta -\frac{b}{a},\]
Product of the roots = \[\alpha \beta -\frac{c}{a}.\]
Fora cubic equation \[a{{x}^{3}}+b{{x}^{2}}+cx+d=0\], the relation between the roots whose roots are \[\alpha ,\beta \,and\,\gamma ,\] is given by
Sum of roots = \[\alpha +\beta +\gamma =-\frac{b}{a},\]
Sum of the product of roots = \[\alpha \beta +\beta \gamma +\gamma \alpha =\frac{c}{a}\]
Product of the roots = \[\alpha \beta \gamma =-\frac{d}{a}.\]

![]() The graphical representation of the equation \[f\left( x \right)={{x}^{2}}+2x+10\] is:
The graphical representation of the equation \[f\left( x \right)={{x}^{2}}+2x+10\] is:
(a) Straight line
(b) Circle
(c) Parabola
(d) Ellipse
(e) None of these
Answer: (c)
Explanation
The above given equation is a quadratic equation which traces a parabola on the graph.
![]() The zeroes of the polynomials \[f\left( x \right)=ab{{x}^{2}}+\left( {{b}^{2}}+ac \right)x+bc\,is\_\_\_\_.\]
The zeroes of the polynomials \[f\left( x \right)=ab{{x}^{2}}+\left( {{b}^{2}}+ac \right)x+bc\,is\_\_\_\_.\]
(a) \[\left( \frac{b}{a}\And -\frac{c}{a} \right)\]
(b) \[\left( -\frac{b}{a}\And -\frac{c}{a} \right)\]
(c) \[\left( -\frac{b}{a}\And \frac{c}{a} \right)\]
(d) \[\left( \frac{b}{a}\And \frac{c}{a} \right)\]
(e) None of these
Answer: (b)
Explanation
We have,
\[ab{{x}^{2}}+\left( {{b}^{2}}+ac \right)x+bc\]
\[=ab{{x}^{2}}+{{b}^{2}}x+acx+bc\]
\[=bx\left( ax+b \right)+c\left( ax+b \right)\]
\[=\left( ax+b \right)\left( bx+c \right)\]
Therefore, \[x=\left( -\frac{b}{a}\And -\frac{c}{a} \right)\]
![]() If a and (3 are the roots of the given equation \[2\sqrt{3}{{x}^{2}}+4x-3\sqrt{3}\], then the value of \[\frac{1}{{{\alpha }^{3}}}+\frac{1}{{{\beta }^{3}}}is\_\_\_\_\_.\]
If a and (3 are the roots of the given equation \[2\sqrt{3}{{x}^{2}}+4x-3\sqrt{3}\], then the value of \[\frac{1}{{{\alpha }^{3}}}+\frac{1}{{{\beta }^{3}}}is\_\_\_\_\_.\]
(a) 0
(b) \[-\frac{280\sqrt{3}}{243}\]
(c) \[+\frac{280\sqrt{3}}{243}\]
(d) \[\frac{280}{243}\]
(e) None of these
Answer: (c)
Explanation
The sum of the roots is \[\alpha +\beta =-\frac{b}{a}=-\frac{2}{\sqrt{3}}\]
Product of the roots \[\alpha \beta =\frac{c}{a}=-\frac{3}{2}\]
Now, \[=\frac{1}{{{\alpha }^{3}}}\frac{1}{{{\beta }^{3}}}=\frac{\left( \alpha +{{\beta }^{3}} \right)-3\alpha \beta \left( \alpha +\beta \right)}{{{\left( \alpha \beta \right)}^{3}}}\]
\[=\frac{\frac{-8}{3\sqrt{3}}-\frac{9}{\sqrt{3}}}{-\frac{27}{8}}\]
![]() If \[\alpha \,and\,\beta \] are the roots of the polynomials \[k{{y}^{2}}+6y-18\,such\,that\,{{\alpha }^{2}}+{{\beta }^{2}}=36\] then find the value of k.
If \[\alpha \,and\,\beta \] are the roots of the polynomials \[k{{y}^{2}}+6y-18\,such\,that\,{{\alpha }^{2}}+{{\beta }^{2}}=36\] then find the value of k.
(a) \[\frac{1\pm \sqrt{2}}{2}\]
(b) \[\frac{1\pm \sqrt{3}}{2}\]
(c) \[\frac{1+\sqrt{3}}{2}\]
(d) \[\frac{1\pm \sqrt{5}}{2}\]
(e) None of these
Answer: (d)
Explanation
We have, \[{{\alpha }^{2}}+{{\beta }^{2}}={{\left( \alpha +\beta \right)}^{2}}-2\alpha \beta \]
\[\frac{36}{{{k}^{2}}}+\frac{36}{k}=36\]
\[{{k}^{2}}-k-1=0\]
\[k=\frac{1\pm \sqrt{5}}{2}\]
![]() If a and b are the roots of the equation \[{{m}^{2}}+5m-8\], find a polynomial whose roots are \[2a+1\,and\,2b+1\].
If a and b are the roots of the equation \[{{m}^{2}}+5m-8\], find a polynomial whose roots are \[2a+1\,and\,2b+1\].
(a) \[h(m)=3{{m}^{2}}+4m+1\]
(b) \[k({{m}^{2}}+9m+41)\]
(c) \[({{m}^{2}}+8m-)41\]
(d) \[k({{m}^{2}}-9m-41)\]
(e) None of these
Answer: (a)
Explanation
We have sum of the roots = a + b = - 5
Product of the roots = ab = - 8
Now for the required equation,
Sum of the roots = 2 (a + b) + 2 = - 10 + 2 = - 8
Product of the roots = 4ab + 2(a + b) + 1 = - 41
Therefore, required equation is k \[({{m}^{2}}+8m-)41\].

![]() Based on Cubic Polynomials
Based on Cubic Polynomials
![]() The zeroes of the polynomials\[f(y)={{y}^{3}}-8{{y}^{2}}+24+64\], if two zeroes are equal in magnitude but opposite in sign.
The zeroes of the polynomials\[f(y)={{y}^{3}}-8{{y}^{2}}+24+64\], if two zeroes are equal in magnitude but opposite in sign.
(a) (5, 8, & 9)
(b) \[(2\sqrt{2},-2\sqrt{2}\And 8)\]
(c) \[(-2\sqrt{2},5,\And 8)\]
(d) \[(2\sqrt{2},5\sqrt{2}\And 8)\]
(e) None of these
Answer: (b)
Explanation
If \[\alpha ,\beta \,and\,\gamma \] are the roots of the equation, then sum of the roots \[=\alpha +\beta +\gamma =8\]s
Product of the roots \[=\alpha \beta \,\,\gamma =\,-64\]
Putting the value we have, \[\alpha \beta =-8\]
Therefore, \[\alpha ,2\sqrt{2}=a\,and\,\beta =-2\sqrt{2}\,and\,\gamma =8\]
![]() Find the values of k for which the zeroes of the polynomial \[f(n)={{n}^{3}}+12{{n}^{2}}+39n+k\] are in A.P.
Find the values of k for which the zeroes of the polynomial \[f(n)={{n}^{3}}+12{{n}^{2}}+39n+k\] are in A.P.
(a) 60
(b) 25
(c) - 25
(d) 28
(e) None of these
Answer: (a)
![]() The cubic polynomial whose three roots are 3, -1 and - 3 is:
The cubic polynomial whose three roots are 3, -1 and - 3 is:
(a) \[{{n}^{3}}+{{n}^{2}}-9n-9\]
(b) \[{{n}^{3}}-{{n}^{2}}-9n-9\]
(c) \[{{n}^{3}}+{{n}^{2}}+9n+9\]
(d) \[{{n}^{3}}-{{n}^{2}}+9n+9\]s
(e) None of these
Answer: (a)
![]() If the zeroes of the polynomial\[f(y){{y}^{3}}-3{{y}^{2}}+9y+8\,are\,(p-q),\,p\,and\,(p+q)\]. The value of p and q is:
If the zeroes of the polynomial\[f(y){{y}^{3}}-3{{y}^{2}}+9y+8\,are\,(p-q),\,p\,and\,(p+q)\]. The value of p and q is:
(a) (1, 3)
(b) \[(1,\pm 3)\]
(c) \[(-1,\pm 3)\]
(d) \[(-1,-3)\]
(e) None of these
Answer: (b)
![]() If \[2\pm \sqrt{3}\] are the two zeroes of the polynomial\[f(x)={{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35\], then the other two zeroes of the polynomials f(x) are:
If \[2\pm \sqrt{3}\] are the two zeroes of the polynomial\[f(x)={{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35\], then the other two zeroes of the polynomials f(x) are:
(a) (- 5, 3)
(b) (1, 3)
(c) (- 1, 3)
(d) (- 5, 7)
(e) None of these
Answer: (d)
You need to login to perform this action.
You will be redirected in
3 sec
