10th Class Mathematics Probability

PROBABILITY

FUNDAMENTAL

Probability - A Theoretical Approach

We know, in advance, that the coin can only land in one of two possible ways either head up or tail up (we dismiss the possibility of its ‘landing’ on its edge, which may be possible, for example, if it falls on sand). We can reasonably assume that each outcome, head or tail, is as likely to occur as the other. We refer to this by saying that the outcomes head and tail, are equally likely.

Considering another example of equally likely outcomes, suppose we throw a die once. For us, a die will always mean a fair die. What are the possible outcomes? They are 1, 2, 3, 4, 5, 6. Each number has the same possibility of showing up. So, the equally likely outcomes of throwing a die are 1, 2, 3, 4, 5 and 6.

Are the outcomes of every experiment equally likely? Let us see. Suppose that a bag contains 4 red balls and 1 blue ball, and you draw a ball without looking into the bag. What are the outcomes? Are the outcomes – a red ball and a blue ball equally likely? Since there are 4 red balls and only one blue ball, you would agree that you are more likely to get a red ball than a blue ball. So, the outcomes (a red ball or a blue ball) are not equally likely. However, the outcome of drawing a ball of any colour from the bag is equally likely. So, all experiments do not necessarily have equally likely outcomes.

However, in this chapter, we will assume that all the experiments have equally likely outcomes. In class IX, GMO book, we defined the experiments or empirical probability P (E) of an event E as

\[\text{P(E)=}\frac{\text{Number of trials in which the event happened}}{\text{Total}\,\,\text{number}\,\,\text{of}\,\,\text{trials}}\]

The empirical interpretation of probability can be applied to every event associated with an experiment which can be repeated a large number of times. The requirement of repeating an experiment has some limitations, as it may be very expensive or unfeasible in many situations. Of course, it worked well in coin tossing or die throwing experiments. But how about repeating the experiment of launching a satellite in order to compute the empirical probability of its failure during launching, or the repetition of the phenomenon of an earthquake to compute the empirical probability of a multi storied building getting destroyed in an earthquake.

In experiments where we are prepared to make certain assumptions, the repetition of an experiment can be avoided, as the assumptions help in directly calculating the exact (theoretical) probability, The assumption of equally likely outcomes (which is valid in many experiments, as in the two examples above, of a coin and of a die) is one such assumption that leads us to the following definition of probability of an event.

The theoretical probability of an event E, (also called classical probability) is defined as

\[\text{P(E)=}\frac{\text{Number of outcomes favourable to E}}{\text{Number}\,\,\text{of}\,\,\text{all}\,\,\text{possible}\,\,\text{outcomes}\,\,\text{of}\,\,\text{the}\,\,\text{experiment}}\]

Where we assume that the outcomes of the experiment are equally likely. This definition was given by mathematician Laplace in 1795.

Let us find the probability for some of the events associated with experiments where the equally likely assumption holds.

Example: Find the probability of getting a head when a coin is tossed once. Also find the probability of getting a tail.

Solution: In the experiment of tossing a coin once, the number of possible outcomes is two – Head (H) and Tail (T). Let E be the event ‘getting a head’. The number of outcomes favourable to E, (i.e. of getting’s ahead) is 1. Therefore,

\[\text{P(E)=P(head)=}\frac{\text{Number of outcomes favourable to E}}{\text{Number}\,\,\text{of}\,\,\text{all}\,\,\text{possible}\,\,\text{possible}\,\,\text{outcomes}}\text{=}\frac{\text{1}}{\text{2}}\text{;P(tail)=1-P(head)=1-}\frac{\text{1}}{\text{2}}\text{=}\frac{\text{1}}{\text{2}}\]

Example: A bag contains a red ball, a blue ball and a yellow ball, all the balls beings of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the (i) yellow ball? (ii) red ball? (iii) blue ball?

Ans. The number of possible outcomes = 3 and number of outcomes favourable to event (getting yellow ball) =1   

\[\Rightarrow \]   \[P(Yellow)=\frac{1}{3}\]

No. of outcomes favourable to event (getting red ball) = 1

\[\Rightarrow \]   \[P(red)=\frac{1}{3}\]

Similarly, \[P(blue)=\frac{1}{3}\]

Here, we also note that P(yellow) + P(red) + P(blue)

            \[=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1\]

That is, sum of probabilities of all elementary events of an experiment is 1.

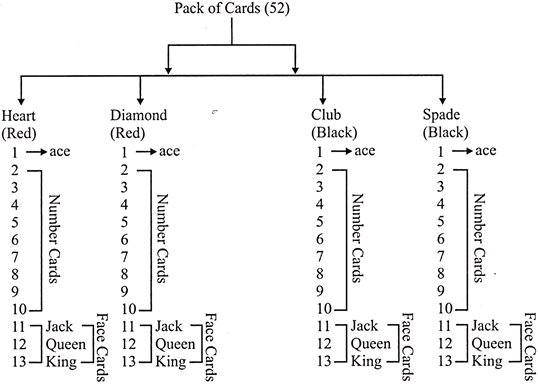
Understanding probability questions based on pack of cards