12th Class Mathematics Relations and Functions Notes - Mathematics Olympiads -Maxima Minima Function

                                                                                            Maxima and Minima of the Function

• Local maximum: A function \[y=f(x)\]is said to have local maximum value at a point\[x=a.\]

If \[f(x)\le f(a)\]\[\forall x\in (a-h,a+h)\]and \[h>0\]

i.e.\[f(a)\] is the greatest value of all values of \[f(x)\]in the interval\[(a-h,a+h)\]

The point\[x=a\]is said to be the point of local maximum of the function

·                    

• Local minimum: A function\[y=f(x)\]is said to have a local minimum value at a point \[x=a.\] If

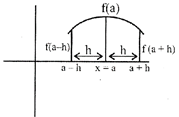
\[f(x)\ge f(a)\]\[\forall x\in (a-h,a+h)\]for \[h>0\] i.e.\[f(a)\] is the smallest value of all the value of \[f(x)\] in the

interval \[(a-h,a+h)\]

The Point\[x=a\] is said to be the point of local minimum of the function\[f(x)\].

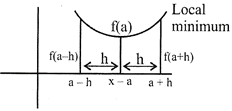
Note: The points at which the function attains either its maximum value or minimum value are said to be the extreme points of the function. Both the local maximum value and local minimum value of the function is said to be extreme value of the function.

It is also said to be the relative maximum value and relative minimum value of the function respectively.

• Working rule to determine the point of local maxima and minima.

1. By 1st derivative method:

Procedure:

(i) First of all find\[f'(x)\]and put\[f'(x)=0\]

(ii) Solve it\[f'(x)=0\]and find the value of x.

(iii) Let \[x=\alpha \]or\[\beta \]or\[\gamma \]etc.

These points are said to be stationary points or critical points.

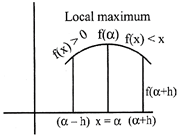
Let\[x=\alpha \]at any point

(a) If \[f'(x)\] changes sign from positive to negative as x increase through a then\[x=\alpha \]is point of maximum.

(b) If \[f'(x)\] changes sign from negative to positive as x increase through\[\alpha \]. Then\[x=\alpha \]is said to be the point of the minimum.

(c) If \[f'(x)\] does not change the sign as x increases through \[\alpha ,\] then\[x=\alpha \] is neither the point of maximum nor the point of minimum. Hence it is said to be the point of inflexion.

·               

• By Second Derivative Test:

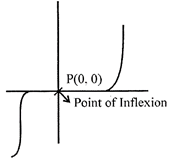
(i)  First of all find\[f'(x)\] & \[f''(x)\]of the given function\[y=f(x).\]

(ii) Then put \[f'(x)=0\] to find the value of x. Let\[x=\alpha ,\beta \]and\[\gamma \]

(a) If \[f''(x)<0,\]at\[x=\alpha ,\] then \[\alpha \] is said to be the point of local maximum and\[f(\alpha )\]is the maximum value of the function \[y=f(x).\]

(b) If \[f''(x)>0\]at \[x=\alpha ,\] then \[\alpha \] is said to be the point of local minimum and\[f(\alpha )\]is the minimum value of the function \[y=f(x).\]

(c) If\[f''(\alpha )=0\]then we cannot state anything about the function and we proceed the further derivatives and applying the same rule to check the maximum and minimum point of the function.

3. Greatest and least value of the function in the closed interval or (Absolute Maximum & Absolute Minimum).

(i) If a function\[y=f(x)\]is differentiable & continuous in the closed interval\[[a,b],\]then it has the greatest or least value i.e. the greatest/absolute maximum value of\[f(x)=\]maximum \[\{f(a),\]\[f(b),\]\[f(a)\]….value of\[f(x)\]at all critical points in\[(a,b)\}.\] The least/absolute minimum value of\[f(x)=\]Minimum \[\{f(a),\]\[f(b),\]...value of\[f(x)\]at all critical points in\[(a,b)\}.\]

• Rolle’s Theorem:

If function\[y=f(x)\]defined on the closed interval\[[a,b],\]is

(a) continuous on \[[a,b]\]

(b) differentiable on \[(a,b)\]

(c) \[f(a)=f(b)\]

Then there exists at least one real number,\[c\in (a,b)\]such that \[f'(c)=0\]i.e. the tangent of the curve at\[x=c\]is parallel to x-axis.

• Lagrange's Mean Value Theorem:

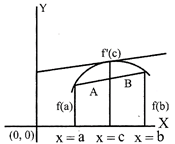
If function\[y=f(x)\]is defined in the closed interval \[[a,b],\] is

(a) continuous on \[[a,b]\]

(b) differentiable on \[[a,b]\] then there exists atleast one real number,\[c\in (a,b)\]such that

\[f'(c)=\frac{f(b)-f(a)}{b-a}\]

Hence, we can say that the tangent to the curve at\[x=c\]is parallel to the chord of line joining A and B.

At\[x=a\]&\[x=b.\]