Notes - Mathematics Olympiads -Relations Functions
Category : 12th Class
Relations and Functions
Now, \[~A\times B=\{1,\,2,\,3,\,4,\}\times \{2,3\}=\{(1,\,2),\,(2,\,2),\,(3,\,2),\,(4,\,2),\,(1,\,3),\,(2,\,3),\,(3,\,3),\,(4,\,3)\}\]
Let we choose an arbitrary set:
R = [(1, 2), (2, 2), (1, 3), (4, 3)]
Then R is said to be the relation between a set A to B.
\[R=\{(x,\,y):x\in A\,\,\,and\,\,\,y\in B\}\]
Note: the 2nd element in the ordered pair (x, y) is the image of 1st element Sometime, it is said that a relation on the set A means the all members / elements of the relation R be the elements / members of\[A\times A\].
Solved Example
Sol. \[\because A=\{1,\,2,\,3\}\]
\[A\times A=\{(1,\,1),\,(2,\,2),\,(3,\,3),\,(2,\,1),\,(3,\,1),\,(1,\,2)\,(3,\,2),\,(1,\,3),\,(2,\,3)\}\]
\[\because \,\,\,\,\,\,\,x<y\]
\[\therefore \,\,\,\,\,\,\,R=\{(x,\,y):x<y,\,\,and\,\,x,\,y\in A\}=\{(1,\,2),\,(2,\,3),\,(1,\,3)\}.\]
Note: Let a set A has m elements and set B has n elements. Then \[n(A\times B)\] be \[m\times n\] elements so, total no. of relation from A to B or between A and B be\[{{2}^{m\,\,\times \,\,n}}\].
(i) Void Relation: A relation R on a set be said to be void or empty relation, if no element of A is related to any elements A.
e.g A relation on set A = {1, 2, 3, 4} defined as
\[R=\{(x,y):x+y=8\}.\]
It is void relation on A because, sum of any two element of \[A\times A\] can not be 8.
(ii) Universal relation: A relation on a set A is said to be universal relation. If each element of A is related to or associated with every element of A.
(iii) Identity Relation:- A relation \[{{l}_{x}}\{(x,\,x):x\in A\}\] an a set A is said to be identity relation on A.
(iv) Reflexive relation: A relation R on the set A is said to be the reflexive relation. If each and every element of set A is associated to itself. Hence, R is reflexive iff
\[(a,\,a)\in R\,\,\forall \,\,a\in A.\]
i.e. \[aRa\,\,\,\forall \,\,a\in A\]
(v) Symmetric relation: A relation R on a set A is said to be symmetric relation iff
\[(x,\,\,y)\in R\Rightarrow (y,\,x)\in R\,\,\forall \,\,x,\,\,y\in A.\]
i.e.\[x\,R\,y\Rightarrow y\,R\,x\,\,\forall \,\,x,\,\,y\in R\]
\[\because \,\,xRy\] is read as \[x\] is R-related to \[y\].
(vi) Antisymmetric relation: A relation which is not symmetric is said to be antisymmetric relation.
(vii) Transitive relation: Let A be any non-empty set. A relation R on set A is said to be transitive
relation R iff \[(x,\,y)\in R\] and \[(y,\,z)\in R\]
then \[(x,\,z)\in R\,\,\forall \,\,x,y,z\in R.\]
i.e. \[xRy\] and \[yRz\Rightarrow xRz\,\,\forall \,\,x,y,z\in R.\]
(viii) Equivalence Relation: A relation R on a set A is said to be an equivalence relation on A iff
(i) It is reflexive i.e. \[(x,y)\in R\,\,\forall \,\,x\in R\]
(ii) It is symmetric i.e. \[(x,y)\in R\,\,\Rightarrow (x,\,y)\,\,\in \,\,\,R\,\,\forall \,\,x,\,y\in R.\]
(iii) It is transitive i.e., \[(x,y)\in R\]and\[(y,\,z)\in R\], then \[(x,\,z)\in R\]\[\forall \,x,\,\,y,\text{ }z\text{ }\in \text{ }R\]
Solved Example
\[A\times A=\{(1,1),(2,1),(3,1),(4,1),(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(4,3),(1,4),(2,4),(3,4),(4,4)\}\]
\[{{R}_{1}}=\{(1,1),(2,2),(3,2),(2,3),(3,3)(4,4)\}\]
\[{{R}_{2}}=\{(2,2),(1,3),(3,3),(3,1)(1,1)\}\]
\[{{R}_{3}}=\{(1,1),(2,2),(3,4),(3,3),(4,4)\}\]
State about \[{{R}_{1}},\,\,{{R}_{2}}\]and \[{{R}_{3}}\] Are they reflexive, symmetric, antisymmetric or transitive relations?
Sol. \[{{R}_{1}}\] is symmetric as well as transitive relation for \[{{R}_{2}}.\,\,{{R}_{2}}\]is not reflexive because \[(4,4)\notin {{R}_{2}}.\] But \[{{R}_{2}}\] is symmetric as well as transitive.
Now, \[{{R}_{3}}\]is reflexive as well as antisymmetric because \[(3,4)\notin {{R}_{3}}\] but \[(4,3)\notin {{R}_{3}}.\]
Concept of function play a very vital role in mathematics (either pure mathematics or applied mathematics). In the secondary school classes, we will learn about real value function only.
(a) Function as an operator.
(b) Function as a relation.
(c) Function as a mapping.
Function is an operator in which we study the relation between independent and dependent real variable/input or output variable.
|
Input |
f |
Output |
e.g. y=f(x)
Let A and B be two non-empty sets. Each element in the set A associated with unique element in set B is said to be function or mapping from A to B.
i.e. f : A \[\to \] B. e. g. y = f(x)
x is said to be independent variable and y is said to be dependent variable.
All elements of set A is said to be domain of f and all elements of set B is said to be co-domain of f as well as all images of each element of set A in B said to be the range of the function f.
\[y=f(x)\Rightarrow f(A)\subseteq B.\]e.g.\[y=f(A)\le B.\]
Relation: Relation on a set is the Cartesian product of two non-empty sets.
Function is a relation but relation may be or may not be function because function has some silent features. Some silent features of a function f.
e.g. f : A\[\to \]B
(i) For every \[x\in A\], \[y\in B\] s. t \[y=f(x).\] i.e. each element of set A has image in B. But there may be an element in B which is not the image of element of A.
(ii) Same element of A can not be associated to distinct element of B. i.e. the image of each element of set A has unique. But the distinct element of A may be associated to same element of B.
Functions are of two types: Into function and onto function (surjective function)
(i) Into function are of two types:
(a) One-one into function (Injective function)
(b) Many-one into function
(ii) Onto function are of two types:
(a) One-one onto function (bijective function)
(b) Many-one onto function
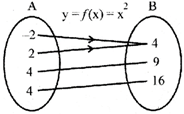
\[y=f(x)={{x}^{3}}\] is an odd function.
(i) A given function can be expressed as the sum of an even and odd function. It can be written as
\[f(x)=\left\{ \frac{1}{2}[f(x)+f(-x)]+\frac{1}{2}[f(x)-f(-x)] \right\}\]
where\[f(x)+f(-x)\] is said to be even function and\[f(x)-f(-x)\] is the odd function.
(ii) \[f(x)=0\]is the only function which is both even and odd function.
(iii) Graph of the even function is symmetric about they-axis.
(iv) Graph of the odd function is symmetric about the origin i.e
(a) lf\[f(x)\] is an even function then\[f'(x)\] is an odd function provided\[f(x)\] is differentiable on R.
(b) lf\[f(x)\] is an odd function then\[f'(x)\] is an even function provided\[f(x)\] is differentiable on R.
(i) \[y=f(x)={{x}^{2}}+\log x\]
(ii) \[y=f(x)={{x}^{3}}+{{\sin }^{2}}x\]
(i) \[xy=\sin (x+y)\]
(ii) \[\log {{x}^{y}}=2{{x}^{2}}\sin y.\operatorname{cotC}.\]
where C = constant,
Domain of f = R
Range of f = | C |
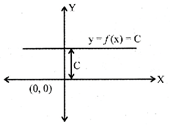
Note: The graph of the constant function is a straight line which is parallel to x - axis.
The domain of f = R
Range at f = R
Here R= Real Number
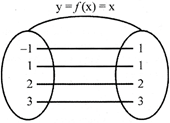
Note: The graph of the identity function is a straight line which is passed through the origin & it is equally inclined to the both the axes.
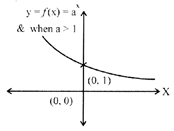
A function f: R\[\to \]R is defined as
\[y=f(x)={{a}^{x}}\], where \[a>0\]& \[a\ne 1\]
is said to be exponential function
The Domain of f = R
Range of \[f=(0,\infty )\to {{R}^{+}}\]
Note: The graph of the exponential function is sketched below.

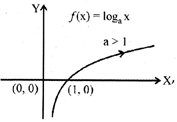
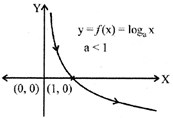
Logarithmic function: A function f: \[(0,\infty )\to R\] defined as \[y=f(x)=lo{{g}_{a}}x,\]\[a\ne 1\,\,\forall \,\,x\in {{R}^{+}}\] is called a logarithmic function.
The domain of\[f=(0,\infty )={{R}^{+}}\]
and range of\[f=(-\infty ,\infty )=R\].
The graph of the function is as shown below.
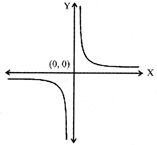
Note: Sometime, \[{{\log }_{e}}x\] is denoted as in\[x\].
The domain of\[f=R-[0]\]
and range of\[f=R-[0]\].
The graph of this function is as shown below:
A function \[f=R\to R\] defined as
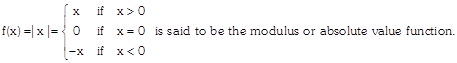
The domain of\[f=(-\infty ,\infty )=R\]
Range of\[f=(0,\infty )\].
The graph of this function is as shown below:
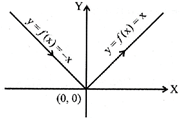
The function\[f:R\to R\] defined as\[f(x)=[x]\] is said to be the greatest integer (step or integral) function.
[x] = integral part of x or greatest integer less than x
Domain of\[f=(-\infty ,\infty )=R\]
Range of f = z = integer number.
The graph of this function is as shown below.
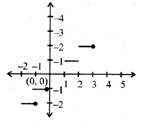
Domain of\[f=(-\infty ,\infty )=R\]
Range of\[f=[0,1)\].
The graph of this function is as shown below.
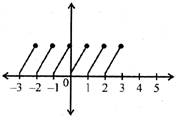
\[\Rightarrow \{[x]\}=0\]
\[\Rightarrow 0<\{x\}<1\]
![]()
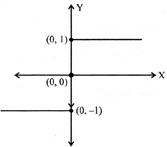
The function\[f:R\to R\] defined as

Domain of\[f=(-\infty ,\infty )=R\]
Range of\[f=\{-1,\,\,0,\,\,1\}\].
The graph of signum function can be sketched as shown below:
|
Function |
Domain |
Range |
|
\[y=\sin x\] |
R |
\[[-1,\,\,1]\] |
|
\[y=\cos x\] |
R |
\[[-1,\,\,1]\] |
|
\[y=\tan x\] |
\[R-\left( \frac{\pi }{2} \right)\] |
R |
|
\[y=\cot x\] |
\[R-(\pi )\] |
R |
|
\[y=\sec x\] |
\[R-\left( \frac{\pi }{2} \right)\] |
\[R-(0,\,\,1)\]or\[(-\infty ,-1]\cup [1,\infty )\] |
|
\[y=co\sec x\] |
\[R-(\pi )\] |
\[(-\infty ,-1]\cup [1,\infty )\] |
|
Function |
Domain |
Range |
|
\[y={{\sin }^{-1}}x\] |
\[-1\le x\le 1\] |
\[\left[ \frac{-\pi }{2},\frac{\pi }{2} \right]\] |
|
\[y={{\cos }^{-1}}x\] |
\[-1\le x\le 1\] |
\[[0,\,\,\pi ]\] |
|
\[y={{\tan }^{-1}}x\] |
\[-\infty <x<\infty \] |
\[\left[ \frac{-\pi }{2},\frac{\pi }{2} \right]\] |
|
\[y={{\cot }^{-1}}x\] |
\[-\infty <x<\infty \] |
\[(0,\,\,\pi )\] |
|
\[y={{\sec }^{-1}}x\] |
\[R-(-1,\,\,1)\] |
\[[0,\,\,\pi ]-\frac{\pi }{2}\] |
|
\[y=co{{\sec }^{-1}}x\] |
\[R-(-1,\,\,1)\] |
\[\left[ \frac{-\pi }{2},\frac{\pi }{2} \right]-\left\{ \left. 0 \right) \right.\]. |
Let f: A\[\to \]B and: B\[\to \]C be defined as
f = {(p, a), (q, c), (r, b), (s, a)}
f = {(a, /), (b, /), (c, m), (q, m)}
Then
\[(gof)(p)=g\,(f\,(p))=g\,(a)=/\]
\[(gof)(q)=g\,(f\,(q))=g\,(c)=m\]
\[(gof)(r)=g\,(f\,(r))=g\,(b)=/\]
\[(gof)(s)=g\,(f\,(s))=f\,(a)=/\]
Thus (gof): A\[\to \]C be written as
gof = {(p, /), (r, /), (s, /), (q, m)}.
Let f : A\[\to \]B & g : B\[\to \]C be two function
\[=f(x)\,\,\forall \,\,x\in \,\,\,R\] ........ (1)
If T is the smallest positive real number, and satisfies the condition\[(1)\], then T is said to be period or fundamental period of f(x).
(i) First of all put f (x + T) = f (x) to solve the above equation & find the positive value of T.
(ii) If the value of T, independent of x is obtained, then f (x) will be the periodic function with period T otherwise it is non-periodic function.
(i) \[\sin x,\] \[\cos x,\]\[\cos ecx,\]\[\sec x\]are periodic functions with period \[2\pi .\]
(ii) \[\tan x,\]\[\cot x\]are also the periodic functions with period \[\pi .\]
(iii) \[|\sin x|,\]\[|\cos x|,\]\[|tanx|,\]\[|\operatorname{cosec}x|,\]\[|\cot x|and|sec\,x|\]are the periodic functions with period \[\pi .\]
(iv) \[{{\sin }^{n}}x,\]\[co{{s}^{n}}x,\]\[\cos e{{c}^{n}}x\And {{\sec }^{n}}x\]are the periodic functions with period \[\pi \] when n is even. Otherwise they are periodic function with period \[2\pi \]when n is odd.
(v) If f(x) is the periodic function with period T, then K f (ax + b) is also a periodic function with period \[\frac{T}{|a|}\] where a, b & \[K\in R\] and a & \[K\ne 0.\]
(vi) If f (x) is the periodic function with period T then \[\sqrt{f(x)}\] and \[\frac{1}{f(x)}\] will be the periodic function with same period T.
(vii) Constant function is a periodic function with no fundamental period.
Solved Examples
Sol. To define the f (x), we have f (x)>0.
\[\Rightarrow {{x}^{2}}-3x+2>0\]
\[\Rightarrow {{x}^{2}}-2x-x+2>0\]
\[\Rightarrow (x-2)(x-1)>0\]
\[\Rightarrow x<1\,\,or\,\,x>2\]
So, domain of f = \[(-\infty ,1)\cup (2,\infty ).\]
Sol. Obviously.
Domain of f \[=(-\infty ,\infty )=R\]
Now for range
\[\because y=\frac{x}{1+{{x}^{2}}}\]
\[\Rightarrow y.\,\,{{x}^{2}}-x+y=0\]
For x to be real
\[D\ge 0\]
\[\Rightarrow {{b}^{2}}-4ax\ge 0\]
\[\Rightarrow 1-4{{y}^{2}}\ge 0\]
\[\Rightarrow 4{{y}^{2}}-1\le 0\]
\[\Rightarrow (2y+1)(2y-1)\le 0\]
\[\Rightarrow \frac{-1}{2}\le y\le \frac{1}{2},y\ne 0\]
Hence, range of \[y=\left[ \frac{-1}{2},\frac{1}{2} \right]\]
You need to login to perform this action.
You will be redirected in
3 sec
