3rd Class Mathematics Fractions Fraction

Fraction

 Introduction

The Latin name of fraction is fractus. It means broken. Fractions are always in ratio form. It has two parts, upper and lower part. The upper part is called numerator and lower part is denominator.

Fractions in its Lowest Term

The lowest term of a fraction is obtained by dividing numerator and denominator with common divisor. The lowest form of the fraction  \[\frac{6}{9}\,\,is\,\frac{2}{3}\] . The lowest term of the fraction \[\frac{6}{9}\] is obtained by dividing the numerator and denominator with a common divisor 3.

•            Example

What is lowest term of the fraction\[\frac{\mathbf{45}}{\mathbf{65}}\]?

            (a) \[\frac{9}{13}\]                                                         (b) \[\frac{2}{3}\]

            (c) \[\frac{5}{9}\]                                                                       (d) All the above

            (e) None of these

Ans.     (a)

            Explanation: Common divisor of 45 and 65 is 5. Therefore, dividing 45 and 65 by 5, we get \[\frac{9}{13}\]

•           Example

            Find the simplest form of the shaded parts of the figures in fraction given below:

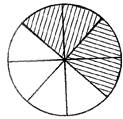
            (a) \[\frac{3}{8}\]                                                                       (b) \[\frac{1}{2}\]           

            (c) \[\frac{1}{5}\]                                                                       (d) All the above

            (e) None of these

Ans.     (b)

            Explanation: Total number of divisions is 8 and number of shaded parts is 4.

            Therefore, shaded parts \[=\frac{4}{8}=\frac{1}{2}\]

Proper, Improper and Mixed Fractions

The fraction whose numerator is smaller than the denominator is called proper fraction. The fractions whose numerator is greater than the denominator is called improper fractions. A mixed fraction has both whole and fractional parts. The fraction

\[3\frac{7}{3}\] is a mixed fraction

•            Example

Which one of the following fractions is correct about the shaded parts of the given figure?

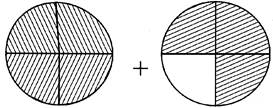
            (a) \[1\frac{3}{4}\]                                                                     (b) \[1\frac{5}{3}\]          

            (c) \[5\frac{3}{4}\]                                                                     (d) All the above

            (e) None of these

Ans.     (a)

            Explanation: Total number of parts in each figure = 4 number of shaded parts in are 4 and 3 respectively.

Therefore, shaded parts \[=\frac{4}{4}+\frac{3}{4}=1+\frac{3}{4}=1\frac{3}{4}\]

Equivalent Fraction

If numerator and denominator of a fraction is multiplied by the same number, the resulting fraction is called its equivalent fraction.

For example, the equivalent fractions of \[\frac{3}{4}\] are \[\frac{3}{4}\times \frac{2}{2}=\frac{6}{8},\,\,\frac{3}{4}\times \frac{3}{3}=\frac{9}{12},\,\,\frac{3}{4}\times \frac{4}{4}=\frac{12}{16}\]

•            Example

Consider the following statements:

Statement 1: Equivalent fraction is obtained by multiplying a number with numerator and denominator

Statement 2: Equivalent fraction is obtained by adding two fractions.

Which one of the following is correct about the above statements?

            (a) Statement 1 is false and 2 is true

            (b) Statement 1 and 2 both are false

            (c) Statement 1 is true and 2 is false

            (d) All the above

            (e) None of these

Ans.     (c)

Ø  Example

What should be multiplied with the fraction \[\frac{\mathbf{3}}{\mathbf{4}}\] to get an equivalent fraction\[\frac{\mathbf{9}}{\mathbf{12}}\]?

            (a) 3                                                                  (b) 4           

            (c) 6                                                                  (d) All the above

            (e) None of these

Ans.     (a)

Points to Remember

Two or more fractions can be added or subtracted if denominator is same in all fractions. Denominator will remain same and number is calculated by simple addition or subtraction.

For example: \[\frac{3}{4}+\frac{2}{4}=\frac{3+2}{4}=\frac{5}{4}\]