4th Class Mathematics Area, Perimeter and Volume Area and Perimeter

LEARNING OBJECTIVES

This lesson will help you to:—

• outline the boundary of a shape.
• identify shapes like square, rectangle and circle and separate it from other shapes.
• explore intensively the area and perimeter of simple shapes.
• estimate the area and perimeter of a shape.
• find the area and perimeter of a shape using grid method.

 

Real Life Examples

• Knowledge of area and perimeter helps in installing a garden.
• The perimeter can be used to calculate the length of fence required to surround a yard or garden.
• The perimeter of a wheel (its circumference) describes how far it will roll in one revolution.
• The amount of string wound around a spool is related to the spool’s perimeter.
• Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape.
• Area is the amount of paint necessary to cover the surface with a single coat.

 

QUICK CONCEPT REVIEW

Diagrams/pictures

Perimeter

1. The distance around the edge of a shape is called boundary or perimeter of the shape. It is always measured in single unit that is cm, m, km etc.

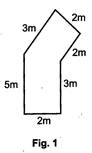
The perimeter of fig. 1 is the total distance around it.

The total distance around the fig. 1

= 3m + 2m + 2m + 3m + 2m + 5m = 17m

\[\therefore \]Perimeter of fig. 1 = 17 m.

Hence, the sum of all the lengths of shape is called its perimeter.

                    

Here, each square is of side 1 unit.

Perimeter of shaded region

= 2 units + 5 units + 4 units + 2 units + 2 units

                                                         + 3 units = 18 units

1. Perimeter of a square is the sum of the length of its sides.

Perimeter of square in fig. 3

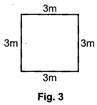
= Sum of the sides of the square

= 3m + 3m + 3m + 3m or

\[=4\times 3m=12m\]

Thus, perimeter of a square = 4 x side

Perimeter of a rectangle is the sum of the length of its sides.

 

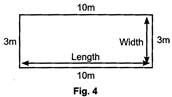
Perimeter of rectangle in fig. 4

= sum of the sides of the rectangle

\[=3m+10m+3m+10m\]or

\[=(3m+3m)+(10m+10m)\]

\[=(2\times 3m)+(2\times 10m)\]

\[=2\times (3m+10m)\]

\[=2\times (13m)=26\text{ }m\]

Thus, perimeter of a rectangle = 2 x (length + width)

Perimeter of a circle is the distance around the circle.

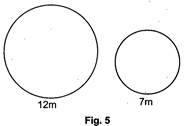
Also, perimeter of a circle is known as circumference of it.

Amazing Facts

• A circle has the shortest perimeter of all shapes with the same area.
• Area and perimeter are two calculations performed on many geometrical shapes. Perimeter is a measure of distance around a shape: for example, someone might want to figure out the perimeter around their garden before buying material to make a fence so that they know how much material to buy. Area is a measure of the amount of surface something covers. For example, someone might want to know how much space their garden takes up.
• Area and perimeter are often grouped together because one can be used to help you figure out the other. For example, if you know the perimeter of a square, you can easily figure out the area, and vice-versa.

Historical Preview

• The first recorded use of areas and perimeters in the West was in ancient Babylon, where they used it to measure the amount of land that was owned by different people for taxation purpose.
• The mathematics of Egyptian geometry is documented by examples of rules for determining areas and volumes of common plane and solid objects. They appear to be based on trial and error results and observations as opposed to theoretical proof.

 

AREA

Area is the total number of square units that fill a given shape.

Area of fig. 6

 

= Total number of squares in the shape

= 26 square units.

When we divide a square into squares of length 1 unit, then we can see that we get same number of squares in rows and columns.

In this case, we can multiply the number of squares in any one row with the number of squares in any one column to get the area of the square.

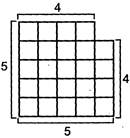
In fig. 7,

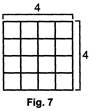
Area of square = (Number of squares in row) x (Number of squares in column)

\[=4\times 4=16\]square units

Thus, area of a square = side\[\times \]side.

When we divide a rectangle in squares of length 1 unit, then we can see that we get more number of squares in either rows or columns. In this case, we can multiply the number of squares in any one row with the number of squares in any one column to get the area of the rectangle.

In fig. 8, the area of rectangle

= (Number of squares in one row)

\[\times \](Number of squares in one column)

\[=7\times 5=\]35 square units

 

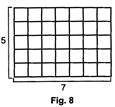
Thus, we have area of rectangle = length x breadth (width)

Note: We can use the formula to measure the area of triangle\[\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ base }\!\!\times\!\!\text{ height}\].

Examples

Suresh bought a mat as given below. He wants to know whether he can spread that mat in his living room.

Let us find the area of the mat.

The mat is divided into squares of length 1m. So, we get 4 squares in each row and 2 squares in each column.

\[\therefore \]The area of mat \[=4\times 2=8\]square metre

Sangeeta aunty bought a new saree for her nephew's wedding. She want to stitch a new matching lace around its boundary.

To find the length of the lace required to stitch around the boundary of the saree, we need to find its perimeter.

Perimeter of saree = 5m + 2m + 5m + 2m = 14 m

Thus, 14m lace is required for the saree.

 

Shortcut to problem solving

• To find the perimeter of different figures, we can use certain formulae.

Perimeter of a square

\[=4\times \text{side}\]

Perimeter of rectangle

= 3 (length + breadth).

Perimeter of a triangle

= a + b + c.

where a, b, c are the sides of the triangle.

• To, find the area of different figures, we can use certain formulae.

Area of a square

= side\[\times \]side

Area of rectangle

=Length\[\times \]breadth.

Area of a triangle

\[\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ base }\!\!\times\!\!\text{ height}\]

Misconcept/Concept

Misconcept: When a unit square is removed from a given shape then both its area and perimeter get reduced by square unit and a unit respectively.

Concept: When a unit square is removed from a given shape then its area gets reduced by a square unit but its perimeter either remains same or gets increased by few units.

Note: Example for the concept is elaborated for you after flow chart.

For example: Consider the square given below divided into unit squares.

Perimeter = 5 + 5 + 5 + 5

= 20 units

Area \[=5\times 5=25\]square units.

(i) Let us now remove a square unit from it and then calculate the area and perimeter of the whole square.

 

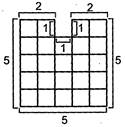
Perimeter = 5 + 5 + 5 + 2 + 1 + 1 + 1 + 2

= 22 units                           

Area = 24 square units.                         

(ii) Let us now remove a square unit from the corner and then calculated the area and perimeter of the whole square.

 

Perimeter = 4 + 1 + 1 + 4 + 5 + 5            

= 20 units                    

Area = 24 square units.                     

Thus, we can see that when we remove unit square from a shape then its area gets reduced by a square unit and its perimeter either remains the same or gets increased by few units.