Perimeter
Category : 4th Class
As you know all the geometrical shapes like triangles, quadrilaterals, etc. occupy some area. Perimetre is referred as the length of the boundary line which subtend the area. In the rectilinear figure the area is bounded by the line segments are called sides. Thus perimetre can be referred as the sum of the length of the total sides.
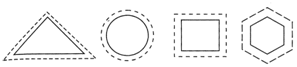
Dotted line in the above figures shows perimetre.
![]() Perimetre of the Triangles
Perimetre of the Triangles
Triangle is a one of the most simple shape of geometry which is made up of three sides. So to find the perimetre of the triangle we add length of all the three sides of the triangle.
Thus, perimetre of a triangle = Sum of length of all three sides.
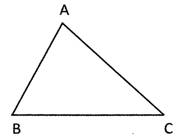
Perimetre of the triangle \[\text{ABC}=\text{AB}+\text{BC}+\text{CA}\]
![]()
Find the perimetre of the given triangle.
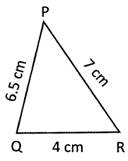
Solution:
Perimetre of the triangle \[\text{PQR=PQ}+\text{QR}+\text{RP}\] \[=\text{6}.\text{5 cm}+\text{4 cm}+\text{7 cm}=\text{17}.\text{5 cm}\]
![]() Perimetre of an Equilateral Triangle
Perimetre of an Equilateral Triangle
All three sides of an equilateral triangle are equal so to find the perimetre of a triangle we multiply the length of one side of the triangle by 3. Thus, perimetre of an equilateral triangle \[=\text{3}\times \text{side}\]
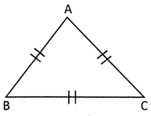
Perimetre of the triangle \[\text{ABC}=\text{3}\times \text{AB}\]
![]()
Find the perimetre of the triangle PQR.
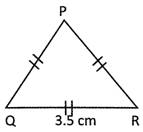
Solution:
Perimetre of an equilateral triangle \[=\text{3}\times \text{side}\]
In the triangle PQR Perimetre of the triangle \[~\text{PQR}=\text{3}\times \text{PQ}\] \[=\text{3}\times \text{3}.\text{5 cm}=\text{1}0.\text{5 cm}\]
![]() Perimeter of an Isosceles
Perimeter of an Isosceles
Triangle An isosceles triangle has two equal sides. So to find the perimetre of an isosceles triangle, we multiply length of one of the equal sides by 2 then add the length of third side. Thus perimetre of an isosceles triangle \[=\text{2}\times \] length ofone of the equal sides + length of the third (unequal) side
Perimetre of the triangle \[\text{ABC}=\text{2}\times \text{AB}+\text{BC}\]
![]()
Find the perimetre of the triangle PQR.
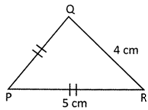
Solution:
Perimetre of an isosceles triangle\[=2\times \text{length}\] of one of the equal sides + length of unequal side In the triangle PQR Perimeter of the triangle \[\text{PQR}=\text{2}\times \text{PQ}+\text{QR}=\text{2}\times \text{5 cm}+\text{4 cm}=\]\[\text{14 cm}\]
![]() Perimeter of an Scalene
Perimeter of an Scalene
Triangle In an scalene triangle all three sides are of different length. So to find the perimeter of an scalene triangle we add the length of all the three sides.
Perimeter of an scalene triangle = Length of first side + Length of second side + Length of third side
Perimetre of the triangle \[\text{PQR}=\text{PQ}+\text{QR}+\text{RP}\]
![]()
Find the perimetre of the given triangle.
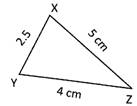
Solution:
Perimeter of an scalene triangle = Sum of the length of all sides. In triangle XYZ Perimetre of the triangle XYZ \[=xy+yz+zx=\text{2}.\text{5 cm}+\text{4 cm}+\text{5 cm}=\text{11}.\text{5}\]cm.
![]() Perimeter of the Quadrilaterals
Perimeter of the Quadrilaterals
A quadrilateral is made up of four sides. So to find the perimeter of a quadrilateral we add the length of all sides.
Thus perimeter of a quadrilateral = Sum of the length of all sides.
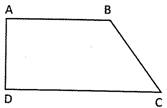
Perimeter of the quadrilateral \[\text{ABCD}=\text{AB}+\text{BC}\]\[+\text{CD}+\text{DA}\]
![]()
Find the perimeter of the given quadrilateral.
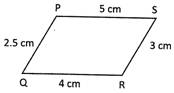
Solution:
Perimeter of the quadrilateral PQRS \[=\text{PQ}+\text{QR}+\text{RS}+\text{SP}=\text{2}.\text{5 cm}+\text{4 cm}+\text{3 cm}+\text{5}\]\[\text{cm}=\text{14}.\text{5 cm}\]
![]() Perimeter of a Rectangle
Perimeter of a Rectangle
Rectangle is a quadrilateral which has equal opposite sides. So to find the perimeter of a rectangle sum of length and breadth of the rectangle is multiplied by 2. perimeter of a rectangle = 2 (Length + Breadth)
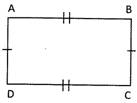
Perimeter of the rectangle ABCD = 2(AB + BC)
![]()
Find the perimeter of the given rectangle.
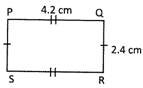
Solution:
Perimeter of the rectangle \[\text{PQRS}=\text{2(PQ+QR)}\] \[=\text{2(4}.\text{2 cm}+\text{2}.\text{4 cm)=13}.\text{2 cm}\].
![]() Perimeter of a Square
Perimeter of a Square
Square is a quadrilateral which has all equal sides. So to find the perimeter of a square we multiply the length of one side of a square by 4. Thus, perimeter of a square\[=\text{4}\times \text{length}\]of one side of the square
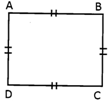
Perimeter of the square\[\text{ABCD}=\text{4}\times \text{AB}\]
![]()
Find the perimeter of the given square.
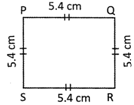
Solution:
Perimeter of the square \[~\text{PQRS}=\text{4}\times \text{PQ}=\text{4}\times \]\[\text{5}.\text{4 cm}=\text{21}.\text{6 cm}\]
![]() Perimeter of a Circle
Perimeter of a Circle
Circle is a geometrical shape which is made up of a curved line. To find the perimeter of a circle, diameter of the circle is multiplied by a constant \[\pi \]. Thus, perimeter of a circle \[=\pi \times \text{diameter}\] Or perimeter of a circle \[=\pi \times \text{2}\times \text{radius}\] (Diameter\[=\text{2}\times \text{radius}\] )
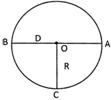
Perimeter of the circle \[=\pi \,d\] Or perimeter of the circle\[=2\pi \,r\]
![]()
Find the perimeter of a circle whose radius is 11.2 cm.
Solution:
Perimeter the circle \[=\text{2}\times \frac{22}{7}\times \text{11}.\text{2}\] cm = 70.4 cm
![]()


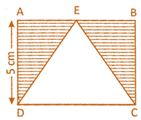
![]() ABCD is a square. Find the area of the shaded part in the following figure:
ABCD is a square. Find the area of the shaded part in the following figure:
(a)\[\text{12c}{{\text{m}}^{\text{2}}}\]
(b) \[\text{12}.\text{5c}{{\text{m}}^{\text{2}}}\]
(c)\[\text{25c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{11}.\text{5}\,\text{c}{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer (b)
Explanation
Area of the square\[\text{ABCD}=\text{5cm}\times \]\[5\,cm=25\,c{{m}^{2}}\]
Area of the triangle \[\text{CDE}=\frac{1}{2}\times 5cm\times 5cm=12.5\,c{{m}^{2}}\]
Area of the shaded part = Area of the square ABCD - Area of the triangle \[\text{CDE}=\text{25 c}{{\text{m}}^{\text{2}}}-\text{12}.\text{5 c}{{\text{m}}^{\text{2}}}=\text{12}.\text{5 c}{{\text{m}}^{\text{2}}}\]
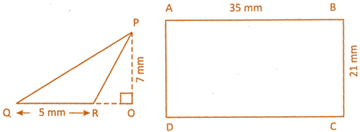
![]() How many triangle PQR can be placed inside the rectangle ABCD?
How many triangle PQR can be placed inside the rectangle ABCD?
(a) 42
(b) 40
(c) 44
(d) 38
(e) None of these
Answer (a)
Explanations
Area of the triangle \[\text{PQR}=\frac{1}{2}\times \text{5mm}\times \text{7mm}=\]\[\text{17}.\text{5 m}{{\text{m}}^{\text{2}}}\]
Area of the rectangle \[\text{ABCD}=\text{35 mm}\times \text{21 mm}\]\[=\text{735 m}{{\text{m}}^{\text{2}}}\]
Let X triangles can be placed inside the rectangle ABCD Thus \[17.5\,m{{m}^{2}}\times X=735\,m{{m}^{2}}\] \[X=\frac{735\,m{{m}^{2}}}{17.5\,m{{m}^{2}}}=42\]
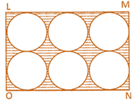
![]() LMNO is a rectangle whose length is 16.8 cm and breadth is 11.2cm. Inside the rectangle LMNO there are 6 equal circles. Find the area of shaded region.
LMNO is a rectangle whose length is 16.8 cm and breadth is 11.2cm. Inside the rectangle LMNO there are 6 equal circles. Find the area of shaded region.
(a)\[\text{4}0.\text{36}\,\text{c}{{\text{m}}^{\text{2}}}\]
(b) \[\text{36}.\text{4}0\,\text{c}{{\text{m}}^{\text{2}}}\]
(c)\[\text{32}.\text{4}0\,\text{c}{{\text{m}}^{\text{2}}}\]
(d) \[\text{4}0.\text{32}\,\text{c}{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer (d)
![]() Area of a triangle is \[~\text{9}0\text{ c}{{\text{m}}^{\text{2}}}\]. Find the height of the triangle, if the base of the triangle is 5 cm.
Area of a triangle is \[~\text{9}0\text{ c}{{\text{m}}^{\text{2}}}\]. Find the height of the triangle, if the base of the triangle is 5 cm.
(a) 9cm
(b) 12cm
(c) 36cm
(d) 24cm
(e) None of these
Answers (c)
![]() Area of a rectangular park is \[\text{99}0\text{ }{{\text{m}}^{\text{2}}}\]. If breadth of the park is 22 m, find the length of the park.
Area of a rectangular park is \[\text{99}0\text{ }{{\text{m}}^{\text{2}}}\]. If breadth of the park is 22 m, find the length of the park.
(a) 40m
(b) 45m
(c) 50m
(d) 55m
(e) None of these
Answer (b)
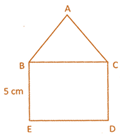
![]() In the given figure, BCDE is a square and ABC is an equilateral triangle. Find the perimeter of the following figure:
In the given figure, BCDE is a square and ABC is an equilateral triangle. Find the perimeter of the following figure:
(a) 35cm
(b) 30cm
(c) 25cm
(d) 20cm
(e) None of these
Answer (b)
Expiations
Perimeter of the figure \[=\text{AB}+\text{BE}+\]\[\text{ED}+\text{DC}+\text{CA}\]\[\because \] BCDE is asquare and ABC is an equilateral triangle\[\therefore \]\[\text{AB}=\text{BE}=\text{ED}=\text{DC}=\text{CA}=\text{5 cm}\] Thus, perimetre of the figure \[=\text{5cm}+\text{5cm}+\text{5}\]\[\text{cm}+\text{5cm}+\text{5cm}=\text{25cm}\]
![]() Area of an equilateral triangle is\[\text{24 c}{{\text{m}}^{\text{2}}}\]. If height of the triangle is 8 cm, find the perimetre of the triangle.
Area of an equilateral triangle is\[\text{24 c}{{\text{m}}^{\text{2}}}\]. If height of the triangle is 8 cm, find the perimetre of the triangle.
(a) 9cm
(b) 18 cm
(c) 27 cm
(d) 36 cm
(e) None of these
Answer (b)
Explanations-
Area of the triangle \[=\text{24}\,\text{c}{{\text{m}}^{\text{2}}}\frac{1}{2}\times Base\times 8cm=24c{{m}^{2}}\] \[Base=\frac{48\,c{{m}^{2}}}{8\,cm}Base=6\,cm\] Thus, perimetre of the equilateral triangle \[=\text{3}\times \text{6cm}=\text{18 cm}\]
![]() Find the perimetre of an isosceles triangle whose length of unequal side is 5 cm which is 3 cm less than the sum of the length of equal sides.
Find the perimetre of an isosceles triangle whose length of unequal side is 5 cm which is 3 cm less than the sum of the length of equal sides.
(a) 5cm
(b) 8cm
(c) 21cm
(d) 13cm
(e) None of these
Answer (d)
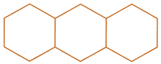
![]() In the following figure, there are three equal hexagons whose each side is equal. If length of one equal side is 3 cm, find the perimeter of the figure.
In the following figure, there are three equal hexagons whose each side is equal. If length of one equal side is 3 cm, find the perimeter of the figure.
(a) 54cm
(b) 48cm
(c) 42cm
(d) 36cm
(e) None of these
Answers (c)
![]() ABC is a scalene triangle whose perimetre is 49 cm. In which AB is 2 cm greater than BC and 3 cm lesser than AC. Find the longest side of the triangle ABC.
ABC is a scalene triangle whose perimetre is 49 cm. In which AB is 2 cm greater than BC and 3 cm lesser than AC. Find the longest side of the triangle ABC.
(a) 14cm
(b) 16cm
(c) 19cm
(d) 23cm
(e) None of these
Answers (c)
You need to login to perform this action.
You will be redirected in
3 sec
