Fractions
Category : 4th Class
Fractions
Synopsis
Fraction:
e.g., ![]()
Like fractions: Fractions which have a common denominator are called like fraction
e.g., \[\frac{2}{9},\frac{4}{9},\frac{5}{9}\]etc.,
Unlike fractions: Fractions with different denominators are called unlike fraction;
e.g., \[\frac{2}{3},\frac{4}{5}\]
Proper fraction: In a fraction, if the numerator is less than the denominator, it I called a proper fraction.
e.g., \[\frac{2}{5},\frac{7}{11}\]etc.,
Improper fraction: In a fraction, if the numerator is greater than or equal to the denominator it is called an improper fraction.
|
Note: if the numerator is equal to the denominator, the fraction represents a whole number, i.e., 1 |
Unit fractions: Fractions with 1 or unity as the numerator are called unit fractions
e.g., \[\frac{1}{3},\frac{1}{5}\]etc.,
Mixed fraction: A fraction which is a combination of a whole number and a fraction is called a mixed fraction or mixed number
e.g., \[1\frac{3}{4},7\frac{1}{11}\]
Equivalent fractions: The fractions that represent the same part are called equivalent fractions.
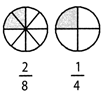
Both \[\frac{2}{8}\] and \[\frac{1}{4}\] represent the same part of a whole. So \[\frac{2}{8}=\frac{1}{4}\].
Comparing fractions:
(a) Fractions with the same numerators: Of two fractions with a common numerator, the fraction that has a smaller denominator is greater.
e.g., \[\frac{3}{5}\]and \[\frac{3}{7}\]
Since, the numerators are the same, comparing their denominators, we get \[\text{5}<\text{7}\].
\[\therefore \] \[\frac{3}{5}>\frac{3}{7}\]
(b) Fractions with the same denominators: Of two fractions with a common denominator, the fraction that has a larger numerator is greater
e.g., \[\frac{2}{9}\]and \[\frac{7}{9}\]
Since the denominators are the same, comparing their numerators, we get \[7>2\].
\[\therefore \] \[\frac{7}{9}>\frac{2}{9}\]
(c) Fractions with different numerators and denominators: To compare fractions with different numerators and denominators, first convert them to get the same denominator by writing their equivalent fractions and then compare.
e.g., \[\frac{3}{4}\] and \[\frac{5}{6}\]
Step 1: Check if numerators or denominators are the same. The given fractions do not have the same numerators or denominators.
Step 2: Find equivalent fractions with common denominators. \[\frac{3\times 3}{4\times 3}=\frac{9}{12}\] and \[\frac{5\times 2}{6\times 2}=\frac{10}{12}\]
Step 3: Compare the numerators. \[\text{9}<\text{1}0\]
\[\therefore \]\[\frac{3}{4}<\frac{5}{6}\]
Ordering fractions: Writing fractions in ascending or descending orders is called ordering fractions.
e.g., 1: The fractions\[\frac{1}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\]and \[\frac{6}{7}\]are in ascending order since\[\text{1}<\text{3}<\text{4}<\text{5}<\text{ 6}\].
e.g., 2: The fractions \[\frac{8}{9},\frac{7}{9},\frac{6}{9},\frac{5}{9}\]and\[\frac{2}{9}\]are in descending order since\[\text{8}>\text{7}>\text{6}>\text{5}>\text{2}\].
Addition of fractions: To add two like fractions,
(a) Add the numerators,
(b) Write the sum over the same denominator.
Subtraction of fractions: To subtract two like fractions,
(a) Subtract the numerators,
(b) Write their difference over the same denominator.
e.g., \[\frac{8}{9}-\frac{3}{9}=\frac{8-3}{9}=\frac{5}{9}\]
Fraction of a number: To find the fraction of a number,
(a) Divide the number by the denominator.
(b) Multiply the quotient obtained by the numerator.
e.g., \[\frac{3}{4}\]of \[60.\]\[60\div 4=15\]and \[3\times 15=45\Rightarrow \frac{3}{4}\]of \[60=45\]
Conversions:
(a) Converting a mixed fraction into an improper fraction:
(i) Multiply the whole number by the denominator.
(ii) Add the numerator to the product obtained.
(iii) Write the sum over the denominator.
e.g., \[3\frac{1}{2}=\frac{3\times 2+1}{2}=\frac{7}{2}\]
(b) Converting an improper fraction into a mixed number:
(i) Divide the numerator by the denominator.
(ii) Write the quotient as the whole number part of the mixed fraction.
(iii) Write the remainder as the numerator over the same denominator beside the whole number.
e.g., ![]()
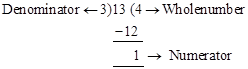
![]()
![]()
|
Note: The denominator of improper fraction and its mixed fraction are the same.. |
You need to login to perform this action.
You will be redirected in
3 sec
