4th Class Mathematics Multiplication and Division Multiplications and Division

Multiplications and Division

Synopsis

1. Multiplication:

• Multiplication is repeated addition of the same number.

e.g., \[\text{15}+\text{ 15 }+\text{ 15 }+\text{ 15 }=\text{ 4}\times \text{15}\]

• In a multiplication, the number that is multiplied is called multiplicand, the number by which it is multiplied is called multiplier and the answer obtained is called result or

Properties of multiplication:

(a) Changing the order of numbers to be multiplied does not change their product.

e.g., \[\text{5}\times \text{9}=\text{ 45 }=\text{9}\times \text{5}\]

(b) The product of any number and 0 is 0.

e.g., \[~\text{43}\times 0=0\]

(c) The product of any number and 1 is the number itself.

e.g., \[~\text{59}\times \text{1}=\text{59}\]

(d) The product of a number and the sum of two numbers is equal to the sum of the products with the two numbers separately.

e.g., \[\text{4}\times (\text{3 }+\text{ 6})=\text{4}\times \text{9}=\text{36}\]

\[\therefore \] \[\text{4}\times (\text{3}+\text{6})=\text{4 }\times \text{ 3}+\text{4 }\times \text{ 6}=\text{12}+\text{24}=\text{36}\]

(e)  To multiply a number by \[\text{1}0,\text{ 2}0,\text{ }.....\text{ 9}0,\] first multiply the number by \[\text{1},\text{ 2},\text{ }...\text{ 9}\]respectively and place a zero to the right of the product.

e.g., \[\text{146 }\times \text{ 2}0=\text{146 }\times \text{ 2 }\times \text{ 1}0=\text{292 }\times \text{ 1}0=\text{292}0\](f) To multiply a number by \[\text{1}00,\text{2}00,\text{3}00,\text{ }....,\text{9}00,\] first multiply the number with \[\text{1},\text{2},\text{3},\text{ }....,\text{9}\]and place two zeroes to the right of the product.

e.g., \[~\text{456 }\times \text{ 1}00\text{ }=\text{ 456 }\times \text{ 1 }\times \text{ 1}00\text{ }=\text{ 456}00\]

(g)  To multiply a number by \[\text{1}000,\text{2}000,\text{3}000\]etc., first multiply the number by \[\text{1},\text{2},\text{3},\text{ }....,\text{9}\] and place three zeroes to the right of the product.

e.g., \[\text{497 }\times \text{ 1}000=\text{497}00\]

1. Division:

• Division is repeated subtraction of the same number.

e.g., \[\text{15}-\text{3}=\text{12};\] \[\text{12}-\text{3}=\text{9};\] \[\text{9}-\text{3}=\text{6};\]\[\text{6}-\text{3}=\text{3};\]  \[\text{3}-\text{3}=0\]

• Division is also a process of equal distribution.

e.g., 15 chocolates are to be distributed equally among 5 children.

Each child gets 3 Chocolates.

            \[\therefore 15\div 5=3\]

• In a division, the number to be divided is called dividend, the number that divides is called divisor, the answer obtained is called quotient and the left over number is called remainder.

e.g.,           Dividend

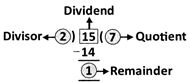
Properties of division:

(a) When a number except 0 is divided by itself the quotient is 1.

e.g., \[45\div 45=1\]

(b) When a number is divided by 1, the quotient is the number itself.

e.g., \[\text{57}-\text{1}=\text{57}\]

(c) When zero is divided by any number (except 0), the quotient is 0.

e.g., \[~0-\text{18}=0\]

(d)  Divison by zero is not possible.

(e) When a number is divided by 10, the quotient is the dividend written without the ones digit, while the ones digit is the remainder.

e.g.,    (1) \[\text{1}00\div \text{1}0=\text{10 R 0}\]

            (2) \[\text{54}\div \text{1}0=\text{5 R 4}\]

(f)  When a number is divided by 100, the quotient is the dividend written without the tens and ones digits, while the remainder is the number formed by the tens and ones digits taken together.

e.g.,   (1) \[\text{4395}\div \text{1}00=\text{43 R 95}\]

            (2) \[\text{34}00\div \text{1}00\text{ }=\text{ 34 R }0\]

(g) When a number is divided by 1000, the quotient is the dividend written without the ones, tens and hundreds digits, while the remainder is the number formed by the hundreds, tens and ones digits taken together.

e.g.,    (1) \[\text{64823}\div \text{1}000=\text{64 R 823}\]    

(2) \[\text{82}000\div \text{1}000=\text{82 R }00\]

• In any division, the relation given in the box holds good.

\[\mathbf{Dividend = Quotient }\times \mathbf{ Divisor + Remainder}\]This relation is used to check the correctness of division problems.

Estimating products and Quotients:

(a) Estimating products

Estimation is done by considering numbers close to the original numbers.

e.g., Find the product of 63 and 42.

Method 1: Estimate as per rules of rounding.

63 rounds to 60; 42 rounds to 40

\[\therefore \]    \[\text{6}0\times \text{4}0=\text{24}00\]

Actual product:

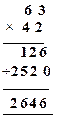
Method 2:

Round one number up and the other number down.

\[63\to 65;42\to 0\]

Their product is \[\text{65 }\times \text{ 4}0\text{ }=\text{ 26}00.\]

Note: 1. Method 2 gives a better estimate of the product.

2. In large numbers rounding to the nearest 10 gives a better estimate than rounding to this nearest 100.

(b) Estimating quotients:

When dividing by a 2- digit number, it is useful to first estimate the quotient.

e.g., \[73\div 28\]rounds to \[70\div 30\]which gives a quotient 2.

Note: While estimating quotients, ignore the remainder. Rounding a 3- digit dividend to the nearest 10 gives a better estimate than rounding it to the nearest 100.