Division of a Decimal by the Power of 10
Category : 5th Class
Step 1: Shift the point in the decimal left as many places as the number of zeroes the power of 10 contains.
Step 2: If there are short of digits left to the point in the decimal, add zeroes left to it and follow the step 1.
![]()
Divide 256.52 by 100.
Explanation
100 contains two zeroes, therefore, shift the point two digit left in the decimal
Thus \[256.52\div 100=2.5652\text{ }.\]
![]()
Divide 3.25 by 10000.
Explanation
10000 contains 4 zeroes and 3.25 has only 1 digit left to the point so add ; zeroes left to it and shift the decimal 4 places left.
Thus \[3.25\div 10000=0.000325.\]
![]() Division of a Decimal by a Whole Number
Division of a Decimal by a Whole Number
Step 1: Remove the point from the decimal and divide it by the whole number.
Step 2: Shift the point left in the quotient as many places as the given decimal has total number of digits right to the point.
Step 3: If the quotient is a whole number then insert a point in it so that it has equal number of decimal places as the given 'decimal has.
or
Step 1: Convert the decimal into fraction.
Step 2: Divide the fraction by the whole number.
![]()
Divide 45.25 by 8
Solution:
Write the decimal without point and divide it by the whole number
Thus \[4525\div 88=565.625\]
The given decimal 45.25 has two digit right to the point, therefore, shift the decimal two digit left.
Thus \[45.25\div 8=5.65625.\]
Or
\[45.25=\frac{4525}{100}\]
Thus \[45.25\div 8=\frac{4525}{100}\div =\frac{4525}{100}\times \frac{1}{8}\]
Or \[\frac{4525}{8}\times \frac{1}{100}=565.625\times \frac{1}{100}=5.65625\]
![]() Division of a Whole Number by a Decimal
Division of a Whole Number by a Decimal
Step 1: Remove the point from the decimal.
Step 2: Divide the whole number by the obtained number in the first step.
Step 3: Multiply the quotient by 10 if there are one digit right to the point in the given decimal, by 100 if there are two digit right to the point in the given decimal and so on.
or
Step 1: Convert the decimal into fraction.
Step 2: Divide the whole number by the fraction.
![]()
Divide 910 by 3.5.
Explanation
Remove the point from the decimal and divide the whole number by it
Thus\[910\div 35=26\]
The decimal 3.5 contains only one digit right to the point, so multiply the quotient by 10
Thus \[910\div 3.5=260.\]
Or
\[3.5=\frac{35}{10}\]
Thus \[910\div 3.5=910\div \frac{35}{10}\]
\[910\times \frac{10}{35}\]
\[=\frac{910\times 10}{35}=260\]
![]() Division of Decimals
Division of Decimals
Step 1: Multiply the dividend and divisor by a power of 10 (like 10,100,1000 etc.) so that divisor becomes a whole number.
Step 2: Follow the steps given for division of a decimal by a whole number.
or
Step 1: Convert the decimals into fractions.
Step 2: Divide the fraction by divisor fraction.
![]()
Divide 15.504 by 3.4.
Explanation
The divisor decimal 3.4 contains one digit right to the point so it requires to be multiplied with 10 to convert into a whole number. Therefore, we have to multiply both divisor and dividend by 10
Thus \[3.4\times 10=34\] and \[15.504\times 10=155.04\]
Explanation
Now divide 155.04 by 34
\[155.04\div 34=4.56\]
\[3.4\frac{34}{10},15.504=\frac{15504}{1000}\]
Thus \[155.04\div 34=\frac{15504}{1000}\div \frac{34}{10}\]
\[\frac{15504}{1000}\times \frac{10}{34}=\frac{15504}{34}\times \frac{1}{100}\]
\[456\times \frac{1}{100}=4.56\]

![]()

![]() What decimal should be added to 15.236 to get the sum 15.281?
What decimal should be added to 15.236 to get the sum 15.281?
(a) 10.045
(b) 10.45
(c) 0.045
(d) 10.25
(e) None of these
Answer: (c)
Explanation
Let \[x\] should be added to 15.236 to get 15.281
Thus \[\text{15}\text{.236 +X=15}\text{.281}\]
\[\text{X= 15}\text{.281-15}\text{.236}\]
=0.045
![]() Which one of the following digits will come in the extreme right to the sum of\[4.235+56.230+45+2.02+0.02316?\]
Which one of the following digits will come in the extreme right to the sum of\[4.235+56.230+45+2.02+0.02316?\]
(a) 6
(b) 8
(c) 3
(d) 0
(e) None of these
Answer: (a)
Explanation
\[4.235+56.230+45+2.02+0.02316=107.50816\]
![]() What least number should be subtracted from 23.56 so that position of the digits in decimal part gets interchanged?
What least number should be subtracted from 23.56 so that position of the digits in decimal part gets interchanged?
(a) 1.09
(b) 0.91
(c) 0.1
(d) 0.65
(e) None of these
Answer: (b)
![]() What least number should be added to 23.65 so that it becomes 456.32?
What least number should be added to 23.65 so that it becomes 456.32?
(a) 432.67
(b) 479.97
(c) 452.47
(d) 477.57
(e) None of these
Answer: (a)
![]() Line bought a second hand car for Rs 976.75 and her overhead expense was Rs 50.25. She sold it for Rs 1037.75 what was her gain or loss?
Line bought a second hand car for Rs 976.75 and her overhead expense was Rs 50.25. She sold it for Rs 1037.75 what was her gain or loss?
(a) Rs 10 loss
(b) Rs 15 loss
(c) Rs 10 gain
(d) Rs 15 gain
(e)None of these
Answer: (e)
![]() \[5.62\times 36.3\times 0.3,\]find the digit that is at the ten thousandths place in the product.
\[5.62\times 36.3\times 0.3,\]find the digit that is at the ten thousandths place in the product.
(a) 0
(b) 8
(c) 5
(d) 4
(e) None of these
Answer: (b)
Explanation
\[5.62\times 36.3\times 0.3=61.2018\]
8 is at the ten thousandths place in the product.
![]() Madhu gets Rs 3.75 and Srinu gets Rs 4.25 every day as pocket money. In 7 days, how much more money does Srinu get than Madhu?
Madhu gets Rs 3.75 and Srinu gets Rs 4.25 every day as pocket money. In 7 days, how much more money does Srinu get than Madhu?
(a) Rs 0.50
(b) Rs 3.50
(c) Rs 4.50
(d) Rs 7.50
(e) None of these
Answer: (b)
Explanation
Total money which Madhu gets in 7 days \[\text{=Rs}\,\text{3}\text{.75 }\!\!\times\!\!\text{ 7}\]
26.25\[\text{=Rs}\,26.25\]
Total money which Srinu gets in 7 days \[\text{=Rs}\,\text{4}\text{.25 }\!\!\times\!\!\text{ 7}\]
\[\text{=Rs}\,29.75\]
Difference of the money
\[\text{ }\!\!~\!\!\text{ =Rs29}\text{.75-Rs}\,\text{26}\text{.25=3}\text{.50}\]
![]() Which one of the following is the product of 54 and 45.26?
Which one of the following is the product of 54 and 45.26?
(a) 244.604
(b) 2444.04
(c) 240.0444
(d) 246.44
(e) None of these
Answer: (b)
![]() Find the area of a rectangle whose length is 1.235 m and width is 0.73 m.
Find the area of a rectangle whose length is 1.235 m and width is 0.73 m.
(a) 0.90155
(b) 09.0155
(c) 090.155
(d) 0901.55
(e) None of these
Answer: (a)
![]() 0.10 is divided by 100000. Find the place value of 1 in the quotient.
0.10 is divided by 100000. Find the place value of 1 in the quotient.
(a)\[\frac{1}{10000~}\]
(b)\[\frac{1}{100000}\]
(c) \[\frac{1}{1000000}\]
(d) \[\frac{1}{10}\]
(e) None of these
Answer: (c)
Explanation
\[0.1\div 100000=0.000001.\]
Thus place value of 1 in the quotient \[=\frac{1}{1000000}.\]
![]() The decimal representation of shaded boxes is:
The decimal representation of shaded boxes is:
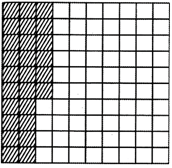
(a) 0.26
(b) 2.6
(c) 26.0
(d) 2600.0
(e) None of these
Answer: (a)
Explanation
There are 100 boxes in the given figure and out of which 26 are shaded
Thus fractional representation for the shaded part \[=\frac{26}{100}\]and \[\frac{26}{100}=0.26.\]
![]() Area of a rectangle is \[\text{1}.\text{7952 k}{{\text{m}}^{\text{2}}}\] . If breadth of the rectangle is 0.24 km, find the length of the rectangle.
Area of a rectangle is \[\text{1}.\text{7952 k}{{\text{m}}^{\text{2}}}\] . If breadth of the rectangle is 0.24 km, find the length of the rectangle.
(a) 7.48km
(b) 7.50km
(c) 6.48km
(d) 8.46km
(e) None of these
Answer: (a)
![]() Find the sum of 32.45 and 78.23.
Find the sum of 32.45 and 78.23.
(a) 120.68
(b) 110.68
(c) 114.68
(d) 130.68
(e) None of these
Answer: (b)
![]() Find the difference between 456.5 and 36. 32
Find the difference between 456.5 and 36. 32
(a) 420.18
(b) 520.18
(c) 620.18
(d) 720.18
(e) None of these
Answer: (a)
![]() Find the product of 32.7 and 24.2.
Find the product of 32.7 and 24.2.
(a) 420.18
(b) 520.18
(c) 620.18
(d) 791.34
(e) None of these
Answer: (d)
You need to login to perform this action.
You will be redirected in
3 sec
