Fraction and its Operations
Category : 7th Class
We have already studied about different kinds of fraction and its properties. In this chapter we will study about some complex problems related to fractions.
Fractional number is defined as a part of whole.
It is represented as \[\frac{p}{q}\] where p & q are the integers and \[p\ne \]0
Here "p" is called the numerator & "q" is called the denominator of the rational number.
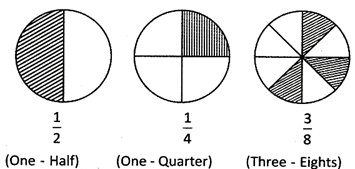
There are three circles given below showing the shaded parts of the circle. \[\frac{1}{2}\]of the circle is half of the whole circle, \[\frac{1}{4}\] of the circle is quarter (fourth) of the whole circle and \[\frac{3}{8}\] of the circle is three- eighth part of the whole circle.
![]() Equivalent Fraction
Equivalent Fraction
Some fractions may look different, but they are equal and therefore, they are called equivalent fractions. It is obtained by multiplying its numerator and denominator by a non - zero numbers. Suppose \[\frac{a}{b}\] be a fraction (where a and b are co-prime and \[b\ne 0),\]then the equivalent fraction is: \[\frac{a}{b},\frac{2\times a}{2\times b},\frac{12\times a}{12\times b},\frac{23a}{23b},\frac{1202\times a}{1202\times b}\]
After reducing the above, we get the result as \[\frac{a}{b}\]
![]()
Rocky merry and John want to divide a chocolate equally among themselves when only two of them are present there. Find their respective share and also find the share of chocolate taken by the girls.
Solution:
The chocolate is divided into three parts given by \[=\frac{1}{3}\] of whole chocolate.
There are two girls in the group, so the share of both the girls \[=\frac{2}{3}\] part of the chocolate.
![]() Properties of Fraction
Properties of Fraction
Property I
Multiplication by the same number with numerator and denominator of the fraction results the same fraction, i.e. \[\frac{a}{b}=\frac{a\times c}{b\times c}\] (Where, a, b and c are integers and \[c\ne 0)\] Shaded part of the circle given below are half \[\left( \frac{1}{2} \right)\]of the circle and they are equal to \[\frac{2}{4}\And \frac{3}{6},\] But ^V are ^P1^^11111^ half of the circle. Therefore, \[=\frac{2}{4}=\frac{3}{6}.\]
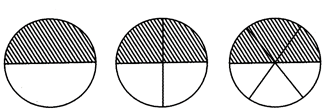
The above given figures represents half of the circle in different ways.
Property II
For every two fractions with equal denominators, the larger fraction is the fraction with the larger numerator.
\[\frac{a}{c}>\frac{b}{c}if\,a>b.\](Where a, b and c are integers and\[c\ne 0)\]
Property III
For every two fraction with equal numerators, the larger fraction is the fraction with the smaller denominator.
\[\frac{a}{b}>\frac{a}{c},\]if \[b<c\](Where a, b and c are integers and c is not equal to 0)
![]() Comparison of the Fraction
Comparison of the Fraction
Sometime we need to compare two fractions to find which is larger or smaller. The following are ways to compare fractions: Decimal Method of Comparing Fractions The method to compare two fractions after converting it into decimal is called decimal method of comparing fractions. It is more clear from the example given below:
![]()
Find the greater fraction: \[\frac{3}{8}\]or \[\frac{5}{12}.\]
Solution:
\[\frac{3}{8}=0.375\And \frac{5}{12}=0.4166\]
Therefore, \[\frac{5}{12}>\frac{3}{8}\]
Comparison of Fraction by Comparing its Denominator
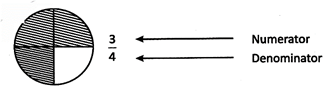
The denominator is the bottom number in a fraction.
It shows how many equal parts the number is to be divided.
If two fractions have the same denominator then they are easy to compare:
If two fraction have unequal denominator then convert them into like fractions.
![]()
Which one is greater \[\frac{4}{9}or\frac{5}{9}?\]
Solution:
Denominator of both the fractions is equal therefore, the number which have greater numerator is greater than other, hence \[\frac{4}{9}<\frac{5}{9}.\]
![]()
Which one is greater: \[\frac{3}{8}or\frac{5}{12}\]
Solution:
Given fractions have unequal denominators. Therefore, its denominator must be equated by multiplying the denominators with the lowest common multiples.
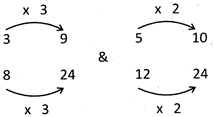
It is now easy to see that \[\frac{9}{24}\] is smaller than\[\frac{10}{24}\] (because 9 is smaller than 10 so, \[\frac{5}{12}>\frac{3}{8}.\]
![]()
Which one is greater: \[\frac{5}{6}\,or\,\frac{13}{15}\]
Solution:
The least common multiple of 6 and 15 is 30. So let's do some multiplication to make each denominator equal to 30:
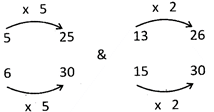
Now we can easily see that \[\frac{26}{30}\] is greater than \[\frac{25}{30}\]so, \[\frac{13}{15}>\frac{5}{6}\]
This method is useful in arranging the fractions (more than two) either in ascending or descending order.
Short Cut Method for comparing two Fractions
Suppose you have to compare two fractions \[\frac{A}{B},\frac{C}{D}\] then you simply multiply numerator of the first fraction with the denominator of the second \[\left( i.e\times AD \right)\] and vice versa \[\left( i.e\text{ }B\times C \right)\].Compare the product \[A\times D\]and\[B\times C,\]
![]()
Compare \[\frac{241}{2123}\]and \[\frac{293}{2189}\]
Solution:
Here, numerator and denominator of first and second fraction are (241, 2123) and (293, 2189) respectively.
We have to find the products as above mentioned method, i.e \[241\times 2189\] and 293 x 2123.
Here, \[241\times 2189=527549\]and \[293\times 2123=622039\]
Since 527549 < 622039 m, therefore, \[\frac{241}{2123}<\frac{293}{2189}\]
![]() Additions of the Fractions
Additions of the Fractions
Addition of the Fractions with Equal Denominator.
Step 1: Make sure the denominators are the same.
Step 2: Add the numerators. Put the answer over the same denominator.
Step 3: Reduce the fraction into simplest form
![]()
Add \[\frac{123}{2124},\frac{167}{2124},\frac{253}{2124},\frac{189}{2124},\frac{79}{2124}\]and \[\frac{131}{2124}\]
Solution:
\[\frac{131}{2124}+\frac{167}{2124}+\frac{253}{2124}+\frac{189}{2124}+\frac{79}{2124}+\frac{131}{2124}\]
Here denominators are same. Therefore, we add numerators as follows:
\[=\frac{123+167+253+189+79+131}{2124}=\frac{942}{2124}\]
After reducing it into simplest form, we get \[=\frac{157}{354}\]
\[\frac{123}{2124}+\frac{167}{2124}+\frac{253}{2124}+\frac{189}{2124}+\frac{79}{2124}=\frac{157}{354}\]
Addition of the Fractions with Unequal Denominator
Step 1: Make sure the denominators are unequal
Step 2: Make denominators equal by taking LCM
Step 3: Add the numerators. Put the answer over the same denominator.
Step 4: Simplify the fraction (if needed).
![]()
Simplify \[\frac{23}{24}+\frac{16}{21}+3\frac{5}{8}+7\frac{9}{14}+5\frac{8}{15}\]
Solution:
\[\frac{23}{24}+\frac{16}{21}+3\frac{5}{8}+7\frac{9}{14}+5\frac{8}{15}\]
\[\frac{23}{24}+\frac{16}{21}+\frac{29}{8}+\frac{107}{14}+\frac{83}{15}\]
Here denominators are different, then we take the LCM of denominators to make equal. LCM of 24, 21, 8, 14, 15 = 840.
Therefore, \[\frac{23\times 35}{24\times 35}=\frac{805}{840},\frac{16\times 40}{21\times 40}=\frac{640}{840},\frac{29\times 105}{8\times 105}\] \[=\frac{3045}{840},\frac{107\times 60}{14\times 60}=\frac{6420}{840},\frac{83\times 56}{15\times 56}=\frac{6448}{840}.\]
Now \[\frac{23}{24}+\frac{16}{21}+\frac{29}{8}+\frac{107}{14}+\frac{83}{15}\]
\[=\frac{805}{840}+\frac{640}{840}+\frac{3045}{840}+\frac{6420}{840}+\frac{4648}{840}\]\[=\frac{15558}{840}=\frac{2593}{140}=18\frac{73}{140}\]
![]() Subtraction of the Fractions
Subtraction of the Fractions
Steps to Subtract Fractions
Step 1: Make sure the denominators are the same
Step 2: Subtract the numerators. Put the answer over the same denominator.
Step 3: Simplify the fraction.
![]()
Simplify: \[\frac{813}{940}-\frac{189}{940}\]
Solution:
Step 1: The denominator are already the same.
Step 2: Subtract the numerator and put the answer over the same denominator.\[=\frac{813-189}{940}=\frac{624}{940}\]
Step 3: Simplify the fraction: \[\frac{624}{940}=\frac{156}{235}\]
![]() Multiplication of the Fractions
Multiplication of the Fractions
Multiplication of fractions that contain polynomials is similar to multiplication of fractions that contain only arithmetic numbers. If this fact is kept in mind the student will have little difficulty in mastering multiplication in algebra. For instance: we recall that to multiply a fraction by a whole number, it is simply the multiplication of the numerator by the whole numbers. This is illustrated in the following example:
Multiplication of fractions that contain numbers, (Arithmetic), \[4\times \frac{3}{17}=\frac{12}{17}\]
Multiplication of fractions that contain polynomials, (Algebra), \[(x-4)\frac{3}{{{x}^{2}}-5}=\frac{3x-12}{{{x}^{2}}-5}\]
Working Rule for Multiplication of Fractions
Step 1: Find the product of numerators
Step 2: Find the product of denominators Product of numerators
Step 3: Write the product of fractions as \[\frac{product\,of\,numerators}{product\,of\,deno\min ators}\]and simplify it.
\[\frac{a}{b}\times \frac{c}{d}\times \frac{e}{f}\times \frac{g}{h}=\frac{a\times c\times e\times g}{b\times d\times f\times h}=\frac{Product\text{ }of\text{ }numerators}{Product\text{ }of\text{ }denominators\,}\]
![]()
Simplify the arithmetic expression\[\frac{12}{23}\times 6\frac{4}{7}\times 4\frac{1}{5}\times 5\frac{7}{18}\]
Solution:
Given expression is \[=\frac{12\times 46\times 21\times 97}{23\times 7\times 5\times 18}=\frac{388}{5}=77\frac{3}{5}\]
Reciprocal of Fraction
Two fraction are said to be reciprocal to each other if their product is 1.
![]()
\[\frac{b}{a}\]is the reciprocal of \[\frac{a}{b}\] because \[\frac{a}{b}\times \frac{b}{a}=1\]
![]() Division of the Fraction
Division of the Fraction
Step 1: Find the reciprocal of divisor.
Step 2: Multiply dividend with divisor as rule of multiplication.
Step 3: Simplify it if possible.
![]()
\[\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\times \frac{d}{c}=\frac{a\times d}{b\times c}\left( because\frac{d}{c}is\,the\,reciprocal\,of\,\frac{c}{d} \right)\]
Reducing Algebraic Fractions to Lowest Term
There are many useful applications of factorizing. One of the most important application is that of simplifying algebraic fractions that contain algebraic expressions as the numerator denominator or both can be reduced to lowest term. If the terms of a fraction are monomials then common factors are immediately apparent as in the following expression
\[\frac{3{{x}^{2}}y}{6xy}=\frac{3xy(x)}{3xy(2)}=\frac{x}{2}\]
If the numerator and denominator of an algebraic fraction are polynomial then find the linear factors of. Polynomial and reduce the common factors.
As in the following example:
Simplification of Algebraic Expression
Find the factor of numerator and denominator separately. Observe the factor and if there is any common term, cancel it (keep in mind cancel the terms of numerator with denominator only).
Simplify the algebraic expression \[\frac{a+b}{a-}\times \frac{a}{a-b}.\]
Step1: Multiply the numerators of the fractions, \[\left( a\text{ }+\text{ }b \right)\times a=a\left( a+b \right)={{a}^{2}}+ab\]
Step2: Multiply the denominators of the fractions, \[\left( a-b \right)\times \left( a-b \right)={{a}^{2}}-ab-ab+{{b}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\]
Step 3 : Simplification is not required,
Therefore, \[\frac{a+b}{a-b}\times \frac{a}{a-b}=\frac{a\left( a+b \right)}{{{\left( a-b \right)}^{2}}}=\frac{{{a}^{2}}+ab}{{{a}^{2}}-2ab+{{b}^{2}}}\]

![]() A boy was asked to multiply a given number by \[\left( \frac{8}{17} \right).\] Instead he divided the given number by \[\left( \frac{8}{17} \right)\]and got the result 225 more than that number, The given number was____.
A boy was asked to multiply a given number by \[\left( \frac{8}{17} \right).\] Instead he divided the given number by \[\left( \frac{8}{17} \right)\]and got the result 225 more than that number, The given number was____.
(a) 8
(b) 17
(c) 64
(d) 136
(e) None of these
Answer: (d)
Explanation
Suppose the given number be x,
According to question, \[x\left( \frac{17}{8} \right)-x\left( \frac{8}{17} \right)=255,\,or\,\frac{225}{136}x=\left( 225\frac{136}{225} \right)=136.\]
![]() In an examination, a student was asked to find \[\left( \frac{3}{14} \right)\] of a certain number. By mistake he found \[\left( \frac{3}{4} \right)\] of that number. His answer was 150 more than the correct answer. Find the number.
In an examination, a student was asked to find \[\left( \frac{3}{14} \right)\] of a certain number. By mistake he found \[\left( \frac{3}{4} \right)\] of that number. His answer was 150 more than the correct answer. Find the number.
(a) 180
(b) 240
(c) 280
(d) 290
(e) None of these
Answer: (c)
Explanation
Let the number be y, according to question. \[\left( \frac{3}{4} \right)y-\left( \frac{3}{14} \right)y=150\] or \[\frac{15}{28}y=150,\therefore y=150\left( \frac{28}{15} \right)=280\]
![]() If we multiply a fraction by itself and divide the product by its reciprocal then we get the fraction \[18\frac{26}{27}\] Which one of the following fractions is the original fraction?
If we multiply a fraction by itself and divide the product by its reciprocal then we get the fraction \[18\frac{26}{27}\] Which one of the following fractions is the original fraction?
(a)\[1\frac{8}{29}\]
(b) \[2\frac{2}{3}\]
(c) \[1\frac{1}{3}\]
(d) \[1\frac{9}{5}\]
(e) None of these
Answer: (b)
![]() In a college,\[\frac{1}{5}\] the of the girls & \[\frac{1}{8}\]the of the boys participate in a social camp. What is the total number of students in the college participates in the camp?
In a college,\[\frac{1}{5}\] the of the girls & \[\frac{1}{8}\]the of the boys participate in a social camp. What is the total number of students in the college participates in the camp?
(a) \[\frac{13}{40}\]
(b) \[\frac{13}{80}\]
(c) \[\frac{2}{13}\]
(d) \[\frac{1}{8}\]
(e) None of these
Answer: (a)
![]() Jasmine spends \[\frac{\mathbf{3}}{\mathbf{5}}\mathbf{th}\] of her income on household articles and \[\frac{\mathbf{1}}{\mathbf{7}}\mathbf{th}\]of her income is her personal expanses. If her monthly income is $ 7000 then her monthly saving is ________
Jasmine spends \[\frac{\mathbf{3}}{\mathbf{5}}\mathbf{th}\] of her income on household articles and \[\frac{\mathbf{1}}{\mathbf{7}}\mathbf{th}\]of her income is her personal expanses. If her monthly income is $ 7000 then her monthly saving is ________
(a) $ 9000
(b) $ 18000
(c) $ 12000
(d) $ 7000
(e) None of these
Answers: (b)
You need to login to perform this action.
You will be redirected in
3 sec
