7th Class Mathematics Decimals and Fractions Fractions and Decimals

FRACTIONS AND DECIMALS

 

FUNDAMENTALS

• A fraction is a part of a whole.
• A number of the form\[\frac{p}{q}\], where p and q are whole numbers and \[q\ne 0\]is known as a fraction.
• In the fraction\[\frac{p}{q}\], p is called the numerator and q is called the denominator.

 

Various Types of Fractions

1. Improper fraction: A fraction whose numerator is greater than or equal to its denominator is called an improper fraction. If number is written as\[\frac{N}{D}\], then \[N~\underline{>}\,D\]where N = numerator D = Denominator e.g.,\[\frac{100}{100},\] \[\frac{51}{50},\] \[\frac{45}{2},.....\]etc.
2. Proper fraction: A fraction whose numerator is less than its denominator is called a proper fraction. e.g.,\[\frac{3}{8},\,\,\frac{6}{7},\,\,\frac{9}{16},\,\,\frac{8}{18},......\]etc.
3. Decimal fraction: A fraction whose denominator is 10, 100, 1000 etc., is called a decimal fraction. e.g., \[\frac{2}{10},\,\,\frac{8}{100},\,\,\frac{26}{1000},\,\,\frac{1312}{1000},......\]etc.
4. Vulgar fraction: A fraction whose denominator is a whole number other than 10, 100, 1000, etc., is called a vulgar fraction. e.g., \[\frac{3}{8},\,\,\frac{6}{7},\,\,\frac{9}{16},\,\,\frac{83}{103},\,\,......\]etc.
5. Simple fraction: A fraction in its lowest terms is known as a simple fraction. e.g., \[\frac{3}{8},\,\,\frac{6}{7},\,\,\frac{9}{16},\,\,\frac{8}{17},\,\,......\]etc.
6. Mixed fraction: A number which can be expressed as the sum of a natural number and a proper fraction is called a mixed fraction.

e.g., \[5\frac{2}{3},\,\,6\frac{1}{6},\,\,1\frac{3}{4},\,\,107\frac{1}{2},\,\,.......\]etc.           

\[5\frac{2}{3}\]can be written as \[5+\frac{2}{3}\]

7. Like fractions: Fractions having the same denominator but different numerators are called like fractions. e.g.\[\frac{6}{17},\,\,\frac{9}{17},\,\,\frac{11}{17},\,\,......\]etc.
8. Unlike fractions: Fractions having different denominators are called unlike fractions. e.,\[\frac{3}{4},\,\,\frac{6}{7},\,\,\frac{5}{6},\,\,\frac{4}{5},\,\,\frac{8}{13},\,\,.......\]etc.

• An important property: If the numerator and denominator of a fraction are both multiplied by the same non zero number, its value is not changed. Thus, \[\frac{2}{7}=\frac{2\times 2}{7\times 2}=\frac{2\times 5}{7\times 5}......\]etc.
• Equivalent fractions: A given fraction and the fraction obtained by multiplying (or dividing) its numerator and denominator by the same non — zero number, are called equivalent fractions. (See above property) e.g., Equivalent fractions of \[\frac{6}{12}\]are \[\frac{8}{16},\frac{1}{2},\frac{4}{8},\frac{5}{10}\]......etc.

 

• Method of changing unlike fraction to like fraction:

Step - 1: Find the L.C.M. of the denominators of all the given fractions.

Step - 2: Change each of the given fractions into an equivalent fraction having denominator equal to the L.C.M. of the denominators of the given fraction.

e.g., Convert the fractions \[\frac{1}{6},\,\,\frac{4}{9}\] and \[\frac{70}{12}\] into like fractions.

L.C.M. of 6, 9 and \[12=3\times 2\times 3\times 2=36\]

Now, \[\frac{1}{6}=\frac{1\times 6}{6\times 6}=\frac{6}{36};\frac{4}{9}=\frac{4\times 4}{9\times 4}=\frac{16}{36}\] and\[\frac{70}{12}=\frac{70\times 3}{12\times 3}=\frac{21}{36}\].

Clearly, \[\frac{6}{36},\frac{16}{36}\] and \[\frac{21}{36}\] are like fractions.

Utility: This method is used for comparing fractions

• Irreducible fractions : A fraction \[\frac{a}{b}\] is said to be irreducible or in lowest terms,

If the H.C.F. of a and b is 1. They are also called simple fractions.

If H.C.F. of a and b is not 1, then \[\frac{a}{b}\] is said to be reducible.

• Comparing fraction: Let \[\frac{a}{b}\] and \[\frac{c}{d}\] be two given fractions. Then,

(a) \[\frac{a}{b}\text{}\frac{c}{d}\text{ }\Leftrightarrow ad>bc~~\]                     (b) \[\frac{a}{b}\text{=}\frac{c}{d}\text{ }\Leftrightarrow ad=bc~~\]                       (c) \[\frac{a}{b}\text{}\frac{c}{d}\Leftrightarrow \text{ }ad<bc\]

These are important results and should be committed to memory. (or understood as coming out of cross = multiplication).  

• Method of comparing more than two fractions;

Step - 1: Convert all the given fractions into like fractions, each having same denominator (follow the method as given above).

Step - 2: Now, if we compare any two of these like fractions, then the one having larger numerator, is larger.

• Addition and subtraction of fractions:

(a) Add / Subtract like fractions:

e.g., (1)  Add \[\frac{2}{9}\]and \[\frac{4}{9}\]

\[\frac{2}{9}+\frac{4}{9}=\frac{2+4}{9}=\frac{6}{9}\]

e.g., (2) Subtract \[\frac{4}{7}\] from\[\frac{6}{7}\].

\[\frac{6}{7}-\frac{4}{7}=\frac{6-4}{7}=\frac{2}{7}\]

 

(b) Add/Subtract unlike fractions:

To add/subtract unlike fractions, first convert them into like fractions and proceed as above.

e.g., (1) Add \[\frac{1}{3},\frac{3}{5}\]and\[\frac{4}{7}\].

L.C.M of 3, 5 and 7 is 105.

\[\therefore \,\,\frac{1}{3}+\frac{3}{5}+\frac{4}{7}=\frac{35}{105}+\frac{63}{105}+\frac{60}{105}=\frac{35+63+60}{105}=\frac{158}{105}=1\frac{53}{105}\]

e.g., (2) Subtract\[\frac{1}{4}\]from\[\frac{11}{12}\].

\[\frac{11}{12}-\frac{1}{4}=\frac{11-3}{12}=\frac{8}{12}=\frac{2}{3}\]

 

• Multiplication of fraction, by a whole number:

(a) Proper / Improper fraction: In order to multiply a whole number with a proper or an improper fraction, we multiply the whole number with the numerator of the fraction, keeping the denominator same.

e.g., \[6\times \frac{16}{17}=\frac{96}{17}=5\frac{11}{17}\]

(b) Multiplying a whole number by a mixed fraction: In order multiply a whole number by a mixed fraction, first covert the mixed fraction to an improper fraction and then multiply.

e.g.,\[21\times 6\frac{3}{7}=21\times \frac{45}{7}=145\]

(c) Multiplying a fraction by a fraction: In order to multiply a fraction by another fraction, we take the product of their numerators and divide it by the product of their denominators. The result is then expressed in lowest terms i.e., if \[\frac{a}{b}\] and \[\frac{c}{d}\] are the fractions, then their product is \[\frac{ac}{bd}\] (expressed in the lowest terms).

Elementary question

Express in lowest terms the following number \[\frac{10}{23}\times \frac{46}{47}\]

Ans.     \[\frac{10\times 46}{23\times 47}=\frac{460}{1081}\]; this is expressed m lowest terms as\[\frac{20}{47}\].

 

• Reciprocal of a fraction:

Two fractions are said to be the reciprocal of each other, if their product is 1.

e.g., \[\frac{3}{7}\] and \[\frac{7}{3}\] are the reciprocals of each other, since\[\left( \frac{3}{7}\times \frac{7}{3} \right)=1.\]

In general, if \[\frac{a}{b}\]is a non-zero fraction, then its reciprocal is \[\frac{b}{a}\].

Example: Reciprocal of \[{}^{6}/{}_{7}\] is \[\frac{1}{{}^{6}/{}_{7}}=1\times \frac{7}{6}=\frac{7}{6}\]

Note: Reciprocal of 0 does not exist.

• Division of fractions:

(a) Division of a whole number by any fraction: In order to divide a whole number by a fraction, we have to multiply the whole number by the reciprocal of the given fraction.

e.g., \[3\div 2\frac{2}{5}=3\div \frac{12}{5}=\frac{3\times 5}{12}=\frac{5}{4}\]

(b) Division of a fraction by a whole number: In order to divide a fraction by a whole number, we have to multiply the given fraction by the reciprocal of the whole number.

e.g., \[4\frac{2}{5}\div 11=\frac{22}{5}\times \frac{1}{11}=\frac{2}{5}\]

While dividing a mixed fraction by a whole number, convert the mixed fraction into an improper fraction and then divide.

(c) Division of a fraction by another fraction: In order to divide a fraction by another fraction, we have to multiply the first fraction by the reciprocal of the second.

1. g., \[3\frac{1}{4}\div 2\frac{1}{5}=\frac{13}{4}\div \frac{11}{5}=\frac{13}{4}\times \frac{5}{11}=\frac{65}{44}=1\frac{21}{44}\]

Decimals

• The number expressed in decimal form are called decimal numbers or simply decimals.

e.g., 6.0, 16.53, 26.67, 0.012 etc.

• A decimal number has two parts, namely

(i) Whole - number part and                     (ii) Decimal part

These parts are separated by a dot (.), called the decimal point.

 

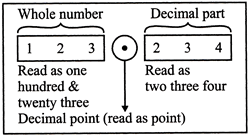
Hence, read as one hundred twenty three point two three four

• Representing decimals on number line: Let us represent 0.6 on the number line.

0.6 lies between 0 and 1.

0.6 is 6 tenths.                                                                           

So, divide the unit length between 0 and 1 into 10 equal parts & take 6 parts as shown.

 

• The number of digits in the decimal part of a decimal number given the number of decimal places.

e.g., 6.29 has two decimal places and 7.123 has three decimal places.

• Decimals having the same number of decimal places are called like decimals,

e.g., 6.66, 7.03, 18.21 etc.,

• Decimal having different number of decimal places are called unlike decimals,

e.g., 333.1, 226.02, 111.111 etc.,

 

Note: Adding any number of zeros to the extreme right of the decimal part of a decimal number does not change its value.

e.g., 3.13 = 3.130 = 3.1300 etc.

Comparing decimals.

Step - 1: Convert the given decimal numbers into like decimals.

Step - 2: First compare the whole - number part.

Step - 3: 'If the whole number parts are equal, compare the tenths digit. The decimal number with the greater digit in the tenths place is greater.

Step - 4: If the tenths digits are also equal, compare the hundredths digits, and so on.

e.g.,      (i) 66.27 > 63.27

(ii) 21.65 > 21.45

(iii) 202.013 < 202.018

 

• Conversion of decimals to fractions:

e.g., express 6.16 as a fraction.

Step - 1:  In the numerator, write the give decimal number without the decimal point.

\[6.16=\frac{616}{\left( \,\,\,\,\, \right)}\]

Step - 2:   From 'right to left', count the number of decimal places, say 'x'. Here x = 2.

Step - 3:  hi the denominator, write 1 followed by 'x' number of zeros. \[6.16=\frac{616}{100}\]

Step - 4: Simplify the obtained fraction into its lowest terms. \[\frac{616}{100}=\frac{154}{25}\]

• Conversion of fractions to decimals:

(i) Conversion of decimal fraction to decimal.

Express \[\frac{27153}{1000}\] as a decimal

Step - 1: Write the numerator as it is, 27153.

Step - 2: Count the number of zeros in the denominator. Let it be 'x'. Here x = 3.

Step - 3: From 'right to left' in the number, place the decimal point after 'x' places.

\[\therefore \,\,\,\frac{27153}{1000}=27.153\]

(ii) Conversion of a non-decimal fraction into a decimal.

Express \[\frac{618}{7}\] as a decimal.

Step - 1: Divide the number as usual.

Step - 2: If dividend is less than divisor, place the decimal point in quotient.

Step - 3: Place a zero m the dividend.

Step - 4: Repeat the division process till remainder is zero or as per the required number of decimal places.

Note:-   (a) Express \[\frac{618}{7}\] as a decimal (upto 3 decimal) \[\frac{618}{7}=88.285\]

(b) Express \[\frac{618}{7}\] as a decimal (upto 2 decimals) \[\frac{618}{7}=88.28\]