7th Class Mathematics Integers

Integers

• Natural numbers (N): Counting numbers 1, 2, 3,…... etc., are called natural numbers.

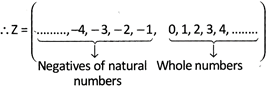
            N= {1, 2.3, 4, …….}

• Representation of natural numbers on a number line: To represent natural numbers on a number line we should draw a line and write the numbers at equal distances on it as shown.

• Whole Numbers (W): The set of natural numbers together with zero is known as the set of whole numbers.

            W= {0, 1, 2, 3 …...}

• Integers (Z): The set containing negatives of natural numbers along with whole numbers is called the set of integers.

1, 2, 3, 4, .... etc., are called positive integers and are denoted by\[{{Z}^{+}}\].

            \[\therefore \]\[{{Z}^{+}}\]= {1, 2, 3, 4, .......}

            -1, - 2, -3, - 4,  ...... etc., are called negative integers and are denoted by\[{{Z}^{-}}\].

            \[\therefore \]\[{{Z}^{-}}\]= {..............-3,-2,-1}

            Note:    1.Usually negative numbers are placed in brackets to avoid confusion arising due to two signs I evaluations. e.g., 3+ (-5) =-2

2. 0 is not included in ether\[{{\mathbf{Z}}^{\mathbf{+}}}\,\mathbf{or}\,{{\mathbf{Z}}^{\mathbf{-}}}\]. Hence, it is non – negative.

            (i) To represent quantities like profit, income, increase, rise, high, north, east, above, depositing, climbing and so on, positive numbers are used.

            (ii) To represent quantities like loss, expenditure, decrease, fall, low, south, west, below, withdrawing, sliding and so on, negative numbers are used.

            Note:    1. 0 is neither positive nor negative.

2. The + sign is not written before a positive number.

            3.\[\frac{1}{2}\] and 0.3 are not integers as they are not whole numbers.

• Representation of integers on a number line: Integers are represented on the number line as shown.

On a number line when we

            (a) Add a positive integer, we move to the right.

            (b) Add a negative integer, we move to the left.

            (c) Subtract a positive integer, we move to the left.

            (d) Subtract a negative integer, we move to the right.

• Properties of integers:

            (i) Closure property: Closure property is satisfied with respect to addition, subtraction and multiplication in the set of integers.

            For a, b e Z, a + b e Z, a - b \[\in \] Z and a b\[\in \] Z.

            (ii) Commutative property: Commutative property is satisfied with respect to addition and multiplication in the set of integers.

            If a, b \[\in \]Z, then a + b = b + a and a \[\times \] b = b \[\times \] a.

            If a, b, c \[\in \] Z, then

            a + (b + c) = (a + b) + c = c + (b + a) and a \[\times \] (b \[\times \] c) = (a \[\times \] b) \[\times \] c = c \[\times \] (b \[\times \] a).

• Distributive property: Multiplication is distributed over addition and subtraction in the set of integers.

            For a, b and c e Z, a (b + c) = ab + ac and a (b - c) = ab - ac.

• Identity element: 0 is the identity under addition and 1 is the identity under multiplication.

            For a e Z, a+0=a=0+a and a\[\times \]1 = a = 1 \[\times \] a.

• Multiplication by zero: For any integer a, a 0=0 a=0.