Properties of Integers
Category : 7th Class
There are four properties of Integers
![]() Properties of Addition
Properties of Addition
Closure Property
The sum of two integers is always an integer.
For any two integer's p and q, \[\Rightarrow p+q\] is an integer.
For example \[\left( -\text{ }4 \right)+3=\left( -\text{ }1 \right),\] Which is an integer.
Commutativity
Sum of two integers is commutative.
For any two integers p and q,\[~\Rightarrow p+q=q+p,\] for example \[7+\left( -6 \right)=1\]and \[\left( -\text{ }6 \right)+7=1,\] therefore \[7\text{ }+\text{ }\left( -\text{ }6 \right)\text{ }=\text{ }\left( -6 \right)+7\]
Associativity
We addition of integers is associative. For any three integers p, q and r, \[p+\left( q+r \right)=\left( p+q \right)+r,\]
![]()
\[\left( -4 \right)+\left\{ \left( -8 \right)+6 \right\}=\left\{ \left( -4 \right)+\left( -8 \right) \right\}+6\]
Solution:
L.H.S \[=\left( -4 \right)+\left\{ \left( -\text{ }8 \right)+6 \right\}R.H.S=\left\{ \left( -4 \right)+\left( -8 \right) \right\}+6\]
\[=(-4)+(-2)=(-12)+6=(-6)=(-6)\]
Additive Identity
Additive identity is the number which when added to an integer gives the same integer. In case of addition "0" is the identity for integers. For example:
(i) \[~\left( -8 \right)+0=\left( -8 \right)\]
(ii) \[~0+\left( -37 \right)=\left( -37 \right)\]
(iii) \[31+0=37\]
Additive Inverse
The additive inverse of an integer is that integer which when added to the given integer gives the additive identity \[0.\left( -p \right)\] is the additive inverse of p, i.e. \[p+\left( -p \right)\] = 0. We get the additive inverse by taking the negative of the given integer. For example ( - 10) is additive inverse of 10 and 20 is the additive inverse of (-20)
![]() Properties of Subtraction
Properties of Subtraction
Closure Property
Integers are closed under subtraction. If a and b are two integers then a - b is also an integer.
For example
(i) \[7-9=-2\] is an integer
(ii) \[\left( -8 \right)-\left( -15 \right)=7\] is an integer
Subtraction is neither Commutative nor Associative
For any two numbers a and \[b,a-b\ne b-a\] and for any three integers a, b, c we have \[a-(b-c)\ne (a-b)-c\]
(i) \[9-3\ne 3-9\]
(ii) \[9-(3-2)\ne (9-3)-2\]

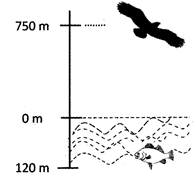
![]() A bird is flying at the height of 750 m above the lake surface. At a particular point it is exactly above a fish swimming 120 m below the lake surface. What is the vertical separation between bird and fish?
A bird is flying at the height of 750 m above the lake surface. At a particular point it is exactly above a fish swimming 120 m below the lake surface. What is the vertical separation between bird and fish?
(a) 150m
(b) 350m
(c) 870m
(d) 630m
(e) Data is insufficient
Answer: (c)
Explanation
Distance between bird and fish | 750 m|+|-120 m| = 750 m+120 m = 870 m
Therefore, option (C) is correct and rest of the options is incorrect.
![]() In London temperature was \[-\text{ }9{}^\circ c\]on Monday and then dropped by \[2{}^\circ c\] on next day. On Wednesday it raised by again. The temperature on Wednesday was:
In London temperature was \[-\text{ }9{}^\circ c\]on Monday and then dropped by \[2{}^\circ c\] on next day. On Wednesday it raised by again. The temperature on Wednesday was:
(a)\[7{}^\circ c\]
(b) \[-4{}^\circ c\]
(c)\[-11{}^\circ c\]
(d) 18°c
(e) None of these
Answer: (b)
![]() John goes 17 km towards north from a point P to another point Q. From Q he moves 27 km towards south along the same road. If the distance towards north is represented by positive integer then which integer will represent his final distance from P?
John goes 17 km towards north from a point P to another point Q. From Q he moves 27 km towards south along the same road. If the distance towards north is represented by positive integer then which integer will represent his final distance from P?
(a) \[-10km\]
(b) 44km
(c)\[~-34km~\]
(d) 10km
(e) None of these
Answer: (a)
![]() There are 40 questions in the test booklet of Mathematics Olympiad. If Stephen scores 80 marks when 5 marks are awarded for each correct answer and 3 marks is deducted for each incorrect answer then find the number of correct answer attempted by Stephen.
There are 40 questions in the test booklet of Mathematics Olympiad. If Stephen scores 80 marks when 5 marks are awarded for each correct answer and 3 marks is deducted for each incorrect answer then find the number of correct answer attempted by Stephen.
(a) 16
(b) 20
(c) 28
(d) 25
(e) None of these
Answer: (d)
![]() If X and Y are two positive integers so that X > Y and P, Q are the additive inverse of X and Y respectively, then which of the following is correct?
If X and Y are two positive integers so that X > Y and P, Q are the additive inverse of X and Y respectively, then which of the following is correct?
(a)\[~X+Y+P-Q=Y~\]
(b)\[~\left( X+Y \right)-\left( P+Q \right)=0\]
(c)\[2\left( X+Y \right)+\left( P+Q \right)=-\left( P+Q \right)\]
(d) \[\left( X+Y \right)+\left( P+Q \right)=2\left( P+Q \right)\]
(e) None of these
Answer: (c)
![]() Properties of Multiplication
Properties of Multiplication
Closure Property
For any two integers 'm' and 'n', the product ?m' and 'n' is always an integer.
For example:
(i) \[8\times 3=24\text{ },\]which is an integer.
(ii) \[~7\times \left( -5 \right)=-35,\]which is an integer.
Commutativity
Multiplication of integers is commutative.
For any two integers m and n, \[m\times n=n\times m\]
For example: \[8x\left( -\text{ }7 \right)=-\left( 8\text{ }x\text{ }7 \right)=-56\] and \[\left( -\text{ }7 \right)\times 8=-\left( 7\text{ }\times \text{ }8 \right)=-56\]
Associativity
The multiplication of integers is associative.
For any three integers m, n and \[p,\times m\times \left( n\times p \right)=\left( m\times n \right)\times \text{ }p,\]for example \[\left( -12 \right)\times \left\{ 5\text{ }x\left( -2 \right) \right\}=\left( -12 \right)\times \left( -10 \right)=120\] and \[\left\{ \left( -12 \right)\times 5 \right\}\times \left( -2 \right)=\left( -60 \right)\times \left( -2 \right)=120.\] \[\therefore \left( -\text{ }12 \right)\times \left\{ 5\times \left( -2 \right) \right\}=\left\{ \left( -12 \right)\times 5 \right\}\times \left( -2 \right)\]
Multiplicative Identity
The multiplicative identity of a number is that number which when multiplied with the given integer results the same integers. "1" is the multiplicative identity for any integers. For any integers 'm' we can write \[1\times m=m=m\times 1\]
Multiplicative Inverse
An inverse element usually does not exist at all. For example "0" is an integer whose inverse does not exist.
Distributive Property of Multiplication on Addition
For any three integers m, n, p, we have:
(i) \[m\times \left( n+p \right)=\left( m\times n \right)+\left( m\times p \right)\]
(ii) \[\left( n+p \right)\times m=n\times m+n\times p\]
![]() Properties of Division
Properties of Division
For any two integer p and q
(i) \[p<q\Rightarrow p\div r<q\div r,\]if r is positive.
(ii) \[p<q\Rightarrow p\div r>q\div r,\]if r is negative.
![]()
What feast value must be given to '*' so that the number 97215*6 is divisible by 11 ?
(a) 11
(b) 12
(c) 3
(d) 15
(e) None of these
Answer: (c)
Explanation
\[\left( 9+2+5+6 \right)-\left( 7+1+x \right)=14-x,\]must be divisible by 11. So, \[x=3.\]
![]()
What least value must be given to '*' so that the number 91876*2 is divisible by 8?
(A) 1
(b) 2
(c) 3
(d) 4
(e) None of these
Answer: (C)
Explanation
By hit and trial, we find that 9187632 is divisible by 8. So '*' must be replaced by 3.
![]()
Which one of the following numbers is exactly divisible by 99?
(a) 3572404
(b) 135792
(c) 913464
(d) 114345
(e) None of these
Answer: (d)
Explanation
We know that if a number is divisible by 9 and 11 both then that number must be divisible by 99. Clearly 114345 is divisible by 9 and 11. So, it is divisible by 99.
![]()
\[\frac{392}{\sqrt{?}}=28\]
(a) 144
(b) 196
(c) 24
(d) 48
(e) None of these
Answer: (b)
Explanation
let, \[\frac{392}{\sqrt{x}}=28\]
Therefore, \[28\sqrt{x}=392\]{By cross multiplication}
\[\sqrt{x}=\frac{392}{28}\Rightarrow x={{(14)}^{2}}=196\]

![]() The largest number of four digits exactly divisible by 88 is:
The largest number of four digits exactly divisible by 88 is:
(a) 9768
(b) 8888
(c) 9988
(d) 9944
(e) None of these
Answer: (d)
Explanation
Largest number of four digits = 9999.
Required number \[=\text{ }9999\text{ }-\] {Remainder of \[\left( 9999\div 88 \right)\}\]
\[\therefore \]Required number \[=9999-55=9944\]
![]() The least number of five digit exactly divisible by 456 is?
The least number of five digit exactly divisible by 456 is?
(a) 10142
(b) 10232
(c) 10032
(d) 10012
(e) None of these
Answer: (C)
Explanation
Least number of five digits = 10000
Required number \[=10000+(456-\]remainder of division, 10000 by 456) \[=\text{ }10000\text{ }+\text{ }\left( 456-424 \right)=10000+32=10032.\]
![]() What least number must be subtracted from 13601 to get a number exactly divisible by 87?
What least number must be subtracted from 13601 to get a number exactly divisible by 87?
(a) 49
(b) 23
(c) 29
(d) 31
(e) None of these
Answer: (c)
![]() What least number must be added to 1056 to get a number exactly divisible by 23?
What least number must be added to 1056 to get a number exactly divisible by 23?
(a) 21
(b) 25
(c) 13
(d) 2
(e) None of these
Answer: (d)
![]() What least value must be given to '*' so that the number 6135*2 is exactly divisible by 9?
What least value must be given to '*' so that the number 6135*2 is exactly divisible by 9?
(a) 0
(b) 1
(c) 12
(d) 13
(e) None of these
Answer: (b)
You need to login to perform this action.
You will be redirected in
3 sec
