9th Class Mathematics Quadrilaterals Important Points

       Important Points

(i) A quadrilateral is a parallelogram if their opposite sides are equal.

(ii) A quadrilateral is a parallelogram if their opposite angles are equal.

(iii) If the diagonal of a quadrilateral bisect each other then it is a parallelogram.

(iv) A quadrilateral is a parallelogram if its one pair of opposite sides are equal and parallel.

(v) The diagonals of rectangle are equal.

(vi) If the two diagonals of a parallelogram is equal then the parallelogram is a rectangle.

(vii) The diagonal of the rhombus are perpendicular bisector of each other.

(viii) A parallelogram is a square if the diagonals of a parallelogram are equal and bisector at right angle.  

            Intercept Theorem

If a transversal intersect three and more than three parallel lines in such a way that all the intercepts are equal then the intercept on any other transversal is also equal.  

Given:

Three parallel lines a, b, c intersected by a transversal \[x\] at L, M, N respectively so that LM = MN. Another transversal y cutting a, b, c at T, U, V respectively

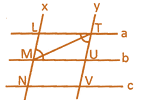
Proof:

Since \[\text{LT  }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{  MU}\] and \[~\text{LM  }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{  TU}\]

\[\therefore \] LMUT is a parallelogram \[\therefore \] TU = LM                                                     .....(i)

Similarly                

MNVU is a parallelogram

\[\therefore \] MN=UV                                                    .....(ii)

But \[\therefore \] TU = UV

Now In

\[\Delta \text{MLT}\]and \[\Delta \text{TUM}\]          (Alternate)

\[\angle \text{MTL}=\angle \text{MTU}\]                                (Opposite angle of Parallelogram)

LT = UM                                        (Opposite sides of Parallelogram)                

MT=MT                                (Common)                

\[\therefore \] By SOS                

\[\Delta \text{MTL}\cong \Delta \text{TUM}\]                

By CPCT,                

LM=TU                                             

Similarly                

MN=UV But                

LM=MN                

\[\therefore \] TU = UV