9th Class Mathematics Quadrilaterals Results on Area of Quadrilateral

       Results on Area of Quadrilateral

(i) Any diagonal of a parallelogram divides it into two triangles of equal area.

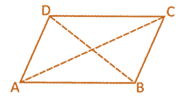
In the above given figure,

\[\text{ar(}\Delta \text{ABC})=\text{ar}(\Delta \text{ACD)}\]

Similarly

\[\text{ar(}\Delta \text{ABD})=\text{ar}(\Delta \text{BCD)}\]

(ii) Parallelograms which are on the same base and between the same parallel lines are equal in area.

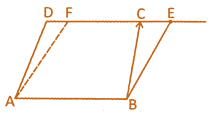
In the above given figure,

\[ar(l{{l}^{gm}}ABCD)=ar(l{{l}^{gm}}ABEF)\]

(iii) Triangles which are on the same base and between the same parallel lines are equal in area.

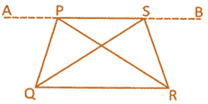
In the above given figure \[QR|\,\,|AB\]

Then \[~\text{ar(}\Delta \text{PQR)}=\text{ar(}\Delta \text{QRS)}\]

(iv) Area of trapezium= \[\frac{1}{2}\] (sum of parallel sides) \[\times \] (distance between them)    

• A quadrilateral is known as a concave quadrilateral if one interior angle is reflex.                     
• A self-intersecting quadrilateral is called a cross-quadrilateral, butterfly quadrilateral or bow-tie quadrilateral.           
• A non-planar quadrilateral is called a skew quadrilateral.    

• The sum of all interior angles of a quadrilateral is\[{{360}^{o}}\].
• In a parallelogram opposite sides and opposite angles are equal and diagonals bisect each other.         
• If a transversal intersect three and more than three parallel lines in such a way that all the intercepts are equal, then the intercept on any other transversal is also equal.
• Parallelograms which one on the same base and between the same parallel lines are equal in area.
• Triangles which are on the same base and between same parallel lines are equal in area.              

  In the figure given below shows a pentagon in which TU drawn parallel to SP meet at QP produced at U and RV parallel to SQ, meet PQ produced at V then:

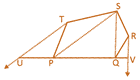
(a) ar(pentagon PQRST) \[=\text{ar(}\Delta \text{STU)}+\text{ar(}\Delta \text{QRV)}\]

(b) ar(pentagon PQRST) \[~=\text{ar(}\Delta \text{SUV)}\]

(c) ar(pentagon PQRST) \[~=\text{ar(}\Delta \text{SUV)}+\text{ar(}\Delta \text{TUP)}\]

(d) ar(pentagon PQRST) \[=\text{ar}(\Delta \text{SUV})+\text{ar(}\Delta \text{QRV)}\]

(e) None of these  

Answer: (b)

Explanation:

Since \[RV|\,|SQ\] \[\Rightarrow \] \[~\text{ar(}\Delta \text{SPT)}=\text{ar}(\Delta \text{TUP)}\]

\[\text{ar(}\Delta \text{SQR)}+\text{ar(}\Delta \text{SPT)}+\text{ar(}\Delta \text{SPQ)}=\text{ar(}\Delta \text{SRV)}+\]\[\text{ar(}\Delta \text{SUP)}+\text{ar(}\Delta \text{BPQ)}\]

\[\Rightarrow \] \[\text{ar(pentagon PQRST)}=\text{ar(}\Delta \text{SUV)}\]

  In a trapezium non-parallel sides are equal. When we join the midpoint of diagonals and parallel sides a quadrilateral is formed, the quadrilateral formed is.....

(a) Rhombus                                     

(b) Rectangle

(c) Trapezium                                   

(d) Square

(e) None of these

Answer: (b)  

  For a trapezium which one of the following statements is correct?

(a) Adjacent sides are parallel

(b) Vertically opposite sides are parallel

(c) The line joining the mid points of the diagonal is parallel to the parallel side and equal to half their differences

(d) The line joining the mid points of the diagonal is parallel to the parallel side and equal to their differences

(e) None of these

Answer: (b)  

  If the length of the diagonals of rhombus are 30 cm and 16 cm respectively then the perimeter of rhombus is_____.

(a) 17cm                              

(b) 69cm

(c) 63cm                              

(d) 68cm

(e) None of these

Answer: (d)  

  In the adjoining figures which have equal value of angle\[x\]? [Every quadrilateral is rhombus]

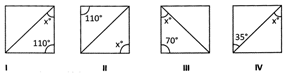
(a) I and II                                           

(b) II and III

(c) III and IV                                       

(d) I and IV

(e) None of these  

Answer: (d)