Some Important Results
Category : 9th Class
Some Important Results
(i) The longer side of a triangle has greater angle opposite to it.
(ii) The greater angle of a triangle has longer side opposite to it.
(iii) Perpendicular line segment is the shortest in length. PM is the shortest line segment from point P to line I.
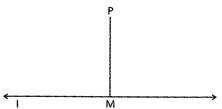
(iv) The distance between line and points lying on it is always zero.
(v) The sum of any two sides of a triangle is greater than the third side.
(vi) The difference between any two sides of a triangle is always less than its third side.
The quadrilateral which is formed by joining the mid points of a given quadrilateral is always_______.
(a) A parallelogram
(b) A trapezium
(c) A rhombus
(d) A rectangle
(e) None of these
Answer: (a)
Explanation:
Given:
A quadrilateral LMNO is a quadrilateral in which P, Q, R and S are the mid points of LM, MN, NO, OL respectively.
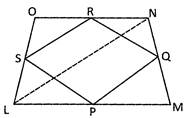
To Prove:
PQRS is a parallelogram
Construction:
Join LN
Proof:
In\[\Delta \text{LMN}\],
\[PQ\,|\,\,|\,LN\] and \[\text{PQ}=\frac{1}{2}\text{LN}\] ...,.(i)
[Because P and Q are the mid points of LM and MN respectively]
In \[\Delta \text{LNO}\]
\[SR\,|\,\,|LN\] and \[\text{SR}=\frac{1}{2}\text{LN}\] .....(ii)
[Because S and R are the mid - points of LO and ON respectively]
From (i) and (ii), we get
\[\text{PQ}=\text{SR}\] and \[~\text{PQ}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{SR}\] ....(iii)
Similarly we can see that
\[\text{PS}=\text{QR}\] and \[\text{PS}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{QR}\] .....(iv)
From (iii) and (iv), we conclude that quadrilateral PQRS is a parallelogram.
In \[\Delta \text{LMN}\] which LP is the bisector of MN and BR is the bisector of LP. Here, points P and R are the points of line segment MN and LN respectively then is equal to.... .
(a) \[\frac{2}{3}LN\]
(b) \[\frac{1}{3}LN\]
(c) \[\frac{2}{3}LM\]
(d) \[\frac{1}{3}LM\]
(e) None of these
Answer: (b)
Explanation:
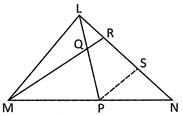
Let the Q is the midpoint of LP
Draw a line \[PS\,|\,\,|\,MR\] since P is the midpoint of MN
\[\Rightarrow \]S is the midpoint of RN
In\[\Delta \text{LPN}\],
\[QR\,|\,\,|\,\,PS\]
\[\Rightarrow \] R is the midpoint of \[LS\] \[\Rightarrow \]\[LR=RS=SN\] \[\Rightarrow \]\[LR=\frac{1}{3}(LN)\]
In the figure given below \[\text{ON}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{LM}\]
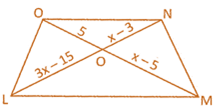
the value of\[x\]is.....
(a) 5, 11
(b) 5, 8
(c) 8, 5
(d) 18, 5
(e) None of these
Answer: (d)
In the given \[\Delta \text{DEF},\text{ GH }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ EF}\] and if \[\frac{DG}{GE}=\frac{3}{5}\] and DF = 5.6 cm then the value of DE is equal to..... .
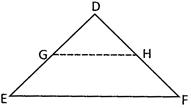
(a) 2.1cm
(b) 3.36cm
(c) 9.35cm
(d) 2.24cm
(e) None of these
Answer: (a)
In a trapezium PQRS, PQ||RS. If the diagonal PR and QS intersect at a point 0 such that OP = 6 cm and OR = 8 cm, then the ratio of ar(\[\Delta \text{POQ}\]) and ar (\[\Delta ROS\]) is equal to:
(a) \[\frac{3}{4}\]
(b) \[\frac{36}{48}\]
(c) \[\frac{9}{16}\]
(d) \[\frac{5}{16}\]
(e) None of these
Answer: (c)
If the midpoint of the hypotenuse is joined with the vertex of a right angled triangle where the right angle formed then the length of this line segment is:
(a) \[\frac{1}{2}\] of the base
(b) \[\frac{1}{2}\] of the perpendicular
(c) \[\frac{1}{2}\] of the hypotenuse
(d) \[\frac{1}{2}\] of the area of triangle
(e) None of these
Answer: (c)
Explanation:
Given:
The figure given below represents all the conditions S is the midpoint of PR,
To prove:
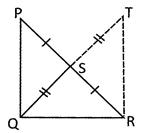
Construction:
Produce QS to T; so that QS = ST and Join RT.
Proof:
In\[\Delta \text{PSQ}\] and \[\Delta \text{RST}\] \[\text{PS}=\text{SR}\] (S is the mid point of PR)
\[\text{QS}=\text{ST}\] (By construction)
\[\angle \text{PSQ}=\angle \text{TSR}\] (Vertically opposite angles)
\[\therefore \]\[\Delta \text{PSQ}=\Delta \text{RST}\] (By S-A-S criteria)
\[\therefore \]\[\text{PQ}=\text{RT}\]and\[\angle \text{QPR}=\angle \text{PRT}\] (Alternate interior angles)
\[\Rightarrow \]\[\text{RT}\,\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }\,\text{PQ}\] \[\Rightarrow \]\[\angle \text{TRQ}=\text{9}0{}^\circ \]
Now in\[\Delta \text{PQR}\]and\[\Delta \text{TRQ}\]
\[\text{QR}=\text{QR}\] (Common side)
\[\text{PQ}=\text{RT}\] (Already proved)
\[\therefore \] \[\Delta PQR\cong \Delta TRS\] (By R-H-S criteria)
\[\Rightarrow \]\[PR=QT\]\[\Rightarrow \]\[\frac{1}{2}QT=\frac{1}{2}PR\]
In the figure given below:
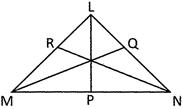
LP, MQ and NR are the median of \[\Delta \text{LMN}\] then which one of the following conditions is correct?
(a) \[(\text{LM}+\text{MN}+\text{NP})<(\text{LP}+\text{MQ}+\text{NR})\]
(b) \[\text{(LM}+\text{MN}+\text{NP})>(\text{NP}+\text{MQ}+\text{NR})\]
(c) \[\text{(LM}+\text{MN}+\text{NP})>(\text{LP}+\text{MQ}+\text{NR)}\]
(d) \[\text{(L}{{\text{M}}^{2}}+\text{M}{{\text{N}}^{2}}+\text{N}{{\text{P}}^{2}})>(\text{L}{{\text{P}}^{2}}+\text{M}{{\text{Q}}^{2}}+\text{N}{{\text{R}}^{2}}\text{)}\]
(e) None of these
Answer: (c)
One pair of vertically opposite angles of a quadrilateral are a and b respectively as shown in the figure.
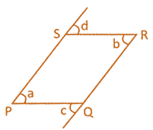
Then which one of the following relations is correct?
(a) \[\text{a}+\text{b}=\text{c}+\text{d}\]
(b) \[\text{a}-\text{b}=\text{c}+\text{d}\]
(c) \[\text{a}+\text{b}=\text{c}-\text{d}\]
(d) \[\text{a}+\text{b}+\text{c}+\text{d}=\text{36}0{}^\circ \]
(e) None of these
Answer: (a)
In the figure given below:
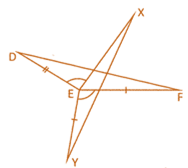
\[\angle \text{DEX}=\angle \text{YEX},\text{ DE}=\text{EX}\] and \[\text{EX}=\text{EF}\] then XY is equal to.....
(a) \[\angle \text{DEX}\]
(b) DF
(c) \[\angle \text{XEF}\]
(d) EF
(e) None of these
Answer: (b)
The line segment PQ and RS intersect each other at point 0 in such a way that OP = OS and OQ = OR then which one of the following options is correct?
(a) PR = SQ and \[~\text{PR }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ SQ}\]
(b) OP=OQ and \[~\text{PR}\bcancel{\text{ }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ }}\text{SQ}\]
(c) RO = OS and\[~\text{PR }\!\!|\!\!\text{ }\,\,\text{ }\!\!|\!\!\text{ SQ}\]
(d) PR = SQ and PR and SQ may or may not be parallel to each other
(e) None of these
Answer: (d)
You need to login to perform this action.
You will be redirected in
3 sec
