10th Class Mathematics Introduction to Trigonometry Question Bank

done Case Based (MCQs) - Introduction to Trigonometry Total Questions - 35

• question_answer1)

  Direction: Q. 1 to 5

  Anika is studying in X standard. She is making a figure to understand trigonometric ratio shown as below.

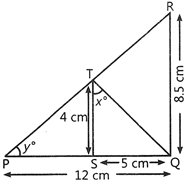
  In \[\Delta PQR,\] \[\angle Q\] is right angled, \[\Delta QTR\]is right angled at T and \[\Delta QST\] is right angled at S. \[PQ=12cm,\] \[QR=8.5cm,\] \[\text{ST}=\text{4 cm},\] \[\text{SQ}=5\text{ cm},\] \[\angle QTS=x{}^\circ \]and\[\angle TPQ=y{}^\circ \]. Give answers to her questions by looking at the figure.

  Based on the above information give the answer of the following questions:

  The length of PT is:
  A)
  \[8\, cm\] done clear
  B)
  \[\sqrt{65}\,cm\] done clear
  C)
  \[7.5\,cm\] done clear
  D)
  \[\sqrt{69}\,cm\] done clear
  View Solution play_arrow

• question_answer2)
  The value of \[\tan x{}^\circ \] is:
  A)
  \[\frac{7.5}{13}\] done clear
  B)
  \[\frac{5}{4}\] done clear
  C)
  \[\frac{4}{5}\] done clear
  D)
  \[\frac{13}{7.5}\] done clear
  View Solution play_arrow

• question_answer3)
  The value of \[\sec x{}^\circ \] is:
  A)
  \[\frac{\sqrt{91}}{6}\] done clear
  B)
  \[\frac{\sqrt{71}}{6}\] done clear
  C)
  \[\frac{\sqrt{41}}{4}\] done clear
  D)
  \[\frac{\sqrt{31}}{5}\] done clear
  View Solution play_arrow

• question_answer4)
  The value of \[\sin y{}^\circ \] is:
  A)
  \[\frac{4}{\sqrt{65}}\] done clear
  B)
  \[\frac{4}{7}\] done clear
  C)
  \[\frac{7}{4}\] done clear
  D)
  \[\frac{\sqrt{65}}{7}\] done clear
  View Solution play_arrow

• question_answer5)
  The value of \[\cot y{}^\circ \] is:
  A)
  \[\frac{7}{4}\] done clear
  B)
  \[\frac{4}{7}\] done clear
  C)
  \[\frac{\sqrt{65}}{4}\] done clear
  D)
  \[\frac{\sqrt{65}}{7}\] done clear
  View Solution play_arrow

• question_answer6)

  Direction: Q. 6 to 10

  A sailing boat with triangular masts is shown below. Two right triangles can be observed. Triangles PQR and PQS.  both right-angled at Q. The distance \[\text{QR}=\text{2 m}\] and \[\text{QS}=\text{3 m}\] and height \[\text{PQ}=\text{5 m}\].

  Based on the above information, give the answer of the following questions:

  The value of sec S is:
  A)
  \[\frac{\sqrt{34}}{5}\] done clear
  B)
  \[\frac{\sqrt{34}}{3}\] done clear
  C)
  \[\frac{5}{3}\] done clear
  D)
  \[\frac{3}{\sqrt{34}}\] done clear
  View Solution play_arrow

• question_answer7)
  The value of cosec R is:
  A)
  \[\frac{\sqrt{29}}{5}\] done clear
  B)
  \[\frac{\sqrt{29}}{2}\] done clear
  C)
  \[\frac{2}{5}\] done clear
  D)
  \[\frac{5}{\sqrt{29}}\] done clear
  View Solution play_arrow

• question_answer8)
  The value of \[\tan S+\cot R\] is:
  A)
  \[\frac{9}{4}\] done clear
  B)
  \[\frac{5}{3}\] done clear
  C)
  \[\frac{2}{5}\] done clear
  D)
  \[\frac{31}{15}\] done clear
  View Solution play_arrow

• question_answer9)
  Value of \[{{\sin }^{2}}R-{{\cos }^{2}}S\] is:
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[\frac{97}{85}\] done clear
  D)
  \[\frac{589}{986}\] done clear
  View Solution play_arrow

• question_answer10)
  Value of \[{{\sin }^{2}}S-{{\cos }^{2}}R\] is:
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[\frac{97}{85}\] done clear
  D)
  \[\frac{589}{986}\] done clear
  View Solution play_arrow

• question_answer11)

  Direction: Q. 11 to 15

  Three friends - Sanjeev, Amit and Digvijay are playing hide and seek in a park. Sanjeev and Amit hide in the shrubs and Digvijay have to find both of them. If the positions of three friends are at A, B and C respectively as shown in the figure and forms a right angled triangle such that \[\text{AB}=\text{9 m},\] \[\text{BC}=3\sqrt{3}\text{ m}\] and \[\angle B=90{}^\circ \].

  Based on the above information, give the answer of the following questions:

  The measure of \[\angle A\] is:
  A)
  \[30{}^\circ \] done clear
  B)
  \[45{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer12)
  The measure of \[\angle C\] is:
  A)
  \[30{}^\circ \] done clear
  B)
  \[45{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer13)
  The length of AC is:
  A)
  \[2\sqrt{3}\,m\] done clear
  B)
  \[\sqrt{3}\,m\] done clear
  C)
  \[4\sqrt{3}\,m\] done clear
  D)
  \[6\sqrt{3}\,m\] done clear
  View Solution play_arrow

• question_answer14)
  \[\cos 2A=\]
  A)
  \[0\] done clear
  B)
  \[\frac{1}{2}\] done clear
  C)
  \[\frac{1}{\sqrt{2}}\] done clear
  D)
  \[\frac{\sqrt{3}}{2}\] done clear
  View Solution play_arrow

• question_answer15)
  \[\sin \left( \frac{C}{2} \right)=\]
  A)
  \[0\] done clear
  B)
  \[\frac{1}{2}\] done clear
  C)
  \[\frac{1}{\sqrt{2}}\] done clear
  D)
  \[\frac{\sqrt{3}}{2}\] done clear
  View Solution play_arrow

• question_answer16)

  Direction: Q. 16 to 20

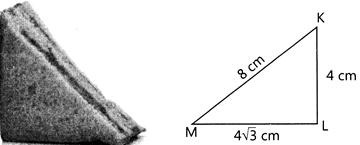
  Priyanshi's daughter is feeling hungry so she thought of eating something. She looked into the fridge and found some bread pieces. She decided to make a sandwich. She cut the piece of bread diagonally and found that it forms a right angled triangle, with sides \[\text{4 cm},\] \[\text{4}\sqrt{3}\text{ cm}\]and\[\text{8 cm}\].

  Based on the above information, give the answer of the following questions:

  The value of \[\angle M=\]
  A)
  \[30{}^\circ \] done clear
  B)
  \[60{}^\circ \] done clear
  C)
  \[45{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer17)
  The value of \[\angle K=\]
  A)
  \[45{}^\circ \] done clear
  B)
  \[30{}^\circ \] done clear
  C)
  \[60{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer18)
  Find the value of sec M.
  A)
  \[\sqrt{3}\] done clear
  B)
  \[\frac{2}{\sqrt{3}}\] done clear
  C)
  \[1\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer19)
  \[{{\sec }^{2}}M-1=\]
  A)
  \[\tan M\] done clear
  B)
  \[\tan 2M\] done clear
  C)
  \[{{\tan }^{2}}M\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer20)
  The value of \[\frac{{{\tan }^{2}}45{}^\circ -1}{{{\tan }^{2}}45{}^\circ +1}\]is:
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[2\] done clear
  D)
  \[-1\] done clear
  View Solution play_arrow

• question_answer21)

  Direction: Q. 21 to 25

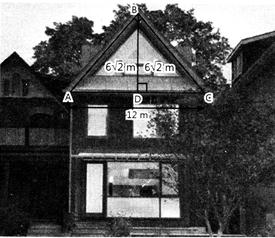
  Soniya and her father went to meet her friend Ruhi for a party. When they reached Ruhi's place, Soniya saw the roof of the house, which is triangular in shape. She imagined the dimensions of the roof as given in the figure.

  s

  Based on the above information, give the answer of the following questions:

  If D is the mid-point of AC, then BD =
  A)
  \[2m\] done clear
  B)
  \[3m\] done clear
  C)
  \[4m\] done clear
  D)
  \[6m\] done clear
  View Solution play_arrow

• question_answer22)
  Measure of \[\angle A=\]
  A)
  \[30{}^\circ \] done clear
  B)
  \[60{}^\circ \] done clear
  C)
  \[45{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer23)
  Measure of \[\angle C=\]
  A)
  \[30{}^\circ \] done clear
  B)
  \[60{}^\circ \] done clear
  C)
  \[45{}^\circ \] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer24)
    Find the value of \[\sin A+\cos C.\]
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[\frac{1}{\sqrt{2}}\] done clear
  D)
  \[\sqrt{2}\] done clear
  View Solution play_arrow

• question_answer25)
  Find the value of \[{{\tan }^{2}}C+{{\tan }^{2}}A\].
  A)
  \[0\] done clear
  B)
  \[1\] done clear
  C)
  \[2\] done clear
  D)
  \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer26)

  Direction: Q. 26 to 30

  In structural design a structure is composed of triangles that are interconnecting. A truss is one of the major types of enginnering structures and is especially used in the design of bridges and buildings. Trusses are designed to support loads, such as the weight of people. A truss is exclusively made of long, straight members connected by joints at the end of each member.

  This is a single repeating triangle in a truss system.

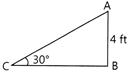  Based on the above information give the, answer of the following questions:

   In above triangle, what is the Length of AC?
  A)
  \[5\,ft\] done clear
  B)
  \[6\,ft\] done clear
  C)
  \[8\,ft\] done clear
  D)
  \[\frac{8}{\sqrt{3}}\,ft\] done clear
  View Solution play_arrow

• question_answer27)
  In above triangle, what is the length of BC?
  A)
  \[5\,ft\] done clear
  B)
  \[6\,ft\] done clear
  C)
  \[8\,ft\] done clear
  D)
  \[4\sqrt{3}\,ft\] done clear
  View Solution play_arrow

• question_answer28)
  If \[\text{sin A}=\text{sin C},\]what will be the length of BC?
  A)
  \[2ft\] done clear
  B)
  \[4ft\] done clear
  C)
  \[8ft\] done clear
  D)
  \[4\sqrt{2}ft\] done clear
  View Solution play_arrow

• question_answer29)
  If \[\sin (A+B)=\frac{1}{\sqrt{2}}\]and \[\cos (A-B)=\frac{\sqrt{3}}{2},\] \[0{}^\circ <A+B\le 90{}^\circ ,\] \[A>B\]then \[\angle A\]is:
  A)
  \[45{}^\circ \] done clear
  B)
  \[37.5{}^\circ \] done clear
  C)
  \[32.5{}^\circ \] done clear
  D)
  \[35{}^\circ \] done clear
  View Solution play_arrow

• question_answer30)
  If the length of AB doubles what will happen to the Length of AC?
  A)
  remains same done clear
  B)
  doubles the original lengthy done clear
  C)
  become three times the original length done clear
  D)
  become half of the original length done clear
  View Solution play_arrow

• question_answer31)

  Direction: Q. 31 to 35

  An electrician wanted to repair a street lamp at a height of 15 feet. He places his ladder such that its foot is 8 feet from the foot of the lamp post as shown in the figure below:

  Based on the above information give the, answer of the following questions:

  The value of \[\cos R\] is:
  A)
  \[\frac{8}{15}\] done clear
  B)
  \[\frac{8}{17}\] done clear
  C)
  \[\frac{15}{8}\] done clear
  D)
  \[\frac{15}{17}\] done clear
  View Solution play_arrow

• question_answer32)
  The value of \[\text{cosec}\,\,\text{P}\] is:
  A)
  \[\frac{8}{17}\] done clear
  B)
  \[\frac{15}{17}\] done clear
  C)
  \[\frac{17}{8}\] done clear
  D)
  \[\frac{17}{15}\] done clear
  View Solution play_arrow

• question_answer33)
  The value of \[\frac{\sin R-\cos P}{\sin R+\cos P}\] is:
  A)
  \[\frac{17}{30}\] done clear
  B)
  \[\frac{30}{17}\] done clear
  C)
  \[0\] done clear
  D)
  \[1\] done clear
  View Solution play_arrow

• question_answer34)
  The value of cot P is:
  A)
  \[\frac{15}{17}\] done clear
  B)
  \[\frac{17}{15}\] done clear
  C)
  \[\frac{8}{15}\] done clear
  D)
  \[\frac{15}{8}\] done clear
  View Solution play_arrow

• question_answer35)
  The value of \[\tan R+\frac{3}{\sec P}-1\]is:
  A)
  \[\frac{253}{136}\] done clear
  B)
  \[\frac{357}{136}\] done clear
  C)
  \[\frac{479}{136}\] done clear
  D)
  \[1\] done clear
  View Solution play_arrow