10th Class Mathematics Pair of Linear Equations in Two Variables Question Bank

done Case Based (MCQs) - Pair of Linear Equations in Two Variables Total Questions - 40

• question_answer1)

  Case Study : Q. 1 to 5

  Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is \[\text{95 sq}.\text{ m}\].

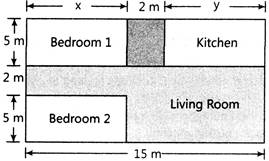  Based on the above information, give the answer of the following questions:

  The pair of linear equations in two variables from this situation are:
  A)
  \[2x+y=19,\,\,x+y=13\] done clear
  B)
  \[x+2y=19,\,\,x+y=18\] done clear
  C)
  \[x+y=19,\,\,x+2y=13\] done clear
  D)
  \[x+3y=19,2\,x+y=15\] done clear
  View Solution play_arrow

• question_answer2)
  Find the perimeter of the outer boundary of the Layout
  A)
  \[45\,m\] done clear
  B)
  \[54m\] done clear
  C)
  \[44m\] done clear
  D)
  \[55m\] done clear
  View Solution play_arrow

• question_answer3)
  Find the area of each bedroom and kitchen in the Layout
  A)
  Area of each bedroom\[=\text{35 sq}.\text{ m}\] Area of kitchen \[=\text{3}0\text{ sq}.\text{ m}\] done clear
  B)
  Area of each bedroom \[=\text{53 sq}.\text{ m}\] Area of kitchen \[=\text{3}0\text{ sq}.\text{ m}\] done clear
  C)
  Area of each bedroom \[=\text{3}0\text{ sq}.\text{ m}\] Area of kitchen \[=\text{35 sq}.\text{ m}\] done clear
  D)
  None of the above   done clear
  View Solution play_arrow

• question_answer4)
  Find the area of living room in the layout
  A)
  \[\text{75 sq}.\text{ m}\] done clear
  B)
  \[\text{57 sq}.\text{ m}\]   done clear
  C)
  \[\text{55 sq}.\text{ m}\] done clear
  D)
  \[\text{77 sq}.\text{ m}\] done clear
  View Solution play_arrow

• question_answer5)
  Find the cost of laying tiles in kitchen at the rate of Rs.50 per sq. m.
  A)
  Rs.1250 done clear
  B)
  Rs.1575 done clear
  C)
  Rs.1700 done clear
  D)
  Rs.1750 done clear
  View Solution play_arrow

• question_answer6)

  Case Study : Q. 6 to 10

  Sanjeev a student of class X, goes to Yamuna river with his friends. When he saw a boat in the river, then he wants to sit in boat. So his all friends are ready to sit with him. In this order, Sanjeev is sitting on a boat which upstream at a speed of \[\text{8 km}/\text{h}\] and downstream at a speed of\[\text{16 km}/\text{h}\]. When Sanjeev is in the boat, some questions are arises in the mind, then answer the given questions.

  The speed of the boat in still water is:
  A)
  \[\text{8 km}/\text{h}\] done clear
  B)
  \[\text{1}0\text{ km}/\text{h}\] done clear
  C)
  \[\text{12 km}/\text{h}\] done clear
  D)
  \[\text{14 km}/\text{h}\] done clear
  View Solution play_arrow

• question_answer7)
  The speed of stream is:
  A)
  \[\text{3 km}/\text{h}\] done clear
  B)
  \[\text{4 km}/\text{h}\] done clear
  C)
  \[\text{5 km}/\text{h}\] done clear
  D)
  \[\text{6 km}/\text{h}\] done clear
  View Solution play_arrow

• question_answer8)
  Which mathematical concept is used in above problem?
  A)
  Pair of linear equations done clear
  B)
  Cross-multiplication method done clear
  C)
  Factorisation method done clear
  D)
  None of the above done clear
  View Solution play_arrow

• question_answer9)
  The direction in which the speed is maximum, is:
  A)
  upstream done clear
  B)
  downstream done clear
  C)
  both have equal speed done clear
  D)
  None of these   done clear
  View Solution play_arrow

• question_answer10)
  The average speed of stream and boat in still water is:
  A)
  \[\text{7 km}/\text{h}\] done clear
  B)
  \[\text{10 km}/\text{h}\]   done clear
  C)
  \[\text{12 km}/\text{h}\] done clear
  D)
  \[\text{5 km}/\text{h}\] done clear
  View Solution play_arrow

• question_answer11)

  Case Study : Q. 11 to 15

  Akhila went to a fair in her village. She wanted to enjoy rides on the giant wheel and play hoopla (a game in which you throw a ring on the items kept in a stall and if the ring covers any object completely you get it). The number of times she played hoopla is half the number of times she rides the giant wheel. If each ride costs Rs.3 and a game of hoopla costs Rs. 4 and she spent Rs. 20 in the fair.

  Based on the given information, give the answer of the following questions.

  The representation of given statement algebraically is:
  A)
  \[\text{x}-\text{2y}=0\]and \[\text{3x}+\text{4y}=\text{2}0\] done clear
  B)
  \[\text{x}+\text{2y}=0\]and \[\text{3x}-\text{4y}=\text{2}0\] done clear
  C)
  \[\text{x}-\text{2y}=0\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear
  D)
  \[None\,\, of\,\, the\,\,above\] done clear
  View Solution play_arrow

• question_answer12)
  Graphically, if the pair of equations intersect at one point, then the pair of equation is:      
  A)
  Consistent done clear
  B)
  inconsistent    done clear
  C)
  consistent or inconsistent done clear
  D)
  None of these  done clear
  View Solution play_arrow

• question_answer13)
  The intersection point of two lines is:
  A)
  \[(-4,-2)\] done clear
  B)
  \[(4,3)\] done clear
  C)
  \[(2,4)\] done clear
  D)
  \[(4,2)\] done clear
  View Solution play_arrow

• question_answer14)
  Intersection points of the line \[x-2y=0\]on x and y-axes are:
  A)
  \[(2,0),\,\,(0,1)\] done clear
  B)
  \[(1,0),\,\,(0,2)\] done clear
  C)
  \[(0,0)\] done clear
  D)
  \[None\,\, of\,\, these\] done clear
  View Solution play_arrow

• question_answer15)
  Intersection points of the line \[\text{3x}+\text{4y}=\text{2}0\]on x and y-axes -are:
  A)
  \[\left( \frac{20}{3},0 \right),\,(0,5)\] done clear
  B)
  \[(2,0),\,\,(0,1)\] done clear
  C)
  \[(5,0),\left( 0,\frac{20}{3} \right)\] done clear
  D)
  \[None\,\, of\,\, these\] done clear
  View Solution play_arrow

• question_answer16)

  Case Study : Q. 16 to 20

  The residents of a group housing society at Jaipur decided to build a rectangular garden to beautify the garden.

  One of the members of the society made some calculations and informed that if the length of the rectangular garden is increased by 2 m and the breadth reduced by 2 m, the area gets reduced by 12 sq. m. If, however, the length is decreased by 1 m and breadth increased by 3 m, the area of the rectangle is increased by.

  Based on the above information, give the answer of the following questions:

  The dimensions of the rectangle are:
  A)
  Length = 6 m, breadth = 4 m done clear
  B)
  length = 10 m, breadth = 6 m done clear
  C)
  length =10 m, breadth =4 m done clear
  D)
  length = 6 m, breadth = 2m done clear
  View Solution play_arrow

• question_answer17)
  If the graphs of the equations in the given situation are plotted on the same graph paper, then:     
  A)
  The lines will be parallel done clear
  B)
  The lines will coincide done clear
  C)
  The lines will intersect done clear
  D)
  Can't say done clear
  View Solution play_arrow

• question_answer18)
  The coordinates of the points where the two Lines, when plotted on a graph paper, intersect the x-axis are:
  A)
  \[(4,0)\] and \[(8,0)\] done clear
  B)
  \[(-4,0)\] and \[(8,0)\] done clear
  C)
   \[(4,0)\]and \[(-8,0)\] done clear
  D)
  \[(-4,0)\] and \[(-8,0)\] done clear
  View Solution play_arrow

• question_answer19)
  The value of k for which the system of equations \[\text{x+y}-\text{4=0}\]and \[\text{2x}+\text{ky}=\text{3}\] has no solution, is:
  A)
  \[-2\] done clear
  B)
  \[\ne 2\] done clear
  C)
  2 done clear
  D)
  3 done clear
  View Solution play_arrow

• question_answer20)
  The equation of a line parallel to the line whose equation is given by \[\text{3x}-\text{2y}=\text{8}\] can be:
  A)
  \[\text{3x}+\text{2y}=8\] done clear
  B)
  \[3x-2y=8\] done clear
  C)
  \[6x+4y=16\] done clear
  D)
  \[15x-10y=45\] done clear
  View Solution play_arrow

• question_answer21)

  Case Study : Q. 21 to 25

  The resident welfare association of a Radheshyam society decided to build two straight paths in their neighbourhood park such that they do not cross each other and also plan trees along the boundary lines of each path.

  One of the members of association Shyam Lal suggested that the paths should be constructed represented by the two linear equations \[\text{x}-\text{3y}=\text{2}\]and\[-\text{2x+6y}=\text{5}\].

  Based on the above information, give the answer of the following questions.

  If the pair of equations \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\] has infinitely solutions, then condition is:
  A)
  \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\] done clear
  B)
  \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\] done clear
  C)
  \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\] done clear
  D)
  \[None\,\, of\,\, these\] done clear
  View Solution play_arrow

• question_answer22)
  If pair of lines are parallel, then pair of linear equations is:
  A)
  inconsistent  done clear
  B)
  consistent done clear
  C)
  consistent or inconsistent done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer23)
  Check weather the two paths will cross each other or not.
  A)
  yes done clear
  B)
  no done clear
  C)
  do not say done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer24)
  How many point(s) lie on the Line \[\text{x}-\text{3y}=\text{2}\]?
  A)
  one done clear
  B)
  two done clear
  C)
  three done clear
  D)
  infinitely done clear
  View Solution play_arrow

• question_answer25)
  If the line \[\text{2x}+\text{6y}=\text{5}\] intersect the X-axis, then find its coordinate.
  A)
  \[(-2.5,0)\] done clear
  B)
  \[(2.5,0)\] done clear
  C)
  \[(0,2.5)\] done clear
  D)
  \[(0,-2.5)\] done clear
  View Solution play_arrow

• question_answer26)

  Case Study : Q. 26 to 30

  Gagan went to a local mela. He ate several rural delicacies such as jalebis, chaat etc. He also wanted to play the ring game in which a ring is thrown on the items displayed on the table and the balloon shooting game.

  The cost of three balloon shooting games exceeds the cost of four ring games by Rs. 4. Also, the total cost of three balloon shooting games and four ring games is Rs.20.

  Based on the given information, answer the following questions:

  Taking the cost of one ring game to be Rs.x and that of one balloon game as Rs.y, the pair of linear equations describing the above:
  A)
  \[-\text{4x}-\text{3y}=-\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear
  B)
  \[\text{4x}-\text{3y}=\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear
  C)
  \[\text{4x}-\text{3y}=-\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear
  D)
  \[-\text{4x}+\text{3y}=-\text{4}\]and \[\text{4x}+\text{3y}=\text{2}0\] done clear
  View Solution play_arrow

• question_answer27)
  The cost of one ring game and one balloon game is:
  A)
  Rs.2and Rs.4 done clear
  B)
  Rs.4 and Rs.2 done clear
  C)
  Rs.8 and Rs.2 done clear
  D)
  Rs.6 and Rs.3 done clear
  View Solution play_arrow

• question_answer28)
  The points where the line represented by the equation \[\text{4x}-\text{3y}=-\text{ 4}\] intersects the x-axis and y-axis, respectively are given by:
  A)
  \[(1,0),\,\,\left( 0,\frac{4}{3} \right)\] done clear
  B)
  \[(1,0),\,\,\left( 0,\frac{4}{3} \right)\] done clear
  C)
  \[(-1,0),\,\,\left( 0,-\frac{4}{3} \right)\] done clear
  D)
  \[(1,0),\,\,\left( 0,-\frac{4}{3} \right)\] done clear
  View Solution play_arrow

• question_answer29)
  The area of the triangle formed by the two lines and the x-axis is:
  A)
  4 sq. units done clear
  B)
  6 sq. units done clear
  C)
  8 sq. units done clear
  D)
  12 sq. units done clear
  View Solution play_arrow

• question_answer30)
  The value of k for which the pair of linear equations \[-x+y=-1,\] \[x+ky=5\] will be inconsistent, is:        
  A)
  \[k=1\] done clear
  B)
  \[k=-1\] done clear
  C)
  \[k\ne -1\] done clear
  D)
  \[k\ne 1\] done clear
  View Solution play_arrow

• question_answer31)

  Case Study : Q. 31 to 35

  Mr Gaurav decided to go to a amusement park along with his family. The cost of a entry ticket is Rs. 25.00 for children and Rs.50.00 for adults. On that particular day, attendance at the circus is 2,000 and the total gate revenus is Rs. 70,000.

  Based on the given information, give the answer of the following questions:

  If we let the number of children and adults who bought ticket on that day as x and y respectively, form the pair of Linear equations describing the above situation are given as:
  A)
  \[\text{x}+\text{ y}=\text{2}000\]and \[x+2y=2800\] done clear
  B)
  \[\text{x}+\text{2y}=\text{2}000\]and \[\text{x}+\text{y}=\text{28}00\] done clear
  C)
  \[\text{2x}+\text{y}=\text{2}000\]and \[\text{x}+\text{y}=\text{28}00\] done clear
  D)
  \[\text{x}+y=\text{2}000\]and \[\text{2x}+\text{y}=\text{28}00\] done clear
  View Solution play_arrow

• question_answer32)
  Find the number of children and adults who bought tickets on that particular day are:
  A)
  1100 and 900 done clear
  B)
  1200 and 800 done clear
  C)
  1300 and 700 done clear
  D)
  1500 and 300 done clear
  View Solution play_arrow

• question_answer33)
  Find the value(s) of k for which the pair of linear equations given by \[\text{2x}+\text{5y}=\text{2};\] \[(k+2)x+(2k+1)y=2(k-1)\] will have infinitely many solutions.
  A)
  \[6\] done clear
  B)
  \[-4\] done clear
  C)
  \[4\] done clear
  D)
  \[-6\]   done clear
  View Solution play_arrow

• question_answer34)
  Find the points where the lines represented by the equations \[\text{2x}-\text{5y}+\text{4}=0\]and \[\text{x}+\text{2y}-\text{5}=0\]respectively intersect the x-axis.
  A)
  \[(-3,0)\] and \[(4,0)\] done clear
  B)
  \[(-2,0)\] and \[(5,0)\] done clear
  C)
  \[(-1,0)\] and \[(6,0)\] done clear
  D)
  \[(2,0)\] and \[(4,0)\] done clear
  View Solution play_arrow

• question_answer35)
  Write the number of solutions of the system of linear equations \[\text{2x}-\text{3y}+\text{4}=0\] and \[\text{x}+\text{2y}-\text{5=0}\].
  A)
  1 done clear
  B)
  2 done clear
  C)
  0 done clear
  D)
  infinite done clear
  View Solution play_arrow

• question_answer36)

  Case Study : Q. 36 to 40

  A test consists of True' or 'False' questions. One mark is awarded for every correct answer while \[\frac{1}{4}\] mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answer 120 questions and got 90 marks.

  Type of Question     Marks given for correct answer        Marks deducted for wrong answer True/False 1 0.25 Based on the above information, give the answer of the following questions:

  If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?
  A)
  24 done clear
  B)
  96 done clear
  C)
  70 done clear
  D)
  100 done clear
  View Solution play_arrow

• question_answer37)
  How many questions did he guess?
  A)
  24 done clear
  B)
  70       done clear
  C)
  100 done clear
  D)
  96 done clear
  View Solution play_arrow

• question_answer38)
  If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?
  A)
  96 done clear
  B)
  24 done clear
  C)
  100 done clear
  D)
  70 done clear
  View Solution play_arrow

• question_answer39)
  If answer to all questions be attempted by guessing were wrong, then how many questions answered correctly to score 90 marks?
  A)
  24 done clear
  B)
  70 done clear
  C)
  96 done clear
  D)
  100 done clear
  View Solution play_arrow

• question_answer40)
  If answer to all questions he attempter by guessing were wrong and answered \[\text{5}0%\]correctly, then how many marks he got?
  A)
  45 done clear
  B)
  55       done clear
  C)
  65 done clear
  D)
  40 done clear
  View Solution play_arrow