question_answer 1)
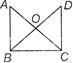
In the given figure, \[\Delta ABC\tilde{\ }\Delta DCB,\] then \[AB\times DB=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 2)
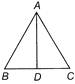
In an isosceles triangle ABC, \[AC=BC,\]\[\angle BAC\]is bisected by AD where D lies on BC. It is found that \[AD=AB.\] Then \[\angle ACB\]equals
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 3)
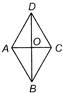
In rhombus ABCD \[A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+D{{A}^{2}}=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 4)
In the given figure, \[\angle BAC=\angle ADC,\] then \[CA/CB\] is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 5)
In the given adjacent figure, BA and BC are produced to meet CD and AD produced in E and F. Then \[\angle AED+\angle CFD=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 6)
P and Q are points on sides AB and AC respectively of \[\Delta ABC.\] If \[AP=3\,cm,\] \[PB=6\,cm,\] \[AQ=5\,cm\] and \[QC=10\,cm,\] then BC=
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 7)
In the given figure, \[AD\bot BC,\] \[BE\bot AC,\]\[CF\bot AB,\] then \[A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 8)
In \[\Delta ABC,\] \[AB=AC\] and D is a point on side AC, such that \[B{{C}^{2}}=AC\times CD\] then BD=
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 9)
ABC is right triangle right angled at C. If p is the length of the perpendicular from C to AB and a, b, c have the usual meaning, then \[\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 10)
In the given \[\Delta ABC,\] \[AD\bot BC\]and \[\angle A\] is right angled. Then \[A{{D}^{2}}=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 11)
In the given figure, \[AB||PQ||CD,\]\[AB=x\] units, \[CD=y\] units and \[PQ=z\] units, then \[\frac{1}{x}+\frac{1}{y}=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 12)
\[\Delta ABC\] is such that \[AB=3cm,\] \[BC=2cm\] and \[CA=2.5cm.\] If \[\Delta DEF\tilde{\ }\Delta ABC\] and \[EF=4cm,\] then perimeter of \[\Delta DEF\] is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 13)
In the given figure, \[\angle ABC={{90}^{o}}\] and \[BD\bot AC.\] If \[BD=8cm,\]\[AD=4cm,\] then CD=
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 14)
In the given trapezium ABCD, \[AB||CD\] and \[AB=2CD.\] If area of \[\Delta AOB=84c{{m}^{2}},\] then the area of \[\Delta COD\] is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 15)
In an isosceles \[\Delta \,ABC,\] \[AB=AC\] and \[BD\bot AC\] then \[(B{{D}^{2}}-C{{D}^{2}})=\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 16)
If a tree casts a 18 feet shadow and at the same time, a child of height 3 feet casts a 2 feet shadow, then the height the tree is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 17)
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, then the distance between their tops is ;
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 18)
A 12 cm rod is held between a flashlight and a wall as shown. Find the length of the shadow on the wall if the rod is 45 cm from the wall and 15 cm from the light.
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 19)
. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after \[1\frac{1}{2}\] hours?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 20)
Mason Construction wants to connect two parks on opposite sides of town with a road. Surveyors have laid out a map as shown. The road can be built through the town or around town through point R. The roads intersect at a right angle at point R. The line joining Park A to Park B is parallel to the line joining C and D.
(i) What is the distance between the parks through town? (ii) What is the distance from Park A to Park B through point R?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 21)
In the given figure, ABC is a right triangle right-angled at B. AD and CE are the two medians drawn from A and C respectively. If \[AC=5\text{ }cm\]and \[AD=\frac{3\sqrt{5}}{2}cm,\]then the length of CE is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 22)
Match the following.
Column-l Column-ll (P) In \[\Delta \,ABC\] and \[\Delta \,PQR\] \[\frac{AB}{PQ}=\frac{AC}{PR},\angle A=\angle P\]\[\Rightarrow \] \[\Delta ABC\tilde{\ }\Delta PQR\] (1) AA similarity criterion (Q) In \[\Delta ABC\] and \[\Delta PQR\] \[\angle A=\angle P,\angle B=\angle Q\] \[\Rightarrow \] \[\Delta \,ABC\tilde{\ }\Delta PQR\] (2) SAS similarity criterion (R) In \[\Delta \,ABC\] and \[\Delta \,PQR\] \[\frac{AB}{PQ}=\frac{AC}{PR}=\frac{BC}{QR}\] \[\Rightarrow \] \[\Delta \,ABC\tilde{\ }\Delta PQR\] (3) SSS similarity criterion (S) In \[\Delta \,ABC\], \[DE||BC\] \[\Rightarrow \] \[\frac{AD}{BD}=\frac{AE}{CE}\] (4) BPT
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 23)
Which of the following statements is CORRECT?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 24)
P and O are the mid-points of the sides CA and CB respectively of a \[\Delta \,ABC,\] right angled at C, then find :
(i) \[4A{{C}^{2}}+B{{C}^{2}}\] (ii) \[4B{{C}^{2}}+A{{C}^{2}}\] (iii) \[4(A{{Q}^{2}}+B{{P}^{2}})\]
A)
B)
C)
D)
View Solution play_arrow
question_answer 25)
In the given figure, the line segment XY is parallel to side AC of \[\Delta \,ABC\] and it divides the triangle into two parts of equal area. Then, find
(i) \[AX:AB\] (ii) \[\frac{AC}{XY}\]
A)
B)
C)
D)
View Solution play_arrow