9th Class Mathematics Areas of Parallelograms and Triangles Question Bank

done Area of Parallelogram & Triangle Total Questions - 30

• question_answer1)
  The difference of the areas of two squares drawn on two line segments of different lengths is 51 sq. cm. Find the length of the greater line segment if one is longer than the other by 3 cm.
  A)
   7 cm                            done clear
  B)
   9 cm done clear
  C)
   11 cm                          done clear
  D)
   16 cm done clear
  View Solution play_arrow

• question_answer2)
  A kite in the shape of a square with a diagonal 32 cm attached to an equilateral triangle of the base 8 cm. Approximately how much paper has been used to make it? (use\[\sqrt{3}=\mathbf{1}.\mathbf{732}\])
  A)
   539.712 \[c{{m}^{2}}\]       done clear
  B)
   538.721 \[c{{m}^{2}}\] done clear
  C)
   540.712 \[c{{m}^{2}}\]                       done clear
  D)
   539.217 \[c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer3)
  A field is in the shape of a trapezium whose parallel sides are 25m and 10m. The non parallel sides are 14m and 13m. Then the area of the field is
  A)
   190 \[{{m}^{2}}\]                   done clear
  B)
   180 \[{{m}^{2}}\]          done clear
  C)
   196 \[{{m}^{2}}\]  done clear
  D)
   195 \[{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer4)
  The area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m, is
  A)
   380 \[{{m}^{2}}\]                               done clear
  B)
   370\[{{m}^{2}}\] done clear
  C)
   374 \[{{m}^{2}}\]                               done clear
  D)
   384\[{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer5)
  The length of a room floor exceeds its breadth by 20 m. The area of the floor remains unaltered when the length is decreased by 10 m but the breadth is increased by 5 m. The area of the floor (in square metres) is
  A)
   280                            done clear
  B)
   325 done clear
  C)
   300    done clear
  D)
   420 done clear
  View Solution play_arrow

• question_answer6)
  The length and breadth of a rectangle are increased by 20 % and 10% respectively. The increase in the area of the resulting rectangle will be
  A)
   60%                            done clear
  B)
   50% done clear
  C)
   40%                            done clear
  D)
   32% done clear
  View Solution play_arrow

• question_answer7)
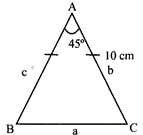
  In the given figure an isosceles triangle, the measure of each of equal sides is 10 cm and the angle between them is 45°, the area of the triangle is
  A)
   25 \[c{{m}^{2}}\]                   done clear
  B)
   \[\frac{25}{2}\sqrt{2}\,c{{m}^{2}}\] done clear
  C)
   \[25\sqrt{2}\]\[c{{m}^{2}}\]     done clear
  D)
   \[25\sqrt{3}\]\[c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer8)
  ABC is an equilateral triangle of side 4 cm. with A, B, C as vertex and radius 2 cm three arcs are drawn. The area of the region within the triangle bounded by the three area is
  A)
   \[\left( 3\sqrt{3}-\frac{\pi }{2} \right)\]\[c{{m}^{2}}\]      done clear
  B)
   \[\left( \sqrt{3}-\frac{3\pi }{2} \right)\]\[c{{m}^{2}}\] done clear
  C)
   \[4\left( \sqrt{3}-\frac{\pi }{2} \right)\]\[c{{m}^{2}}\] done clear
  D)
   \[\left( \frac{\pi }{2}-\sqrt{3} \right)\]\[c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer9)
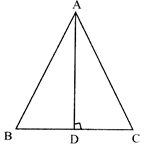
  The area of an isosceles triangle is 4 square unit. If the length of the third side is 4 unit, the length of each equal side is
  A)
   4 units                          done clear
  B)
   \[2\sqrt{3}\]units        done clear
  C)
   \[2\sqrt{2}\]units     done clear
  D)
   \[3\sqrt{2}\]units done clear
  View Solution play_arrow

• question_answer10)
  A parallelogram has sides 15 cm and 7 cm long. The length of one of the diagonals is 20 cm. The area of the parallelogram is
  A)
   42 \[c{{m}^{2}}\]                   done clear
  B)
   60 \[c{{m}^{2}}\]         done clear
  C)
   84 \[c{{m}^{2}}\]        done clear
  D)
   96 \[c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer11)
  Sides of a parallelogram are in the ratio 5 : 4. Its area is 1000 sq. units. Altitude on the greater side is 20 units. Altitude on the smaller side is
  A)
   30 units                        done clear
  B)
   25 units    done clear
  C)
   10 units           done clear
  D)
   15 units done clear
  View Solution play_arrow

• question_answer12)
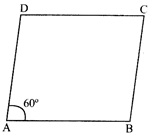
  The perimeter of a rhombus is 16 cm and the measure of an angle is \[60{}^\circ ,\] then the area of it is
  A)
   \[100\sqrt{3}\]\[c{{m}^{2}}\]   done clear
  B)
   \[8\sqrt{3}\]\[c{{m}^{2}}\] done clear
  C)
   \[160\sqrt{3}\]\[c{{m}^{2}}\]               done clear
  D)
   100 \[c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer13)
  If the side of a square is increased by 20%, then its area is increased by :
  A)
   25%                             done clear
  B)
   55% done clear
  C)
   44 %     done clear
  D)
   56.25% done clear
  View Solution play_arrow

• question_answer14)
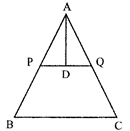
  ABC is an equilateral triangle. P and Q are two points on \[\overline{\mathbf{AB}}\] and \[\overline{\mathbf{AC}}\] respectively such that\[\mathbf{PQ}\parallel \mathbf{BC}\]. If \[\overline{\mathbf{PQ}}=\mathbf{3}\]cm, then area of \[\Delta \mathbf{APQ}\] is:
  A)
   \[\frac{25}{4}\]sq.cm                done clear
  B)
   \[\frac{25}{\sqrt{3}}\]sq.cm done clear
  C)
   \[\frac{9\sqrt{3}}{4}\]sq.cm   done clear
  D)
   \[25\sqrt{3}\]sq.cm done clear
  View Solution play_arrow

• question_answer15)
  ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
  A)
   area \[\left( \Delta BCP \right)\] = area \[\left( \Delta DPQ \right)\] done clear
  B)
   area \[\left( \Delta BCP \right)\] > area \[\left( \Delta DPQ \right)\] done clear
  C)
   area \[\left( \Delta BCP \right)\] < area \[\left( \Delta DPQ \right)\] done clear
  D)
   area \[\left( \Delta BCP \right)\] + area \[\left( \Delta DPQ \right)\] = area \[(\Delta \,BCD)\] done clear
  View Solution play_arrow

• question_answer16)
  In \[\Delta \mathbf{PQR}\], the line drawn from the vertex P intersects QR at a point S. If QR = 4.5 cm and SR = 1.5 cm then the ratios of the area of triangle PQS and triangle PSR is
  A)
   4 : 1                             done clear
  B)
   3 : 1             done clear
  C)
   3 : 2                             done clear
  D)
   2 : 1 done clear
  View Solution play_arrow

• question_answer17)
  ABCD is a parallelogram X and Y are the mid points of sides BC and CD respectively. If the area of \[\Delta \,\mathbf{ABC}\] is 16\[\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\], then the area of \[\Delta \mathbf{AXY}\]is
  A)
   12 \[c{{m}^{2}}\] done clear
  B)
   8 \[c{{m}^{2}}\] done clear
  C)
   9 \[c{{m}^{2}}\]                                 done clear
  D)
   10 \[c{{m}^{2}}\] done clear
  View Solution play_arrow

• question_answer18)
  PQR is a right angles triangle Q being the right angle. Mid-points of QR and PR are respectively Q' and P? Area of \[\Delta \mathbf{P}'\mathbf{Q}'\mathbf{R}'\] is
  A)
   \[\frac{1}{2}\times area\text{ }of\text{ }\Delta PQR\]  done clear
  B)
   \[\frac{2}{3}\times area\text{ }of\text{ }\Delta PQR\] done clear
  C)
   \[\frac{1}{4}\times area\text{ }of\text{ }\Delta PQR\]  done clear
  D)
   \[\frac{1}{8}\times area\text{ }of\text{ }\Delta PQR\] done clear
  View Solution play_arrow

• question_answer19)
                                                                                                          From any point inside an equilateral triangle, the lengths of perpendiculars 015 the sides are 'a? cm ?b? cm and ?c? cms. Its area (in\[\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\]) is
  A)
   \[\frac{\sqrt{2}}{3}\left( a+b+c \right)\]              done clear
  B)
   \[\frac{\sqrt{3}}{3}{{\left( a+b+c \right)}^{2}}\] done clear
  C)
   \[\frac{\sqrt{3}}{3}\left( a+b+c \right)\]              done clear
  D)
   \[\frac{\sqrt{2}}{3}{{\left( a+b+c \right)}^{2}}\] done clear
  View Solution play_arrow

• question_answer20)
  ABCD is a square. Draw a triangle QBC on side BC considering BC as base and draw a triangle PAC on AC as its base such that \[\Delta QBC\sim PAC\]. Then,\[\frac{Area\,of\,\Delta QBC}{Area\,of\ \Delta PAC}\]is equal to
  A)
   \[\frac{1}{2}\]  done clear
  B)
   \[\frac{2}{1}\] done clear
  C)
   \[\frac{1}{3}\]                          done clear
  D)
   \[\frac{2}{3}\] done clear
  View Solution play_arrow

• question_answer21)
  A rectangular park 60 metre long and 40 metre wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 metre2 then the width of the road is
  A)
   3 metre    done clear
  B)
   5 metre done clear
  C)
   6 metre                         done clear
  D)
   2 metre done clear
  View Solution play_arrow

• question_answer22)

  Direction: Each of the questions Mow consists of a questions followed by statements. You have to study the questions and the statements and decide which of the statement (s) is/are necessary to answer the question?

  What is the area of rectangular field?

  (I) The perimeter of the field is 110 metres.

  (II) The length is 5 metres more than the width.

  (III) The ratio between length and width is 6:5 respectively.

  A)
   I and II only                       done clear
  B)
   Any two of the three done clear
  C)
   I, and either II or III only           done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer23)

  Direction: Each of the questions Mow consists of a questions followed by statements. You have to study the questions and the statements and decide which of the statement (s) is/are necessary to answer the question?

  A path runs around a rectangular lawn. What is the width of the path?

  (I) The length and breadth of the lawn are in the ratio of 2:1 respectively.

  (II) The width of the path is twenty times the length of the lawn.

  (III) The cost of gravelling the path @ Rs. 50 per nr is Rs. 4416.

  A)
   All I, II and III      done clear
  B)
   III, and either I or II done clear
  C)
   I and III only                 done clear
  D)
   II and III only done clear
  View Solution play_arrow

• question_answer24)
  The area of a rectangle lies between 40\[\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\] and 45\[\mathbf{c}{{\mathbf{m}}^{\mathbf{2}}}\]. If one of the sides is 5cm, then its diagonal lies between
  A)
   8 cm and 10 cm         done clear
  B)
   9 cm and 11 cm done clear
  C)
   10 cm and 12 cm          done clear
  D)
   11 cm and 13 cm done clear
  View Solution play_arrow

• question_answer25)
  ABCD is a parallelogram. E is a point BC such that BE : EC = m : n. If AE and BD intersect in F, then what is the ratio of the area of \[\Delta \mathbf{PEB}\] to the area of \[\Delta \mathbf{AFD}\]?
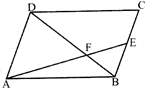
  A)
   \[m\text{/}n\]                            done clear
  B)
   \[{{\left( m\text{/}n \right)}^{2}}\] done clear
  C)
   \[{{\left( n\text{/}m \right)}^{2}}\]                                done clear
  D)
   \[{{\left[ m/{{(n+m)}^{2}} \right]}^{2}}\] done clear
  View Solution play_arrow

• question_answer26)
  ABCD is a trapezium with parallel sides AB = 2cm and DC = 3cm. E and F are the mid- points of the non-parallel sides. The ratio of area of ABFE to area of EFCD is
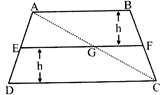
  A)
   9:10                             done clear
  B)
   8:9            done clear
  C)
   9:11      done clear
  D)
   11:9 done clear
  View Solution play_arrow

• question_answer27)
  Let LMNP be a parallelogram and NR be perpendicular to LP. If the area of the parallelogram is six times the area of \[\Delta \mathbf{RNP}\] and RP = 6 cm then LR is equal to
  A)
   15 cm                          done clear
  B)
   12cm   done clear
  C)
   9 cm                done clear
  D)
   8 cm done clear
  View Solution play_arrow

• question_answer28)
  In the given figure, ABCD is a quadrilateral with AB parallel to DC and AD parallel to BC, ADC is a right angle. If the perimeter of the\[\Delta \mathbf{ABE}\]is 6 units, what is the of the quadrilateral?
  A)
   \[2\sqrt{3}\]sq units   done clear
  B)
   4 sq units done clear
  C)
   3 sq units                    done clear
  D)
   \[4\sqrt{3}\]sq units done clear
  View Solution play_arrow

• question_answer29)
  In the figure given below, ABCD is a parallelogram. P is a point in BC such that PR : PC = 1 : 2, DP produced meets AB produced at Q, If the area of the \[\Delta BPQ\] is 20 Sq. units, what is the area of the\[\Delta DCP\]?
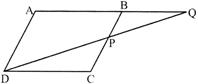
  A)
   20 sq units               done clear
  B)
   30 sq units done clear
  C)
   40 sq units                    done clear
  D)
  none of the above done clear
  View Solution play_arrow

• question_answer30)
  From a point within an equilateral triangle, perpendicular are drawn to its sides. The lengths of these perpendicular are 6 m, 7m and 8m. Find the area of the triangle
  A)
   160 sq. m                     done clear
  B)
   \[147\sqrt{3}\]sq. m done clear
  C)
   \[210\sqrt{3}\]sq. m.            done clear
  D)
   \[27\sqrt{3}\]sq. nz done clear
  View Solution play_arrow