-
question_answer1) In \[\Delta \,ABC,D\]and \[E\] are points \[AC\] and \[BC\] respectively such that \[DE\parallel AB\]. If \[AD=2x,\text{ }BE=2x-1,CD=x+1\] and\[CE=x-1\], then find the value of \[x\].
View Answer play_arrow
-
question_answer2) In A, B and C are interior angles of \[\Delta \text{ }ABC\], then prove that: \[\sin \frac{(A+C)}{2}=\cos \frac{B}{2}\].
View Answer play_arrow
-
question_answer3) If \[x=3\text{ }sin\text{ }\theta \] and \[y=4\text{ }cos\,\theta \], find the value of \[\sqrt{16{{x}^{2}}+9{{y}^{2}}}\].
View Answer play_arrow
-
question_answer4) If empirical relationship between mean, median and mode is expressed as mean \[=k\](3 median\[\]mode), then find the value of\[k\].
View Answer play_arrow
-
question_answer5) Express 23150 as product of its prime factors. Is it unique?
View Answer play_arrow
-
question_answer6) State whether the real number 52.0521 is rational or not. If it is rational express it in the form \[\frac{p}{q}\], where \[p,q\] are co-prime, integers and \[q\ne 0\]. What can you say about prime factorisation of \[q\]?
View Answer play_arrow
-
question_answer7)
| Given the linear equation \[x-2y-6=0\], write another linear equation in these two variables, such that the geometrical representation of the pair so formed is: |
| (i) coincident lines |
| (ii) intersection lines |
View Answer play_arrow
-
question_answer8) In an isosceles \[\Delta \text{ }ABC\] right angled at B, prove that \[A{{C}^{2}}=2A{{B}^{2}}\].
View Answer play_arrow
-
question_answer9)
| Prove the following identity: |
| \[{{\left[ \frac{1-\tan \,A}{1-\cot \,A} \right]}^{2}}={{\tan }^{2}}A:\angle A\] is acute |
View Answer play_arrow
-
question_answer10)
| Given below is a cumulative frequency distribution table. Corresponding to it, make an ordinary frequency distribution table. |
| \[x\] | \[cf\] |
| More than or equal to 0 | 45 |
| More than or equal to 10 | 38 |
| More than or equal to 20 | 29 |
| More than or equal to 30 | 17 |
| More than or equal to 40 | 11 |
| More than or equal to 50 | 6 |
View Answer play_arrow
-
question_answer11) Find LCM and HCF of 3930 and 1800 by prime factorisation method.
View Answer play_arrow
-
question_answer12) Using division algorithm, find the quotient and remainder on dividing \[f(x)\] by \[g(x)\] where \[f(x)=6{{x}^{3}}+13{{x}^{2}}+x-2\] and\[g(x)=2x+1\].
View Answer play_arrow
-
question_answer13) If three zeroes of a polynomial \[{{x}^{4}}-{{x}^{3}}-3{{x}^{2}}+3x\] are \[0,\sqrt{3}\] and \[-\sqrt{3}\], then find the fourth zero.
View Answer play_arrow
-
question_answer14)
| Solve the following pair of equations by reducing them to a pair of linear equations: |
| \[\frac{1}{x}-\frac{4}{y}=2\] |
| \[\frac{1}{x}+\frac{3}{y}=9\] |
View Answer play_arrow
-
question_answer15) \[\Delta \text{ }ABC\] is a right angled triangle in which \[\angle B=90{}^\circ \]. D and E are any point on AB and BC respectively. Prove that\[A{{E}^{2}}+C{{D}^{2}}=A{{C}^{2}}+D{{E}^{2}}\].
View Answer play_arrow
-
question_answer16)
| In the given figure, RQ and TP are perpendicular to PQ, also \[TS\bot PR\] prove that \[\text{ST}\text{.RQ=PS}\text{.PQ}\]. |
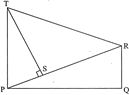 |
View Answer play_arrow
-
question_answer17) If sec\[A=\frac{2}{\sqrt{3}}\], find the value of \[\frac{\tan \,\,A}{\cos \,\,A}+\frac{1+\sin \,\,A}{\tan \,\,A}\]
View Answer play_arrow
-
question_answer18) Prove that: \[{{\sec }^{2}}\theta -{{\cot }^{2}}(90{}^\circ -\theta )=co{{s}^{2}}(90{}^\circ -\theta )+co{{s}^{2}}\theta .\]
View Answer play_arrow
-
question_answer19)
| For the month of February, a class teacher of Class IX has the following absentee record for 45 students- Find the mean number of days, a student was absent. |
| Number of days of absent | 0 ? 4 | 4 ? 8 | 8 ? 12 | 12 ? 16 | 16 ? 20 | 20 ? 24 |
| Number of students | 18 | 3 | 6 | 2 | 0 | 1 |
View Answer play_arrow
-
question_answer20)
| Find the missing frequency (x) of the following distribution, if mode is 34.5: |
| Marks obtained | 0 ? 10 | 10 ? 20 | 20 ? 30 | 30 ? 40 | 40 ? 50 |
| Number of students | 4 | 8 | 10 | x | 8 |
View Answer play_arrow
-
question_answer21) Prove that \[\sqrt{5}\] is an irrational number. Hence show that \[3+2\sqrt{5}\] is also an irrational number.
View Answer play_arrow
-
question_answer22) Obtain all other zeroes or the polynomial\[{{x}^{4}}+6{{x}^{3}}+{{x}^{2}}-24x-20\], if two of its zeroes are \[+2\] and \[-5\].
View Answer play_arrow
-
question_answer23)
| Draw graph of following pair of linear equations: |
| \[y=2(x-1)\] |
| \[4x+y=4\] |
| Also write the coordinate of the points where these lines meets x-axis and y-axis. |
View Answer play_arrow
-
question_answer24) A boat goes \[30\text{ }km\] upstream and \[44\text{ }km\] downstream in 10 hours. The same boat goes \[40\text{ }km\] upstream information some student guessed the speed of the boat in still water as \[8.5\text{ }km/h\] and speed of the stream as \[3.8\text{ }km/h\]. Do you agree with their guess? Explain what do we learn from the incident?
View Answer play_arrow
-
question_answer25) In an equilateral \[\Delta \text{ }ABC,\text{ }E\] is any point on \[BC\] such that \[BE=\frac{1}{4}BC\]. Prove that \[16\text{ }A{{E}^{2}}=13\text{ }A{{B}^{2}}\].
View Answer play_arrow
-
question_answer26)
| In the figure if \[\angle ABD=\angle XYD=\angle CDB=90{}^\circ .\text{ }AB=a,XY=c\] and \[CD=b\], then prove that\[c\text{ (}a+b)=ab\]. |
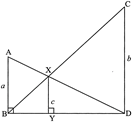 |
View Answer play_arrow
-
question_answer27)
| In the \[\Delta \,ABC\](see figure), \[\angle A=\] right angle, \[AB=\sqrt{x}\] and \[BC=\sqrt{x+5}\]. Evaluate |
| \[sin\text{ }C.\text{ }cos\text{ }C.\text{ }tan\text{ }C+co{{s}^{2}}C.\text{ }sin\text{ }A\] |
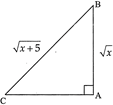 |
View Answer play_arrow
-
question_answer28) If \[\frac{\cos \,B}{\sin \,A}=n\] and \[\frac{\cos \,B}{\cos \,A}=m\] then show that \[({{m}^{2}}+{{n}^{2}})co{{s}^{2}}A={{n}^{2}}\].
View Answer play_arrow
-
question_answer29) Prove that: \[\frac{\sec \,A-1}{\sec \,A+1}={{\left( \frac{\sin \,A}{1+\cos \,A} \right)}^{2}}={{(cot\,A-cosec\,A)}^{2}}\]
View Answer play_arrow
-
question_answer30)
| Following table shows marks (out of 100) of students in a class test: |
| Marks | No. of students |
| More than or equal to 0 | 80 |
| More than or equal to 10 | 77 |
| More than or equal to 20 | 72 |
| More than or equal to 30 | 65 |
| More than or equal to 40 | 55 |
| More than or equal to 50 | 43 |
| More than or equal to 60 | 28 |
| More than or equal to 70 | 16 |
| More than or equal to 80 | 10 |
| More than or equal to 90 | 8 |
| More than or equal to 100 | 0 |
| Draw a ?more than type? ogive. From the curve, find the median. Also, check the value of the median by actual calculation. |
View Answer play_arrow
-
question_answer31)
| From the following data find the median age of 100 residents of a colony who took part in swachch bharat abhiyan: |
| Age (in yrs.) More than or equal to | No. of residents |
| 0 | 50 |
| 10 | 46 |
| 20 | 40 |
| 30 | 20 |
| 40 | 10 |
| 50 | 3 |
View Answer play_arrow



