Area and Perimeter
Category : 5th Class
LEARNING OBJECTIVE
This lesson -will help you to:—
Real – Life Example
Historical preview
QUICK CONCEPT REVIEW
AREA is the space occupied by a closed figure. For example: the area covered by a carpet on the floor.
PERIMETER is the distance around a closed figure. For I example: when you take a round around your play ground the distance covered by you in taking one round is called the perimeter.
Area of square
As we know that the square has all its four sides equal. The formula for area of a square is side x side.
For example: Calculate the area of a square with each side of 5 cm.
Then to calculate the area of the square we apply the formula side x side.
\[5\times 5=25,\] so the area of the square will be 25.
UNITS: While calculating the area of square we are multiplying two numbers with same unit. Like in the example above, 5cm is multiplied by 5cm so the result will be in \[c{{m}^{2}}.\] This means the area will be 25\[c{{m}^{2}}.\]Whenever we find area of the square the units will be square units, like m2, \[c{{m}^{2}}.\] or \[inc{{h}^{2}}.\] etc.
Amazing Facts
For example, if there are three rectangles with sides:
In all of the above given rectangles, perimeter is same. The rectangle in which the difference between the sides is least (case iii), that rectangle has the greatest area.
[Difference in sides – (i) 5 – 1 = 4, (ii) 4 – 2 = 2, (iii) 3 – 3]
Perimeter of square
When we find the perimeter of square we add all the sides or we multiply the length of one side by 4.
For example: Calculate the perimeter of a square with each side 4 units.
Perimeter of square = \[4\times side\]
So, \[4\times 4=16\Rightarrow \] the perimeter of square is 16 units.
The units of perimeter of a figure will be the same as that of units of side of the figure. Like cm, m and inches.
Area of rectangle
As we know there is length and breadth in a rectangle.
So, to calculate area of rectangle we multiply length by breadth.
So area of a rectangle is length \[\times \] breadth
For example to calculate the area of a rectangle with length = 5cm and breadth = 9cm, we multiply 5 by 9
\[5\times 9=45,\]So the area of rectangle is \[45c{{m}^{2}}.\]
Perimeter of rectangle
If we want to calculate the distance around a rectangle we shall have both length and breadth twice. So to calculate the perimeter of a rectangle we add all the four sides.
\[\Rightarrow \]Perimeter of rectangle = I + b + I + b where I = length and b = breadth
= 21 + 2b
=2(l + b)
So, the perimeter of rectangle = 2(1 + b)
Triangle
Area of triangle \[=\frac{1}{2}\times base\times height.\]
Height: In a triangle, the length of the perpendicular which is drawn from vertex to the opposite side is called height of the triangle.
Base: In a triangle, the length of the side of the triangle on which perpendicular is drawn is called base.
Perimeter of a triangle is sum of lengths of three sides.
Units
Area —sq. units —— \[c{{m}^{2}},{{m}^{2}}\] etc.
Perimeter -—single units —cm, m etc.
Holding capacity of a container is called volume.
\[=length\times breadth\times heigth\]
![]()
Point to remember
We can also calculate the length of sides if perimeter of area is given.
Say we know the area of rectangle and its length, then to calculate breadth:
\[Area=length\times breadth\]
\[\Rightarrow \] \[Area/length=breadth\]
Similarly we can find the other missing dimensions.
\[=side\times side\times side\]
Circumference of a circle
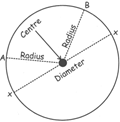
The perimeter of a circle is called the circumference. The distance between the centre and any point on the circle is called its radius. And the line segment passing through the centre of the circle, whose end points lie on the circle is called the diameter of the circle. The diameter of a circle is twice the radius.
Finding circumference
To find the circumference of a circle we must remember Circumference \[\frac{\text{Circumference}}{\text{diameter}}\text{=3}\text{.14or}\frac{\text{22}}{\text{7}}\text{.}\]
This makes it much easier to find the circumference of a circle. Measure the diameter of the circle and multiply it by 3.14 or \[\frac{\text{22}}{\text{7}}\] to get the circumference.
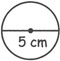
For eg. The diameter of a circle is 5cm. Find the circumference.
Circumference = \[5\times 3.14cm=15.7cm\]
You need to login to perform this action.
You will be redirected in
3 sec
