5th Class Mathematics Area, Perimeter and Volume Area

  Area

All the geometrical shapes occupies some space. The occupied space by a geometrical shape is called area of that geometrical shape.

Shaded part in the above figures represent area.  

  Area of a Triangle

Area of a triangle \[=\frac{1}{2}\times \] base x height.

Height

In a triangle, the length of the perpendicular which is drawn from vertex to the opposite side is called height of the triangle.

Base 

In a triangle, the length of the side of the triangle on which perpendicular is drown is called base.

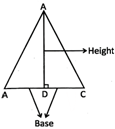
Area of a triangle \[=\frac{1}{2}\times \] base \[\times \] height

In triangle ABC

Height = CD and base = AB

Area of the triangle \[ABC=\times AB\times CD.\]  

Find the area of the following figure:

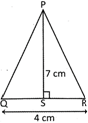
Explanation

Area of a triangle \[=\frac{1}{2}\times \] base \[\times \]height

In triangle PQR

Area of the triangle \[\text{PQR=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ QR }\!\!\times\!\!\text{ PS=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ 4cm }\!\!\times\!\!\text{ 7cm14c}{{\text{m}}^{\text{2}}}\]  

Area of a Rectangle

Area of a rectangle = length \[\times \] breadth.  

Length

The longer side of a rectangle is called length of the rectangle.  

  Breadth

The shorter side of a rectangle is called breadth of the rectangle.

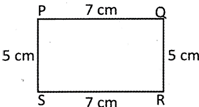
In the rectangle PQRS

Length of rectangle = Longer side PQ = RS = 7 cm

Breadth of the rectangle = Shorter side

QR = SP = 5 cm

Area of the rectangle PQRS = Length \[\times \] Breadth

= PQ \[\times \] QR.  

Find the area of the following figure:

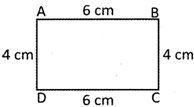
In rectangle ABCD

Length = AB = 6 cm

Breadth = BC = 4 cm

Thus area of the rectangle 3 \[\text{ABCD=AB }\!\!\times\!\!\text{ BC=6 cm }\!\!\times\!\!\text{ 4 cm=24 c}{{\text{m}}^{\text{2}}}\text{.}\]  

Area of a Square

Area of a square\[~=\text{ }sid{{e}^{2}}.\]

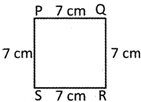
In the square PQRS PQ=QR=RS=SP Area of the square \[PQRS\text{ }=\text{ }PQ\text{ }\times \text{ }PQ\] \[=P{{Q}^{2}}.\]

Find the area of the following figure:

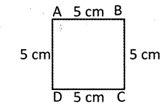
In square ABCD

AB = BC = CD = DA = 5 cm

Area of the square \[\text{ABCD }=\text{ A}{{\text{B}}^{\text{2}}}\]

\[{{(5cm)}^{2}}=25c{{m}^{2}}\]  

Area of a Circle

Area of the circle \[=\pi {{r}^{2}}\]

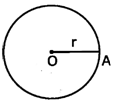
To find the area of a circle, square of the radius is multiplied by the constant \[\pi .\]  

Find the area of the circle whose radius is 11.9 cm.

Solution:

Area of a circle \[\pi {{r}^{2}}\]

\[=\frac{22}{7}\times 11.9\text{ }cm\text{ }\times 11.9\text{ }cm\]

\[=445.06\text{ }c{{m}^{2}}\]