5th Class Mathematics Decimals Decimals

LEARNING OBJECTIVES

This lesson will help you to:

• understand the expanded form of a decimal number.
• learn the conversion of decimal into fraction & vice-versa.
• identify the different types of decimals.
• compare decimals.
• learn about the different operations on the decimal numbers.

Real – Life Example

• Decimals are used in expressing money, distance and length, weight and capacity.
• Decimals are frequently used in Science from laboratory experimental data.
• Decimals are used when adding and counting money. Whenever we have some number of paise that do not add up to a complete rupee, we express the amount as a decimal.
• Decimals are used in all types of measurements. Eg: When you fall sick, doctor prescribes you medicine as 2.5 ml twice a day or so on.

QUICK CONCEPT REVIEW

(i) Decimal number is another way of representing   fractions.

• Decimal is a fraction having the denominator power of 10.
• Decimal part read as separately one by one like 25.921 is read as twenty five point nine, two, one.
• Decimal numbers have a whole part and a decimal part separated by a decimal point.

Amazing Facts

• One decimal place to the right of the demical point is he ‘’tenths’’ place, but one decimal place to the left ‘’ones’’ place. The ‘’tens’’ place is two places to the left.
• Decimal notation is the writing of numbers in a base-10 numeral system.
• The word decimal is derived from the Latin root decem (ten).

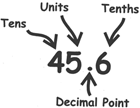
(ii)         The decimal point goes between units and tenths place.

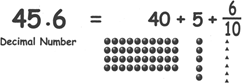
Place of a decimal: In a decimal number, position or "place" of each digit is important.

In the number 237,

• the "7" is in the Units position, meaning just 7
• the "3" is in the Tens position meaning 3 tens

and the "2" is in the Hundreds position, meaning  2 hundreds.      

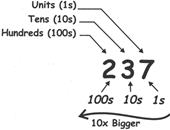
"Two Hundred Thirty Seven"      

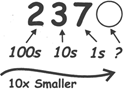
(iv)         As we move left, each position is 10 times bigger,

Hundreds are 10 times bigger than Tens.         

• As we move right, each position is 10 times" smaller From Hundreds, to Tens, to Units

Expanded form of decimals

\[315.162=300+10+5+\frac{1}{10}+\frac{6}{100}+\frac{2}{1000}\]

(vi)         Like and unlike decimals: Like decimals hove same decimal places unlike decimals have different decimal places.

                              Historical preview

• Decimal fractions were first developed and used by the Chinese in the 1 st century BC, and then spread to the Middle East and from there to Europe.
• The Jewish mathematician Immanuel Bonfils invented decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them.

Example: 2.56, 5.48, 0.25 etc., are like decimals and 0.2, 1.23, 2.236 etc., are unlike decimals.

(vii)        Equivalent decimals; the decimals which have same value are called equivalent decimals.

(viii)       Decimals on a number line: Each decimal number can be plotted on the number line using units, tenths, hundredths etc.

(ix)         Decimal fractions: A decimal number can also be represented as fraction.

A decimal fraction is a fraction where the .denominator is a number such as (10, 100, 1000 etc).

i.e. a power of tens.

Following decimal number have following fraction

\[2.3=\frac{23}{10},13.76=\frac{1376}{100}.\]

Conversion of a Decimal into a Fraction

Step 1: Remove the point from the decimal and write the obtained number as the numerator.

Step 2: Write 1 as denominator and put zeroes right to it so that the number of zeroes is equal to the number of digits right to the point in the given decimal.

Example:   \[23.56=\frac{2356}{100}.\]

Comparing two decimal numbers

• We can compare two like decimals just as we compare two whole numbers ignoring the decimal point.
• For comparing two unlike decimals, first convert them into like decimals then compare.

Addition of Decimals

Step 1: Convert the given decimals into like decimals.

Step 2: Write the addends one under the other so that the decimal points of all the addends are in the same column.

Step 3: Add as in the case of whole numbers.

Step 4: In the sum, put decimal point directly under the decimal points in the addends.

Subtraction of Decimals

Step 1: Convert the given decimals into like decimals.

Step 2: Write the smaller number under the larger one so that their decimal points are in the same column.

Misconcept /Concept

Misconcept:  Longer is larger misconcept:  A longer decimal may not be a larger number than a shorter decimal

Concept:  Shorter is larger misconcept:   A Shorter decimal is a   larger number than a longer decimal.     

Step 3: Subtract as in the case of whole numbers.

Step 4: In the difference, put the decimal point directly under the decimal points of the given numbers.

Multiplication of a Decimal by a Whole Number

Step 1: Multiply the decimal without the decimal point by the whole number.

Step 2: Place the decimal point so as to obtain as many decimal places in the product as there are in the decimal.                                             

Multiplication of Two Decimals                

Step 1: Multiply the two decimals without the decimal points, just like whole numbers.                       

Step 2: In the product, place the decimal point so that the number of decimal places in the product is equal to the sum of the decimal places in the given decimals.    

Division of a Decimal by a Whole Number      

Step 1: Perform the division by considering the dividend a whole number.

Step 2: When the whole number part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.

Division of a Decimal by a Decimal

Step 1: Convert the divisor into a whole number by multiplying the dividend and the divisor by 10, 100 or 1000 etc. depending upon the number of decimal places in the divisor.

Step 2: Now, divide the new dividend by the whole number as discussed above.

ROUNDING DECIMAL

Rounding means reducing the digits in a number while trying to keep its value similar.

Example: 73 rounded to the nearest ten is 70, because 73 is closer to 70 than to 80.

Rules to Round Numbers

• Decide which is the last digit to keep.
• Leave it the same if the next digit is less than 5 (this is called rounding down).
• But increase it by 1 if the next digit is 5 or more (this is called rounding up).

Rounding Decimal

Rounding Whole Numbers

Rounding to Significant Digits

PLAY TIME

Divide the students in two teams. Assign the numbers (0 – 9) to both the teams. Ask two teams to make the largest and smallest decimal numbers with one decimal place and two decimal places with 1, 2, 3 digits as whole number part. The team who makes the maximum correct number wins the game.

USES OF DECIMAL SYSTEM

We have seen that 100 cm = 1 m

1000 m=1 km, 1000 ml= \[1\ell \]. 1000 g = 1 kg etc.

In money also, we use the conversion 100 paise = 1 rupee.

We can use the decimal system in all these places to convert a smaller unit to a bigger unit.