Lines & Angles
Category : 7th Class
LINES AND ANGLES
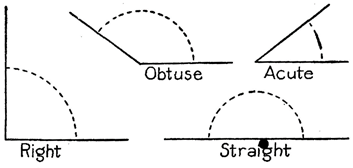
FUNDAMENTALS
![]()
![]()
![]()
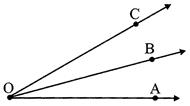
(Here 'O' is the starting point for ray OA)
The symbol of angle is\[\angle \]. An angle is measured in degrees\[({}^\circ )\].
The angle formed by the two rays \[\overline{AB}\] and \[\overline{AC}\] is denoted by \[\angle BAC\] or\[\angle CAB\].
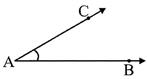
The two rays \[\overline{AB}\] and \[\overline{AC}\] are called the arms and the common initial point 'A' is called the vertex of the angel ABC.
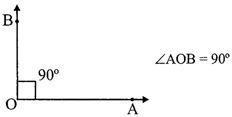
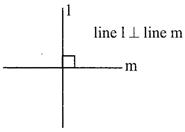
I. Right angle: An angle whose measure is equal to \[90{}^\circ \]is called a right angle.
II. Acute angle: An angle whose measure is less than \[90{}^\circ \]is called an acute angle.

III. Obtuse angle: Angle whose measure is greater than \[90{}^\circ \]but less than \[180{}^\circ \]is called an obtuse angle.
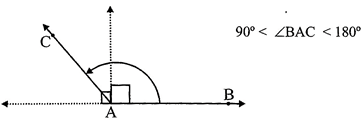
IV. Reflex angle: An angle which is greater than \[180{}^\circ \]but less than \[360{}^\circ \]is calleda reflex angle.
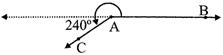
\[180<\angle BAC<360{}^\circ \]
V. Zero angle: An angle whose measure is \[0{}^\circ \]is called a zero angle.
Note: In a zero angle, the rays \[\overline{OA}\] and \[\overline{OB}\] coincide without any rotation of \[\overline{OB}\] . That is no angle is FORMED between the two rays.
![]()
VI. Straight angle: An angle whose measure is equal to \[180{}^\circ ,\]is called a straight angle.
![]()
VII. Complete angle: An angle whose measure is exactly equal to \[360{}^\circ \]is called a complete angle.

Intersecting lines and vertically opposite angles: If two distinct lines have a common point of intersection, they are called intersecting lines. In the in the figure below, lines AB and CD (distinct lines) intersect at point '0'. Now, the two angle......
I. Vertically opposite angles: Two angles having the same vertex are said to form a pair of vertically opposite angles. Vertically opposite angles are formed when two lines intersect.
In the figure given, \[\angle AOD\] and \[\angle BOC\] are a pair of vertically opposite angles because they have common vertex at O and also OB, OA; OC, OD are two pairs of opposite rays.
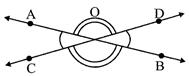
Similarly, we find that \[\angle BOD\] and \[\angle AOC\] is another pair of vertically opposite angles.
II. Complementary angles: Two angles are said to be complementary if the sum of their measures is equal to \[90{}^\circ .\]
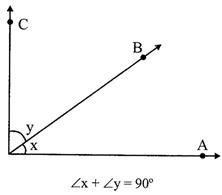
Here \[\angle x+\angle y=90{}^\circ ,\]therefore \[\angle x\] and \[\angle y\]are complementary angles.
III. Supplementary angles: Two angles are said to be supplementary if the sum of their measures is equal to \[180{}^\circ .\]
Here, \[\angle x+\angle y=180{}^\circ ,\]therefore \[\angle x\] and \[\angle y\] are supplementary angles.
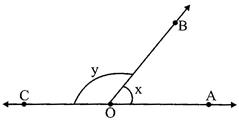
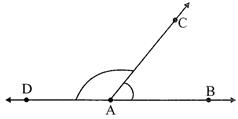
IV. Adjacent angles: Angles having a common vertex, a common arm and the non- common arms lying on either side of the common arm are called adjacent angles.
In the given figure, \[\angle AOB\] and \[\angle BOC\] have a common vertex '0', a common arm OB and non - common arms, \[\overline{OA}\] and \[\overline{OC}\] are on opposite sides of \[\overline{OB}\], so these are adjacent angles. Also, by the same logic, complementary angle are adjacent angle. Similarly, pair of supplementary angle are adjacent.
V. Linear pair of angles: Two adjacent angles make a linear pair of angles, if the non- common arms of these angle form two opposite rays (with same end point).
In the figure given, the \[\angle BAC\] and \[\angle DAC\] form a linear pair of angles because the non-common arms AB and AD of the two angles are the opposite rays, with the same vertex A.
Moreover, \[\angle BAC+\angle DAC=180{}^\circ \]
Note:
1. A linear pair is always supplementary.
2. A linear pair of angles is always adjacent while a pair of adjacent angles need not be a linear pair.
PAIR OF LINES
![]()
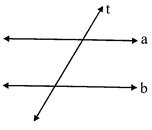
In the above figure 't' is a transversal to the lines a and b.
In the figure given below, lines a and b are cut by the transversal ?t?. The eight angles marked 1 to 8 are shown as follows:
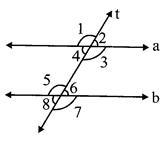
Table: 8.1
|
Angle type |
Angle name |
Remarks |
|
Interior angle |
\[\angle 3,\angle 4,\angle 5,\angle 6\] |
|
|
Exterior angle |
\[\angle 1,\angle 2,\angle 7,\angle 8\] |
|
|
Corresponding angles |
\[\angle 1\] and \[\angle 5,\]\[\angle 2\]and \[\angle 6,\] \[\angle 4\] and \[\angle 8\], \[\angle 3\] and \[\angle 7\] |
Corr. angles are equal |
|
Alternate interior angle |
\[\angle 3\] and \[\angle 5,\angle 4\] and \[\angle 6\] |
Alternate angle are equal |
|
Alternate exterior angle |
\[\angle 1\] and \[\angle 7,\angle 2\] and \[\angle 8\] |
Alternate angle are equal |
|
Interior angles on the same side of the transversal |
\[\angle 4\] and \[\angle 5,\angle 3\] and \[\angle 6\] |
Their sum = \[180{}^\circ \] |
Note: (i) The F-Shape stands for Corresponding angles.
(ii) The Z- shape stands for alternate angle.
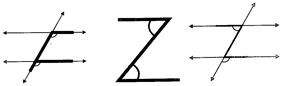
(a) Corresponding angels are equal.
(b) Alternate interior angle are equal.
(c) Interior angles on the same side of the transversal are supplementary.
In the above figure, let us draw one more transversal, \[{{t}_{2}}\] parallel to transversal\[{{t}_{1}}\].
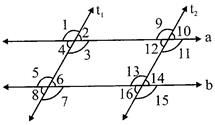
Now, if we mentally rotate the whole figure clockwise by \[90{}^\circ \] then \[{{t}_{1}}//{{t}_{2}}\]and parallel lines 'a' and 'b' are transversal. So, we can write, Interior angles \[=\angle 2,\text{ }\angle 3,\text{ }\angle 9,\text{ }\angle 12\] (considering 'a' as transversal) on \[{{t}_{1}}\] & \[{{t}_{2}}\]
Exterior angles \[\angle 1,\angle 4,\angle 10,\angle 11\] (considering 'a' as transversal) on \[{{t}_{1}}\] & \[{{t}_{2}}\]
Elementary question for genius students
Q.1: Construct as table like table \[8.1\] for the above case where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parallel and line 'a' is transversal to\[{{t}_{1}}\]&\[{{t}_{2}}\].
Q.2: Similarly construct a table with parallel lines with \[{{t}_{1}}\] & \[{{t}_{2}},\] and both lines 'a' and 'b' are transversals.
You need to login to perform this action.
You will be redirected in
3 sec
