9th Class Mathematics Surface Areas and Volumes Surface Area and Volume

Surface Area and Volume

In this chapter, we will learn about some important formulas related to \[2-D\] and \[3-D\] geometrical shapes.

Area of a Triangle

• Area of a triangle \[=\frac{1}{2}\times \] (Perpendicular) \[\times \] Base
• Area of a triangle having lengths of the sides a, b and c is

\[=\sqrt{s(s-a)(s-b)(s-c)}\] sq. units,

Where \[s=\frac{1}{2}\] (a + b + c)

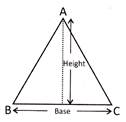
• Area of an equilateral triangle \[=\frac{\sqrt{3}}{4}{{a}^{2}}\], where a is the side of the equilateral triangle.

Circle

• Circumference of the circle = \[2\pi r\]
• Area of the circle = \[\pi {{r}^{2}}\]
• Area of the semicircle = \[\frac{1}{2}\pi {{r}^{2}}\]
• Perimeter of the semicircle =\[\pi r+2r\]

Length of Arc and Area of a Sector

Let an arc AB makes an angle \[\theta <180{}^\circ \] at the center (O) of a circle of radius r, then we have:

• Length of the arc AB = \[\frac{2\pi r\theta }{360{}^\circ }\]
• Area of the sector OACB = \[\frac{\pi {{r}^{2}}\theta }{360{}^\circ }\]

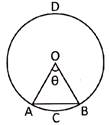
• Area of the minor segments ACBA = area of sector OACB\[~-\]area of the corresponding triangle AOB
• Area of the major segment ADBA = area of the circle \[~-\] area of the minor segment

Perimeter and Area of a Rectangle

Let ABCD be a rectangle in which length AB = l units, breadth BC = b units then we have:

• Area = (\[l\times b\]) square units
• Length (l) \[=\frac{area\,\,(A)}{breadth\,\,(B)}\] units

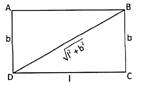
• breadth (b) \[=\frac{area\,\,(A)}{length\,\,(l)}\] units
• Diagonal (d) = \[\sqrt{{{l}^{2}}+{{b}^{2}}}\]units

• Perimeter (p) = 2(l + b) units

Area of Four Walls of a Room

Let l, b and h are respectively the length, breadth and height of a room, then area of four walls of the room

\[=\text{ }\left\{ 2\text{ }\left( \text{l }+\text{ }b \right)\text{ }x\text{ }h \right\}\] sq units.

Perimeter and Area of Square

Let ABCD be a square with each side equal to ‘a’ units, then

• Area = \[{{a}^{2}}\] sq. units
• Area = \[\left( \frac{1}{2}\times {{(Diagonal)}^{2}} \right)\] sq. units

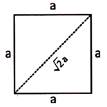
• Diagonal = \[a\sqrt{2}\] units
• Perimeter =4a units

Area of Some Special Types of Quadrilateral

• Area of a parallelogram = (base \[\times \] height)

• Area of a rhombus = \[\frac{1}{2}\times \] (product of diagonals)

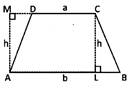
• Area of a Trapezium = \[\frac{1}{2}\] (Sum of lengths of parallel sides) \[\times \] (distance between them)

= \[\frac{1}{2}\] (a + b) \[\times \]h

Solids

The objects having definite shape and size are called solids. A solid occupies a definite space.

Cuboid

For a cuboid of length = l, breadth = b and height = h, we have:

• Volume = (l \[\times \] b \[\times \] h) cubic units
• Total surface area = 2 \[(lb+bh+lh)\] sq. units
• Lateral surface area = \[[2(l+b)\times h]\] sq. units
• Diagonal of a cuboid = \[\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}\]

Cube

For a cube having each edge = a units, we have:

• Volume = \[{{a}^{3}}\] cubic units
• Total surface area = \[6{{a}^{2}}\] sq. units
• Lateral surface area = \[4{{a}^{2}}\] sq. units
• Diagonal of a cube = a\[\sqrt{3}\]

Cylinder

Solids like jar, circular pencils, circular pipes, road rollers, gas cylinders are of cylindrical shape. For a cylinder of base radius = r units and height = h units, we have:

• Volume = \[\pi {{r}^{2}}h\] cubic units
• Curved surface area = \[2\pi rh\] square units
• Total surface area =

\[(2\pi rh+2\pi {{r}^{2}})=2\pi r(h+r)\] sq. units

Cone

Consider a cone in which base radius = r, height = h and slant height (l) =\[\sqrt{{{h}^{2}}+{{r}^{2}}}\], then we have:

• Volume of the cone = \[\frac{1}{3}\pi {{r}^{2h}}\]
• Curved surface area of the cone =\[\pi rl\]
• Total surface area of the cone = (curved surface area) + (area of the base) = \[\pi rl\]+\[\pi r{{l}^{2}}\]=\[\pi rl\]

(l + r)

Sphere

Objects like a football, a cricket ball, etc. are of spherical shapes. For a sphere of radius r, we have:

• Volume of the sphere =\[\frac{4}{3}\pi {{r}^{3}}\]
• Surface area of the sphere = \[4\pi {{r}^{2}}\]

Hemisphere

A plane through the centre of a sphere cuts it into two equal parts, each part is called a hemisphere. For a hemisphere of radius r, we have:

• Volume of the hemisphere = \[\frac{2}{3}\pi {{r}^{3}}\]
• Curved surface area of the hemisphere = \[2\pi {{r}^{2}}\]
• Total surface area of the hemisphere = \[3\pi {{r}^{2}}\]