-
question_answer1)
| DIRECTION: Read the passage given below and answer the questions that follows: |
| A brass ball of mass 100g is heated to \[100{}^\circ C\] and then dropped into 200g of turpentine in a calorimeter at \[15{}^\circ C\] The final temperature is found to be \[(\rho )\]. Take specific heat of brass as \[T=k\sqrt{\rho {{r}^{3}}/S}\] and water equivalent of calorimeter as 4g. |
The specific heat of turpentine is
A)
\[0.42\text{ }cal/g{}^\circ c\] done
clear
B)
\[0.96\text{ }cal/g{}^\circ c\] done
clear
C)
\[0.72\text{ }cal/g{}^\circ c\] done
clear
D)
\[0.12\text{ }cal/g{}^\circ c\] done
clear
View Solution play_arrow
-
question_answer2)
| DIRECTION: Read the passage given below and answer the questions that follows: |
| A brass ball of mass 100g is heated to \[100{}^\circ C\] and then dropped into 200g of turpentine in a calorimeter at \[15{}^\circ C\] The final temperature is found to be \[(\rho )\]. Take specific heat of brass as \[T=k\sqrt{\rho {{r}^{3}}/S}\] and water equivalent of calorimeter as 4g. |
Heat lost by the ball is approximately
A)
810 cal done
clear
B)
610 cal done
clear
C)
710 cal done
clear
D)
510 cal done
clear
View Solution play_arrow
-
question_answer3)
| DIRECTION: Read the passage given below and answer the questions that follows: |
| A brass ball of mass 100g is heated to \[100{}^\circ C\] and then dropped into 200g of turpentine in a calorimeter at \[15{}^\circ C\] The final temperature is found to be \[(\rho )\]. Take specific heat of brass as \[T=k\sqrt{\rho {{r}^{3}}/S}\] and water equivalent of calorimeter as 4g. |
Heat gained by turpentine and calorimeter is approximately
A)
810 cal done
clear
B)
610 cal done
clear
C)
710 cal done
clear
D)
510 cal done
clear
View Solution play_arrow
-
question_answer4)
At \[15{}^\circ C,\] a wheel has diameter of 30 cm and inside diameter of a steel rim is 29.9 cm. Coefficient of thermal expansion of steel is \[1.2\times {{10}^{-5}}{{/}^{o}}C\]. To what temperature, the rim must be heated so that it can slip over wheel?
A)
\[2787{}^\circ C\] done
clear
B)
\[2772{}^\circ C\] done
clear
C)
\[2529{}^\circ C\] done
clear
D)
\[2802{}^\circ C\] done
clear
View Solution play_arrow
-
question_answer5)
A beaker contains 200 gm of water. The heat capacity of the beaker is equal to that of 20 gm of water. The initial temperature of water in the beaker is\[20{}^\circ C\]. If 40 gm of hot water at \[92{}^\circ C\] is poured in it, the final temperature (neglecting radiation loss) will be nearest to
A)
\[58{}^\circ C\] done
clear
B)
\[68{}^\circ C\] done
clear
C)
\[73{}^\circ C\] done
clear
D)
\[78{}^\circ C\] done
clear
View Solution play_arrow
-
question_answer6)
The coefficient of apparent expansion of mercury in a glass vessel is \[153\times {{10}^{-6}}/{}^\circ C\] and in a steel vessel is \[144\times {{10}^{-6}}/{}^\circ C\]. If \[\alpha \] for steel is \[12\times {{10}^{-6}}/{}^\circ C,\] then that of glass is
A)
\[9\times {{10}^{-6}}/{}^\circ C\] done
clear
B)
\[6\times {{10}^{-6}}/{}^\circ C\] done
clear
C)
\[36\times {{10}^{-6}}/{}^\circ C\] done
clear
D)
\[27\times {{10}^{-6}}/{}^\circ C\] done
clear
View Solution play_arrow
-
question_answer7)
A solid object of mass M is made of material of specific heat capacity c, latent heat of fusion L and of very high thermal conductivity. When the object enters the atmosphere from outer space, its temperature below its melting point by \[\Delta T\]. Because of atmospheric friction, it absorbs energy at a constant rate of R. The time before the solid becomes completely molten is
A)
\[\frac{M(C+L)\Delta T}{R}\] done
clear
B)
\[\frac{M(C\Delta T+L)}{R}\] done
clear
C)
\[\frac{M(C+L)\Delta T}{R}\] done
clear
D)
\[\frac{R}{(M\Delta T(C+L)}\] done
clear
View Solution play_arrow
-
question_answer8)
\[t={{t}_{1}}+{{t}_{2}}=\frac{M}{R}(C\Delta T+L)\] A glass flask is filled up to a mark with 50 cc of mercury at \[18{}^\circ C\]. If the flask and contents are heated to \[38{}^\circ C,\] how much mercury will be above the mark? (\[\alpha \] for glass is \[9\times {{10}^{-6}}/{}^\circ C\] and coefficient of real expansion of mercury is\[180\times {{10}^{-6}}/{}^\circ C\])
A)
0.85 cc done
clear
B)
0.46 cc done
clear
C)
0.153 cc done
clear
D)
0.05 cc done
clear
View Solution play_arrow
-
question_answer9)
A pendulum clock keeps correct time at \[0{}^\circ C\]. Its mean coefficient of linear expansions is a\[{{\alpha }^{o}}{{C}^{-1}}\]. The loss in seconds per day by the clock if the temperature rises by \[t{}^\circ C\] is
A)
\[\frac{\frac{1}{2}\alpha t\times 864000}{1-\frac{\alpha \,t}{2}}\] done
clear
B)
\[\frac{1}{2}\alpha \,t\times 86400\] done
clear
C)
\[\frac{\frac{1}{2}\alpha \,t\times 86400}{{{\left( 1+\frac{\alpha \,t}{2} \right)}^{2}}}\] done
clear
D)
\[\frac{\frac{1}{2}\alpha \,t\times 86400}{1+\frac{\alpha \,t}{2}}\] done
clear
View Solution play_arrow
-
question_answer10)
The temperature of equal masses of three different liquids A, B and C are \[12{}^\circ C,\] \[19{}^\circ C\] and \[28{}^\circ C\] respectively. The temperature when A and B are mixed is \[16{}^\circ C\] and when B and C are mixed is \[23{}^\circ C,\] The temperature when A and C are mixed is
A)
\[18.2{}^\circ C\] done
clear
B)
\[22{}^\circ C\] done
clear
C)
\[20.2{}^\circ C\] done
clear
D)
\[25.2{}^\circ C\] done
clear
View Solution play_arrow
-
question_answer11)
A constant volume gas thermometer shows pressure reading of 50 cm and 90 cm of mercury at \[0{}^\circ C\] and \[100{}^\circ C\] respectively. When the pressure reading is 60 cm of mercury, the temperature is
A)
\[25{}^\circ C\] done
clear
B)
\[40{}^\circ C~\] done
clear
C)
\[15{}^\circ C\] done
clear
D)
\[{{12.5}^{o}}C\] done
clear
View Solution play_arrow
-
question_answer12)
The volume of a metal ball increases by 0.18% when its temperature is increased by \[{{30}^{o}}C\] What is the coefficient of linear expansion of metal?
A)
\[2\times {{10}^{-5}}{{l}^{0}}C\] done
clear
B)
\[3\times {{10}^{-5}}{{l}^{0}}C\] done
clear
C)
\[6\times {{10}^{-5}}{{l}^{0}}C\] done
clear
D)
\[1.8\times {{10}^{-4}}{{l}^{0}}C\] done
clear
View Solution play_arrow
-
question_answer13)
Steam at \[1\,\,\text{atm}\,\,and\,\,100{}^\circ C\] enters a radiator & leaves as water at \[1\,\,\text{atm}\,\,and\,\,80{}^\circ C,\] take \[{{L}_{y}}=540\text{ cal/cm}\] and \[{{s}_{water}}=11\text{ }cal/gm/{}^\circ C.\] If the total energy given off as heat, the % age arises from the cooling of water is
A)
100 done
clear
B)
54 done
clear
C)
3.6 done
clear
D)
8.2 done
clear
View Solution play_arrow
-
question_answer14)
Compared to a burn due to water at \[100{}^\circ C,\] a burn due of steam at \[100{}^\circ C\] is
A)
More dangerous done
clear
B)
Less dangerous done
clear
C)
Equally dangerous done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer15)
Two rods are joined between fixed supports as shown in the figure. Condition for no change in the lengths of individual rods with the increase of temperature will be (\[{{\alpha }_{1}},{{\alpha }_{2}}\]= linear expansion co-efficient \[{{\text{A}}_{\text{1}}}\text{,}{{\text{A}}_{\text{2}}}\] =Area of rods \[{{\text{Y}}_{\text{1}}}\text{,}{{\text{Y}}_{\text{2}}}\]= Young modulus)
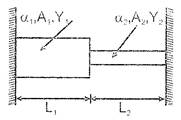
A)
\[\frac{{{\text{A}}_{\text{1}}}}{{{\text{A}}_{\text{2}}}}\text{=}\frac{{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{1}}}{{\text{Y}}_{\text{1}}}}{{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{2}}}{{\text{Y}}_{\text{2}}}}\] done
clear
B)
\[\frac{{{\text{A}}_{\text{1}}}}{{{\text{A}}_{\text{2}}}}\text{=}\frac{{{\text{L}}_{1}}{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{1}}}{{\text{Y}}_{\text{1}}}}{{{\text{L}}_{2}}{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{2}}}{{\text{Y}}_{\text{2}}}}\] done
clear
C)
\[\frac{{{\text{A}}_{\text{1}}}}{{{\text{A}}_{\text{2}}}}\text{=}\frac{{{\text{L}}_{2}}{{\text{ }\!\!\alpha\!\!\text{ }}_{2}}{{\text{Y}}_{2}}}{{{\text{L}}_{1}}{{\text{ }\!\!\alpha\!\!\text{ }}_{1}}{{\text{Y}}_{1}}}\] done
clear
D)
\[\frac{{{\text{A}}_{\text{1}}}}{{{\text{A}}_{\text{2}}}}\text{=}\frac{{{\text{ }\!\!\alpha\!\!\text{ }}_{2}}{{\text{Y}}_{2}}}{{{\text{ }\!\!\alpha\!\!\text{ }}_{1}}{{\text{Y}}_{1}}}\] done
clear
View Solution play_arrow
-
question_answer16)
On an X temperature scale, water freezes at \[-125.0{}^\circ X\] and boils at \[375.0{}^\circ X\]. On a Y temperature scale, water freezes at \[-70.0{}^\circ Y\] and boils at\[-30.0{}^\circ Y\]. The value of temperature on X-scale equal to the temperature of \[50.0{}^\circ Y\] on Y-scale is :
A)
\[455.0{}^\circ X\] done
clear
B)
\[-125.0{}^\circ X\] done
clear
C)
\[1375.0{}^\circ X\] done
clear
D)
\[1500.0{}^\circ X\] done
clear
View Solution play_arrow
-
question_answer17)
An ice block at \[0{}^\circ C\] and of mass m is dropped from height 'h' such that the loss in gravitational potential energy of block is exactly equal to the heat required to just completely melt the ice. Taking latent heat of fusion of ice \[=\text{ }80\text{ }cal/gm,\] acceleration due to gravity \[=\text{ }10\text{ }m/{{s}^{2}}\] and, mechanical equivalent of heat \[=\text{ }4.2\text{ }J/Cal\]. The value of 'h' is
A)
8 m done
clear
B)
8 km done
clear
C)
33.6 m done
clear
D)
33.6 km done
clear
View Solution play_arrow
-
question_answer18)
4 gms of steam at \[100{}^\circ C\] is added to 20 gms of water at \[46{}^\circ C\] in a container of negligible mass. Assuming no heat is lost to surrounding, the mass of water in container at thermal equilibrium is. Latent heat of vaporisation \[=\text{ }540\text{ }cal/gm\]. Specific heat of water \[=\text{ }1\text{ }cal/gm-{}^\circ C\].
A)
18gm done
clear
B)
20gm done
clear
C)
22gm done
clear
D)
24gm done
clear
View Solution play_arrow
-
question_answer19)
A uniform metallic object of circular shape which is free to expand in every direction is shown in figure. The parameter which will not increase on heating the object is :
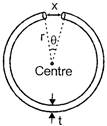
A)
x (gap) done
clear
B)
r (radius of circle) done
clear
C)
\[\theta \] (angle formed at centre) done
clear
D)
t(thickness) done
clear
View Solution play_arrow
-
question_answer20)
Mercury is poured in a U tube. Level of mercury on one side is \[{{h}_{1}}\] at temperature \[\text{5}{{\text{0}}^{\text{o}}}\text{C}\] and level of mercury on the other side is \[{{h}_{2}}\] at temperature \[\text{10}{{\text{0}}^{\text{o}}}\text{C}\] Then
A)
\[{{h}_{1}}={{h}_{2}}\] done
clear
B)
\[{{h}_{1}}<{{h}_{2}}\] done
clear
C)
\[{{h}_{1}}>{{h}_{2}}\] done
clear
D)
\[{{h}_{2}}=2{{h}_{1}}\] done
clear
View Solution play_arrow
-
question_answer21)
If two rods of length L and 2L having coefficients of linear expansion \[\alpha \] and \[2\alpha \] respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals :
A)
\[\frac{3}{2}\alpha \] done
clear
B)
\[\frac{5}{2}\alpha \] done
clear
C)
\[\frac{5}{3}\alpha \] done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer22)
A steel scale is calibrated for\[\text{27}{{\,}^{\text{o}}}\text{C}\text{.}\] The error in a reading of 50 cm at\[30{{\,}^{\text{o}}}\text{C}\]is \[[{{\alpha }_{steel}}=1.2\,\times \,{{10}^{-5}}/{{\,}^{o}}C]\]
A)
0.018 mm done
clear
B)
0.18 mm done
clear
C)
0.0018 mm done
clear
D)
0.16 mm done
clear
View Solution play_arrow
-
question_answer23)
Four cubes of ice at \[-10{}^\circ C\] each one gm is taken out from the refrigerator and are put in 150 gm of water at \[20{}^\circ C\]. The temperature of water when thermal equilibrium is attained. Assume that no heat is lost to the outside and water equivalent of container is 46 gm. (Specific heat capacity of water \[=\text{ }1\text{ }cal/gm-{}^\circ C\], Specific heat capacity of ice \[=\text{ }0.5\text{ }cal/gm-{}^\circ C\], Latent heat of fusion of ice \[=\text{ }80\text{ }cal/gm)\]
A)
\[0{}^\circ C\] done
clear
B)
\[-10{}^\circ C\] done
clear
C)
\[17.9{}^\circ C\] done
clear
D)
None done
clear
View Solution play_arrow
-
question_answer24)
The freezing point on a thermometer is marked as -\[{{20}^{\circ }}\]and the boiling point as \[{{130}^{\circ }}\]. A temperature of human body \[({{34}^{\circ }}C)\]on this thermometer will be read as:
A)
\[{{31}^{\circ }}\] done
clear
B)
\[{{51}^{\circ }}\] done
clear
C)
\[{{20}^{\circ }}\] done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer25)
A circular hole is made in a plate. The plate is now heated. Which of the following statements is/are correct?
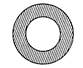
A)
radius of the hole starts to decrease done
clear
B)
no stress is developed in the material of plate done
clear
C)
volume of the plate material will decrease done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer26)
When a building is constructed at \[-10{}^\circ C\], a steel beam (cross-sectional area \[45\text{ }c{{m}^{2}}\]) is put in place with its ends cemented in pillars. If the sealed ends cannot move, what will be the compressional force in the beam when the temperature is \[25{}^\circ C\]? For this kind of steel, \[\alpha =1.1\times {{10}^{-5}}\,{{\,}^{o}}{{C}^{-1}}\] and \[Y=2.0\times {{10}^{11}}N/{{m}^{2}}\].
A)
\[2.5\times {{10}^{3}}N\] done
clear
B)
\[3.5\times {{10}^{5}}N\] done
clear
C)
\[2.5\times {{10}^{5}}N\] done
clear
D)
\[3.5\times {{10}^{3}}N\] done
clear
View Solution play_arrow
-
question_answer27)
If the length of a cylinder on heating increases by 2%, the area of its base will increase by-
A)
0.5% done
clear
B)
2% done
clear
C)
1% done
clear
D)
4% done
clear
View Solution play_arrow
-
question_answer28)
The thermal capacity of 40 g of aluminium (specific heat \[-\,0.2cal/\,gm{}^\circ C)\])
A)
\[40cal/{}^\circ C\] done
clear
B)
\[160cal/{}^\circ C\] done
clear
C)
\[200cal/{}^\circ C\] done
clear
D)
\[8cal/{}^\circ C\] done
clear
View Solution play_arrow
-
question_answer29)
A wooden cylinder of 50 kg is floating in water. A weight of 2 kg is to be placed on it to just make it submerge when the temperature is \[10{}^\circ C\]. How much less weight is to be placed when temperature increases to \[30{}^\circ C\]? (Given \[{{\gamma }_{water}}={{10}^{-4}}{{/}^{o}}C,{{\gamma }_{wood}}\] is negligible.):
A)
104 g done
clear
B)
58 g done
clear
C)
208 g done
clear
D)
54 g done
clear
View Solution play_arrow
-
question_answer30)
| DIRECTION: Read the passage given below and answer the questions that follows: |
| In a thermally insulated tube of cross sectional area \[\frac{GMm}{2R}\] a liquid of thermal expansion coefficient \[{{10}^{-3}}\,{{K}^{-1}}\] is flowing. Its velocity at the entrance is \[0.1\text{ }m/s\]. At the middle of the tube a heater of a power of 10kW is heating the liquid. The specific heat capacity of the liquid is 1.5 kJ/(kg K), and its density is \[1500\text{ }kg/{{m}^{3}}\] at the entrance. |
The rise in temperature of the liquid as it pass through the tube is
A)
\[\frac{1000}{9}{}^\circ C\] done
clear
B)
\[\frac{1}{9}{}^\circ C\] done
clear
C)
\[\frac{500}{9}{}^\circ C\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer31)
| DIRECTION: Read the passage given below and answer the questions that follows: |
| In a thermally insulated tube of cross sectional area \[\frac{GMm}{2R}\] a liquid of thermal expansion coefficient \[{{10}^{-3}}\,{{K}^{-1}}\] is flowing. Its velocity at the entrance is \[0.1\text{ }m/s\]. At the middle of the tube a heater of a power of 10kW is heating the liquid. The specific heat capacity of the liquid is 1.5 kJ/(kg K), and its density is \[1500\text{ }kg/{{m}^{3}}\] at the entrance. |
What is the density of liquid at the exit?
A)
1450 kg/m3 done
clear
B)
1400 kg/m3 done
clear
C)
1350 kg/m3 done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer32)
How much bigger is the volume rate of flow at the end of the tube than at the entrance in cubic meters?
A)
\[9\,\times \,{{10}^{-5}}\] done
clear
B)
\[\frac{1}{3}\times \,{{10}^{-5}}\] done
clear
C)
\[\frac{4}{9}\times \,{{10}^{-5}}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer33)
The coefficient of apparent expansion of a liquid in a copper vessel is C and in a silver vessel S. The coefficient of volume expansion of copper is \[{{\gamma }_{C}}\]. What is the coefficient of linear expansion of silver?
A)
\[(C+{{\gamma }_{C}}+S)/3\] done
clear
B)
\[(C-{{\gamma }_{C}}+S)/3\] done
clear
C)
\[(C+{{\gamma }_{C}}-S)/3\] done
clear
D)
\[(C-{{\gamma }_{C}}-S)/3\] done
clear
View Solution play_arrow
-
question_answer34)
A piece of metal weight 46 gm in air, when it is immersed in the liquid of specific gravity 1.24 at \[27{}^\circ C\] it weighs 30 gm. When the temperature of liquid is raised to \[42{}^\circ C\], the metal piece weighs 30.5 gm, specific gravity of the liquid at \[42{}^\circ C\] is 1.20, then the linear expansion of the metal will be
A)
\[3.316\,\times \,{{10}^{-5}}\,/{}^\circ C\] done
clear
B)
\[2.316\,\times \,{{10}^{-5}}\,/{}^\circ C\] done
clear
C)
\[4.316\,\times \,{{10}^{-5}}\,/{}^\circ C\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer35)
2 kg of ice at \[\text{ }20{}^\circ C\] is mixed with 5kg of water at \[20{}^\circ C\] in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water and ice are \[1\text{ }kcal/kg\text{ }/{}^\circ C\] and \[0.5\text{ }kcal/kg/{}^\circ C\] while the latent heat of fusion of ice is 80 kcal/kg
A)
7kg done
clear
B)
6kg done
clear
C)
4kg done
clear
D)
2kg done
clear
View Solution play_arrow
