-
Find
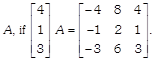
-
Find a vector in the direction of a vector \[\vec{a}=-\,\hat{i}-\hat{j}+\hat{k},\] which has magnitude 8 units. \[\vec{a}=\hat{i}-\hat{j}+\hat{k},\] which has magnitude 8 units.
View Answer play_arrow
-
Let f : \[R\to R:f(x)=({{x}^{2}}-3x+2).\] Find fof(x).
View Answer play_arrow
-
Let A = {0, 1, 2, 3} and define a relation R or A as follows R = {(0, 0)(0, 1)(0, 3)(1, 0)(1, 1)(2, 2)(3, 0)(3, 3)}. Is R reflexive, symmetric and transitive?
View Answer play_arrow
-
Show that the points \[(a+5,\,\,a-4),\] \[(a-2,\,\,a+3)\] and (a, a) do not lie on a straight line for any value of a.
View Answer play_arrow
-
If \[P(A)=\frac{1}{4,}\] \[P(B)=\frac{1}{5}\] and \[P(A\,\cap B)=\frac{1}{7},\]find \[P(\bar{A}\,/\bar{B}).\]
View Answer play_arrow
-
Determine f(0), so that the function f(x) defined by \[f(x)=\frac{{{({{4}^{x}}-1)}^{3}}}{\sin \frac{x}{4}\log \left( 1+\frac{{{x}^{2}}}{3} \right)}\] becomes continuous at x = 0.
View Answer play_arrow
-
If x changes from 3 to 3.3, find the approximate change in log e (1 + x).
View Answer play_arrow
-
If \[y={{\cot }^{-1}}(\sqrt{\cos \,x})-ta{{n}^{-1}}(\sqrt{\cos \,x}),\] prove that \[\sin y={{\tan }^{2}}\frac{x}{2}.\]
View Answer play_arrow
-
If \[y=b{{\tan }^{-1}}\left( \frac{x}{a}+{{\tan }^{-1}}\frac{y}{x} \right),\] find \[\frac{dy}{dx}.\]
View Answer play_arrow
-
Evaluate \[\int{\tan (x-\theta )\tan (x+\theta )\tan 2x\,dx.}\]
View Answer play_arrow
-
Find the position vector of a point R which divides the line joining the points \[P(\hat{i}\,+2\hat{j}\,-\hat{k})\] and \[Q(-\hat{i}\,+\hat{j}\,+\hat{k})\] in the ratio 2 : 1 (i) Internally. (ii) externally.
View Answer play_arrow
-
Find the shortest distance between lines \[\frac{x-3}{1}=\frac{y-5}{-\,2}=\frac{z-7}{1}\] and \[\frac{x+1}{7}=\frac{y+1}{-\,6}=\frac{z+1}{1}.\]
View Answer play_arrow
-
Find the particular solution of the differential equation \[(1+{{e}^{2x}})\,dy+(1+{{y}^{2}}){{e}^{x}}dx=0,\] given that y = 1 when x = 0.
View Answer play_arrow
-
Show that the differential equation that represents the family of all parabolas having their axis of symmetry coincident with the axis of x is \[y{{y}_{2}}+y_{1}^{2}=0.\]
View Answer play_arrow
-
Evaluate \[\int_{0}^{1}{{{e}^{3x-2}}dx.}\]
View Answer play_arrow
-
| Evaluate \[\int{\sqrt{3-4x-4{{x}^{2}}}\,\,dx.}\] |
| OR |
| Evaluate \[\int{\frac{\sin (x-\alpha )}{\sin (x+\alpha )}\,dx.}\] |
View Answer play_arrow
-
To raise money for an orphanage, students of three schools A, B and C organised an exhibition in their locality, where they sold paper bags, scrap-books and postel-sheets made by them using recycled paper, at the rate of Rs. 20, Rs. 15 and Rs. 5 per unit, respectively. School A sold 25 paper bags, 12 scrap-books and 34 postel-sheets. School B sold 22 paper bags, 15 scrap-books and 28 postel-sheets, while school C sold 26 paper bags, 18 scrap-books and 36 postel-sheets. Using matrices, find the total amount raised by each school. By such exhibition, which values are inculcated in the students?
View Answer play_arrow
-
| If \[{{x}^{y}}+{{y}^{x}}={{a}^{b}},\] then find \[\frac{dy}{dx}.\] |
| OR |
| If \[y=\log [x+\sqrt{{{x}^{2}}+{{a}^{2}}}],\] show that \[({{x}^{2}}+{{a}^{2}})\frac{{{d}^{2}}y}{d{{x}^{2}}}+x\frac{dy}{dx}=0.\] |
View Answer play_arrow
-
Find the intervals in which the function \[f(x)=2{{x}^{3}}-15{{x}^{2}}+36x+17\] is increasing or decreasing.
View Answer play_arrow
-
Prove that \[a\cdot (b+c)\times (a+2b+3c)=[\begin{matrix} a & b & c \\ \end{matrix}].\]
View Answer play_arrow
-
| Find the mean and variance of number of tails when a coin is tossed thrice. |
| OR |
| 12 cards numbered 1 to 12 are placed in a box, mixed up thoroughly and then a card is drawn at random from the box. |
| If it is known that the number on the drawn card is more than 3, then find the probability that it is an even number. |
View Answer play_arrow
-
Three bags contain a number of red and white balls as follows Bag I: 3 red balls, Bag II: 2 red balls and 1 white ball and Bag III: 3 white balls. The probability that bag will be chosen and a ball is selected from it is \[\frac{i}{6},\] where i =1, 2, 3. (i) What is the probability that a red ball is selected? (ii) If a white ball is selected, then, what is the probability that it came from bag III?
View Answer play_arrow
-
Find the area of the region bounded by the parabola \[{{x}^{2}}=4y\] and the line \[x=4y-2.\]
View Answer play_arrow
-
Let T be the set of all triangles in a plane. Let us define a relation \[R=\{({{T}_{1}},\,\,{{T}_{2}}):{{T}_{1}}\,\,is\,\,similar\,\,to\,\,{{T}_{2}};{{T}_{1}},\,{{T}_{2}}\in T\}.\] Show that R is an equivalence relation.
View Answer play_arrow
-
| For the curve \[y=4{{x}^{3}}-2{{x}^{5}},\] find all the point on the curve at which the tangent passes through the origin, |
| OR |
| Show that of all the rectangles with a given perimeter, the square has the largest area. |
View Answer play_arrow
-
| Find the image of point (1, 0, 0) on the line \[\frac{x}{1}=\frac{y}{2}=\frac{z}{3}.\] |
| OR |
| Find the equation of the plane that contains the point \[(1,\,\,-\,1,\,\,2)\] and is perpendicular to both the planes \[2x+3y-2z=5\]and \[x+2y-3z=8.\] |
| Hence, find the distance of point \[P(-\,2,\,\,5,\,\,5)\] from the plane obtained above. |
View Answer play_arrow
-
An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 1000 is made on each executive class ticket and a profit of Rs. 600 is made on each economy class ticket. The airline donate its 5% of total profit in welfare fund for poor girls. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class, then by executive class. Determine how many tickets of each type must be sold in order to maximize profit for the airline? What is the maximum profit? Do you think, more passengers would prefer to travel by such an airline then by others?
View Answer play_arrow
-
| Show that \[\Delta ABC\] is an isosceles triangle, if the determinant |
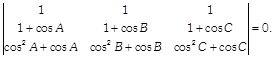 |
| OR |
| If \[A+B+C=\pi ,\] show that |
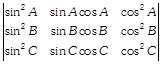 \[=-\sin (A-B)\sin (B-C)\sin (C-A)\] \[=-\sin (A-B)\sin (B-C)\sin (C-A)\] |
View Answer play_arrow
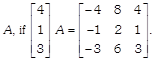
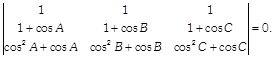
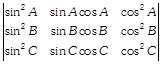 \[=-\sin (A-B)\sin (B-C)\sin (C-A)\]
\[=-\sin (A-B)\sin (B-C)\sin (C-A)\] 