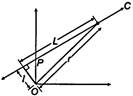
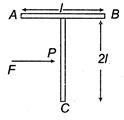
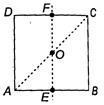
| For the given uniform square lamina ABCD, whose centre is O [AIEEE 2007] |
 |
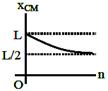
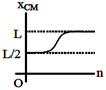
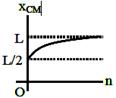
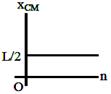
| A small particle of mass m is projected at an angle\[\theta \]with the x-axis with an initial velocity v0 in the\[x-y\]plane as shown in the figure. At a time \[t<\frac{{{v}_{0}}\sin \theta }{g},\] the angular momentum of the particle is - [AIEEE 2010] |
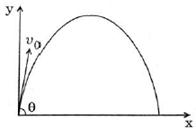 |
|
done
clear
C)
\[\frac{2}{5}\]rotational and \[\frac{3}{5}\]translational
done
clear
D)
\[\frac{1}{2}\]rotational and \[\frac{1}{2}\]translational
done
clear
View Answer play_arrow
question_answer32)
A)
\[\sqrt{2gh}\]
done
clear
B)
\[\sqrt{\frac{7}{5}gh}\]
done
clear
C)
\[\sqrt{\frac{7}{2}gh}\]
done
clear
D)
\[\sqrt{\frac{10}{7}gh}\]
done
clear
View Answer play_arrow
question_answer33)
A)
Statement 1 is true, Statement 2 is true, Statement 2 is not the correct explanation of Statement 1.
done
clear
B)
Statement 1 is false, Statement 2 is true.
done
clear
C)
Statement 1 is true, Statement 2 is true. Statement 2 is correct explanation of the Statement 1.
done
clear
D)
Statement 1 is true, Statement 2 is false.
done
clear
View Answer play_arrow
question_answer34) A stone of mass m, tied to the end of a string, is whirled around in a circle on a horizontal frictionless table. The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by \[T=A{{r}^{n}},\]where A is a constant, r is the instantaneous radius of the circle. The value of n is equal to [JEE ONLINE 26-05-2012]
A)
- 1
done
clear
B)
- 2
done
clear
C)
- 4
done
clear
D)
- 3
done
clear
View Answer play_arrow
question_answer35) A thick-walled hollow sphere has outside radius \[{{R}_{0}}.\]It rolls down an incline without slipping and its speed at the bottom is \[{{v}_{0}}.\] Now the incline is waxed, so that it is practically frictionless and the sphere is observed to slide down (without any rolling). Its speed at the bottom is observed to be \[5{{v}_{0}}/4.\]The radius of gyration of the hollow sphere about an axis through its centre is [JEE ONLINE 26-05-2012]
A)
\[3{{R}_{0}}/2\]
done
clear
B)
\[3{{R}_{0}}/4\]
done
clear
C)
\[9{{R}_{0}}/16\]
done
clear
D)
\[3{{R}_{0}}\]
done
clear
View Answer play_arrow
question_answer36) A hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip? [JEE MAIN 2013]
A)
\[\frac{r{{\omega }_{0}}}{4}\]
done
clear
B)
\[\frac{r{{\omega }_{0}}}{3}\]
done
clear
C)
\[\frac{r{{\omega }_{0}}}{2}\]
done
clear
D)
\[r{{\omega }_{0}}\]
done
clear
View Answer play_arrow
question_answer37) A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 Kg. It is hinged at one end and rotates about a vertical axis practically without friction. The angular speed of the door just ager the bullet embeds into it will be: [JEE ONLINE 09-04-2013]
A)
6.25 rad/sec
done
clear
B)
0.625 rad/sec
done
clear
C)
3.35 rad/sec
done
clear
D)
0.335 rad/sec
done
clear
View Answer play_arrow
question_answer38) A tennis ball (treated as hollow spherical shell) starting from O rolls down a hill. At point A the ball becomes air borne leaving at an angle of \[{{30}^{0}}\] with the horizontal. The ball strikes the ground at B. What is the value of the distance AB? (Moment of inertia of spherical shell of mass m and radius R about its diameter \[=\frac{2}{3}{{\operatorname{mR}}^{2}})\] [JEE ONLINE 22-04-2013]
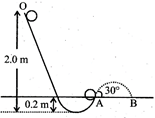
A)
1.87 m
done
clear
B)
2.08 m
done
clear
C)
1.57 m
done
clear
D)
1.77 m
done
clear
View Answer play_arrow
question_answer39) A particle of mass 2 kg is moving such hat at time t, its position, in meter, is given by \[\overset{\to }{\mathop{\operatorname{r}}}\,(\operatorname{t})=5\hat{i}-2{{\operatorname{t}}^{2}}\hat{j}.\] The angular momentum of the particle at \[\operatorname{t}=2s\] about the origin in kg \[{{\operatorname{m}}^{-2}}\]\[{{\operatorname{s}}^{-2}}\] is: [JEE ONLINE 23-04-2013]
A)
\[-80\hat{k}\]
done
clear
B)
\[\left( 10\hat{i}-16\hat{j} \right)\]
done
clear
C)
\[-40\hat{k}\]
done
clear
D)
\[40\hat{k}\]
done
clear
View Answer play_arrow
question_answer40) A boy of mass 20 kg is standing on a 80 kg free to move long cart. There is negligible friction between cart and ground. Initially, the boy is standing 25 m from a wall. If he walks 10 m on the cart toward the wall, then the final distance of the boy from the wall will be: [JEE ONLINE 23-04-2013]
A)
15 m
done
clear
B)
12.5 m
done
clear
C)
15.5 m
done
clear
D)
17 m
done
clear
View Answer play_arrow
question_answer41) A 70 Kg man leaps vertically into the air from a crouching position. To take the leap the man pushes the pushes the ground with a constant force F to raise himself. The center of gravity rises by 0.5 m before he leaps. After the leap the c.g. rises by another 1 m. The maximum power delivered by the muscles is: (Take g = 10 \[\text{m}{{\text{s}}^{\text{2}}}\]). [JEE ONLINE 23-04-2013]
A)
\[\text{6}\text{.26}\times \text{1}{{\text{0}}^{\text{3}}}\] Watts at the start
done
clear
B)
\[\text{6}\text{.26}\times \text{1}{{\text{0}}^{\text{3}}}\] Watts at take off
done
clear
C)
\[\text{6}\text{.26}\times \text{1}{{\text{0}}^{\text{4}}}\] Watts at the start
done
clear
D)
\[\text{6}\text{.26}\times \text{1}{{\text{0}}^{\text{4}}}\] Watts at take off
done
clear
View Answer play_arrow
question_answer42) A ring of mass M and radius R is rotating about its axis with angular velocity \[\omega \]. Two identical bodies each of mass m are now gently attached at the two ends of a diameter of the ring. Because of this, the kinetic energy loss will be: [JEE ONLINE 25-04-2013]
A)
\[\frac{\operatorname{m}(\operatorname{M}+2m)}{\operatorname{M}}{{\omega }^{2}}{{R}^{2}}\]
done
clear
B)
\[\frac{\operatorname{Mm}}{(\operatorname{M}+m)}{{\omega }^{2}}{{R}^{2}}\]
done
clear
C)
\[\frac{\operatorname{Mm}}{(\operatorname{M}+2m)}{{\omega }^{2}}{{R}^{2}}\]
done
clear
D)
\[\frac{\left(\operatorname{M}+m \right)\operatorname{M}}{(\operatorname{M}+2m)}{{\omega }^{2}}{{R}^{2}}\]
done
clear
View Answer play_arrow
question_answer43) A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed \[\omega \]rad/s about the vertical. About the point of suspension: [JEE MAIN 2014]
A)
angular momentum changes in direction but not in magnitude.
A)
\[\left( \frac{7}{12}m,\frac{\sqrt{3}}{8}m \right)\]
done
clear
B)
\[\left( \frac{\sqrt{3}}{4}m,\frac{5}{12}m \right)\]
done
clear
C)
\[\left( \frac{7}{12}m,\frac{\sqrt{3}}{4}m \right)\]
done
clear
D)
\[\left( \frac{\sqrt{3}}{8}m,\frac{7}{12}m \right)\]
done
clear
View Answer play_arrow
question_answer108) The radius of gyration of a uniform rod of length l, about an axis passing through a point \[\frac{l}{\text{4}}\] away from the centre of the rod, and perpendicular to it, is: [JEE MAIN Held on 07-01-2020 Morning]
A)
\[\sqrt{\frac{\text{7}}{\text{48}}}l\]
done
clear
B)
\[\frac{\text{1}}{\text{8}}l\]
done
clear
C)
\[\frac{1}{4}l\]
done
clear
D)
\[\sqrt{\frac{\text{3}}{\text{8}}}l\]
done
clear
View Answer play_arrow
question_answer109)
A)
\[r\sqrt{\frac{3}{2gh}}\]
done
clear
B)
\[r\sqrt{\frac{3}{4gh}}\]
done
clear
C)
\[\frac{1}{r}\sqrt{\frac{4gh}{3}}\]
done
clear
D)
\[\frac{1}{r}\sqrt{\frac{2gh}{3}}\]
done
clear
View Answer play_arrow
question_answer110)
A)
1.5 cm right and 1.2 cm above 1 kg mass
done
clear
B)
2.0 cm right and 0.9 cm above 1 kg mass
done
clear
C)
0.9 cm right and 2.0 cm above 1 kg mass
done
clear
D)
0.6 cm right and 2.0 cm above 1 kg mass
done
clear
View Answer play_arrow
question_answer111) Mass per unit area of a circular disc of radius a depends on the distance r from its centre as\[\sigma \,(r)=A+Br\]. The moment of inertia of the disc about the axis, perpendicular to the plane and passing through its centre is: [JEE MAIN Held on 07-01-2020 Evening]
A)
\[2\pi {{a}^{4}}\,\left( \frac{A}{4}+\frac{B}{5} \right)\]
done
clear
B)
\[\pi {{a}^{4}}\,\left( \frac{A}{4}+\frac{aB}{5} \right)\]
done
clear
C)
\[2\pi {{a}^{4}}\,\left( \frac{A}{4}+\frac{aB}{5} \right)\]
done
clear
D)
\[2\pi {{a}^{4}}\,\left( \frac{aA}{4}+\frac{B}{5} \right)\]
done
clear
View Answer play_arrow
question_answer112) An elevator in a building can carry a maximum of 10 persons, with the average mass of each person being 68 kg. The mass of the elevator itself is 920 kg and it moves with a constant speed of 3 m/s. The frictional force opposing the motion is 6000 N. If the elevator is moving up with its full capacity, the power delivered by the motor to the elevator \[(g=10\text{ }m/{{s}^{2}})\]must be at least [JEE MAIN Held on 07-01-2020 Evening]
A)
56300 W
done
clear
B)
66000 W
done
clear
C)
48000 W
done
clear
D)
62360 W
done
clear
View Answer play_arrow
question_answer113)
View Answer play_arrow
question_answer114)
A)
\[\left( 0.75\text{ }m,\text{ }1.75\text{ }m \right)\]
done
clear
B)
\[\left( 1.25\text{ }m,\text{ }1.50\text{ }m \right)\]
done
clear
C)
\[\left( 1\text{ }m,\text{ }1.75\text{ }m \right)\]
done
clear
D)
\[\left( 0.75\text{ }m,\text{ }0.75\text{ }m \right)\]
done
clear
View Answer play_arrow
question_answer115) Consider a uniform rod of mass M = 4 m and length l pivoted about its centre. A mass moving with velocity v making angle\[\theta =\frac{\pi }{4}\]to the rods long axis collides with one end of the rod and sticks to it. The angular speed of the rod-mass system just after the collision is [JEE MAIN Held On 08-01-2020 Morning]
A)
\[\frac{4}{7}\frac{V}{l}\]
done
clear
B)
\[\frac{3}{7}\frac{V}{l}\]
done
clear
C)
\[\frac{3}{7\sqrt{2}}\frac{V}{l}\]
done
clear
D)
\[\frac{3\sqrt{2}}{7}\frac{V}{l}\]
done
clear
View Answer play_arrow
question_answer116) A uniform sphere of mass 500 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is [JEE MAIN Held on 08-01-2020 Evening]
A)
\[6.25\times {{10}^{4}}J\]
done
clear
B)
\[1.13\times {{10}^{3}}J\]
done
clear
C)
\[8.75\times {{10}^{\,4}}\text{ }J\]
done
clear
D)
\[8.75\times {{10}^{3}}\text{ }J\]
done
clear
View Answer play_arrow
question_answer117) A particle of mass m is dropped from a height h above the ground. At the same time another particle of the same mass is thrown vertically upwards from the ground with a speed of\[\sqrt{2gh}\]. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of \[\sqrt{\frac{h}{g}}\] is [JEE MAIN Held on 08-01-2020 Evening]
A)
\[\sqrt{\frac{1}{2}}\]
done
clear
B)
\[\sqrt{\frac{3}{4}}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[\sqrt{\frac{3}{2}}\]
done
clear
View Answer play_arrow
question_answer118)
A)
\[\left( {{R}^{2}}\text{+}R+1 \right)\left( 2R \right)=1\]
done
clear
B)
C)
D)
question_answer119)
A)
B)
C)
D)
question_answer120)
View Answer play_arrow
question_answer121) A rod of length L has non-uniform linear mass density given by
A)
B)
C)
D)
question_answer122)
A)
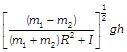
B)
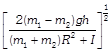
C)
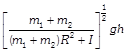
D)
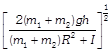 Study Package
You need to login to perform this action. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||