MENSURATION
Category : 7th Class
Learning Objectives:
PERIMETER AND AREA
PERIMETER:
Perimeter is the total boundary length of a closed figure.
The commonly used units of perimeter are kilometer, meter and centimeter.
|
Shape |
Total no. of sides |
Perimeter |
|
1. Square |
4 |
4\[\times \]length of a side |
|
2. Rectangle |
2 length 2 width |
2\[\times \]length + 2 \[\times \]width = 2 (length + width) |
|
3. Triangle (Equilateral) |
3 |
3\[\times \]length of a side |
|
4. Triangle (isosceles) |
2 equal 1 unequal |
2\[\times \]length of equal sides + 1 length of different side |
|
5. Triangle (Scalene) |
3 (all unequal) |
Sum of all unequal sides |
Example: Find the perimeter of
Solution:
Perimeter\[=4\times \]side
\[=4\times 2.5\]
\[=10\,m\]
Perimeter\[=2\,(\ell +w)\]
\[=2\,(30+30)\]
\[=2\times 50\]
\[=100\,cm\]
Perimeter = 2 + 3 + 5
= 10 cm.
AREA:
Area is the amount of surface covered by any shape
|
|
Shape |
Area |
|
1. |
Square |
side\[\times \]side |
|
2. |
Rectangle |
length\[\times \]breadth |
|
3. |
Triangle |
\[\frac{1}{2}\]\[\times \]base\[\times \]height |
|
4. |
Equilateral triangle |
\[\frac{\sqrt{3}}{4}\times \text{sid}{{\text{e}}^{2}}\] |
|
5. |
Parallelogram |
base\[\times \]height |
Example:
(i) Find the area of square with side 4 cm.
Solution: Area = side\[\times \]side
\[=4\times 4\]
\[=16\,c{{m}^{2}}\]
(ii) Find the area of rectangle whose \[\ell ~=4\,cm,\] \[b=6\,cm\]
Solution: Area\[=\ell \times b\]
\[=4\times 6=24\,c{{m}^{2}}\]
(iii) Find the area of triangle with \[b=5\,cm,\]\[h=2.5\,cm\]
Solution: \[\Delta \]Area \[=\frac{1}{2}\times b\times h\]
\[=\frac{1}{2}\times 5\times 2.5\]
\[=6.25\,c{{m}^{2}}\]
Solution: Area of parallelogram = Base\[\times \]height
\[=7\times 5=35\,c{{m}^{2}}\]
Areas of Rectangular Path:
Type 1: Paths running around (inside/outside) a rectangular shape.
Rule 1: When the path runs outside, twice the width of the path should be added to length and breadth of the inner rectangle.
Measures of Area:
\[1\,cm=10\,mm\Rightarrow 1\,c{{m}^{2}}=10\,mm\times 10\,mm=100\,m{{m}^{2}}\]
\[1\,dm=10\,cm\Rightarrow 1\,d{{m}^{2}}=10\,cm\times 10\,cm=100\,c{{m}^{2}}\]
\[1\,m=100\,cm\Rightarrow 1\,{{m}^{2}}=100\,cm\times 100\,cm=10,000\,c{{m}^{2}}\]
\[1\,dam=10\,m\Rightarrow 1\,da{{m}^{2}}=10\,m\times 10\,m=100\,{{m}^{2}}\]
\[1\,km=1000\,m\Rightarrow 1\,k{{m}^{2}}=1000\,m\times 1000\,m=10,00,000\,{{m}^{2}}\]
\[1\,Arc=10\,m\times 10\,m=100\,{{m}^{2}}\]
\[1\,hectare\,(1\,ha)=100\,m\times 100\,m=10,000\,{{m}^{2}}\]
Example: A garden is 80 m long and 65 m broad. A path 5 m wide is to be fruit outside all around it along its border. Find the area of the path.
Solution: Let ABCD represents the garden and dotted region is 5m path around it
Area of path = Area of EFGH – Area of ABCD
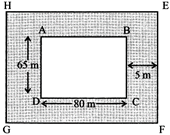
HG = (65 + 5 + 5) m = 75 m
HE = (80 + 5 + 5) m = 90 m
Area of EFGH\[=90\times 75=6750\,{{m}^{2}}\]
Area of ABCD\[=80\times 65=5200\text{ }{{m}^{2}}\]
Area of path\[=6750-5200\]
\[=1550\,{{m}^{2}}\]
Rule 2: When the path runs inside, twice the width of path should be subtracted from the length and breadth of the outer rectangle.
Example: A path 2 m wide is built along the border inside a square park of side 20 m. Find the cost of covering the remaining portion of the park by grass at the rate of Rs. 2/sq. m.
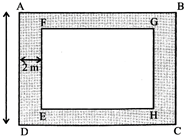
Solution: Let ABCD is a park, dotted portion is 2 m wide path. The plain portion EFGH is remaining part of the park.
\[\text{EF}=(20-1-1)\,m=18\,m\]
\[\text{EH}=(20-1-1)\,m=18\,m\]
Area of remaining portion EFGH\[=18\times 18=324\,{{m}^{2}}\]
Area of park ABCD\[=20\times 20\,{{m}^{2}}\]
\[=400\,{{m}^{2}}\]
Area of dotted portion = Area of ABCD \[-\] Area of EFGH
\[=400-324=76\,{{m}^{2}}\]
Cost of covering \[76\,{{m}^{2}}\]area by grass\[=76\times 2=\text{Rs}\text{.}\,152\]
Type 2: Central paths, i.e. when paths are constructed in the center of the field.
Example: A grassy plot is \[80m\times 50m.\] Two cross paths each 4m wide are constructed at right angles through the center of the field, such that each path is parallel to one of the sides of the rectangle. Find the total area used as path.
Solution: From the figure:
Area of EFGH \[=\left( 80\times 4 \right){{m}^{2}}=320\,{{m}^{2}}\]
Area of PQRS \[=\left( 50\times 4 \right){{m}^{2}}=200\,{{m}^{2}}\]
Area of Common Square \[=\left( 4\times 4 \right)\,c{{m}^{2}}=16\,{{m}^{2}}\]
Area of cross path\[=\left( 320+200-16 \right){{m}^{2}}\]
\[=504\,{{m}^{2}}\]
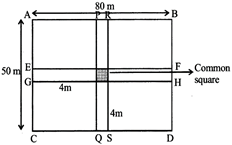
Note: From above fig. it is clear that darker region has been considered twice, because it has been include in both parts EFGH and PQSR. So in order to get the total area of the cross paths, we need to subtract this area from the sum of the areas of the two paths.
AREA OF PARALLELOGRAM:
Example: Find the area of parallelogram with base 7 cm and altitude 4.3 cm.
Solution: Area of parallelogram = Base\[\times \]altitude
\[=7\,cm\times 4.3\,cm\]
\[=30.1\,c{{m}^{2}}\]
Example: A field is in form of parallelogram, has one of its diagonal 40 m long and the perpendicular distance of this diagonal from either of the outlying vertices is 10 m. Find the area of the field.
Solution: Diagonal AC = 42 m.
BE = DF = 10 m.
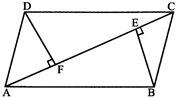
Area of parallelogram = Area of\[\Delta \,ABC\]+ Area of\[\Delta ADC\]
\[=\frac{1}{2}\times AC\times BE+\frac{1}{2}\times AC\times DF\]
\[=\frac{1}{2}\times 42\times (10+10)\]
\[=\frac{1}{2}\times 42\times 20\]
\[=420\,{{m}^{2}}\]
AREA OF TRIANGLE:
Example: Find the area of triangle, whose base is 9.6cm and altitude is 5 cm.
Solution: Area of triangle\[=\frac{1}{2}\times \] base\[\times \]height
\[=\frac{1}{2}\times 9.6\times 5\]
\[=24\,c{{m}^{2}}\]
AREA OF EQUILATERAL TRIANGLE:
Example: Find the area of equilateral triangle whose one side is 5 cm.
Solution: Area of equilateral triangle\[=\frac{\sqrt{3}}{4}\times \text{sid}{{\text{e}}^{2}}\]
\[=\frac{\sqrt{3}}{4}\times 5\times 5\]
\[=10.82\,c{{m}^{2}}\]
CIRCUMFERENCE AND AREA OF A CIRCLE:
The distance around a circle is called the circumference of circle.
Circumference\[=2\pi r.\]
Example: Find the circumference of a circle when radius is 14 cm. \[\left( \pi =3\frac{1}{7} \right)\]
Solution: Circumference\[=2\pi r\]
\[=2\times 3\frac{1}{7}\times 14\]
\[=2\times \frac{22}{7}\times 14\]
\[=88\,cm.\]
Example: How many times will the wheel of a car rotate in a journey of 66 km if the diameter of wheel is 50cm?
Solution: Diameter of wheel (D) = 50 cm,
\[r=\frac{D}{2}=\frac{50}{2}=25\,cm\]
\[\therefore \] Circumference of the wheel\[=2\pi r\]
\[=2\pi \times 50\]
\[=100\pi \frac{22}{7}\]
\[=\frac{2200}{7}=314.28\,cm.\]
Length of journey\[=66\,km=66\times 1000\times 100\,cm.\]
\[=6600000\text{ }cms.\]
No. of times wheel will rotate to cover the journey
\[=\frac{\text{Length of journey}}{\text{Circumference of wheel}}\] \[=\frac{6600000}{314.28}=21000\]
AREA OF A CIRCLE:
Area of circle \[=\pi {{r}^{2}}\](r = radius)
Example: Find the area of circle when radius is 7 cm.
Solution: Area of circle\[=\pi {{r}^{2}}=\frac{22}{7}\times 7\times 7=154\,c{{m}^{2}}\]
AREA BETWEEN TWO CONCENTRIC CIRCLES:
If two concentric circles are there with radius R and r

Area between the circles = Area of outer circle area of inner circle
\[=\pi {{R}^{2}}-\pi {{r}^{2}}=\pi ({{R}^{2}}-{{r}^{2}})=\pi \,(R+r)\,(R-r)\]
Example: A 7 cm wide path is to be constructed all around, and outside a circular garden of diameter 112m.
Find the cost of constructing the path at Rs. 10/square. meter.
Solution: Radius of inner circle\[=\frac{112}{2}=56\,cm.\]
Radius of outer circle\[=\frac{112+7+7}{2}\]
\[=\frac{126}{2}=63\,m.\]
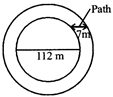
Area of path = Area of outer circle\[-\]Area of inner circle
\[=\pi {{63}^{2}}-\pi {{56}^{2}}\]
\[=\pi (63+56)\,(63-56)\]
\[=\pi \times 119\times 7\]
\[=\frac{22}{7}\times 119\times 7\]
\[=2618\,{{m}^{2}}\]
Cost of constructing path\[=10\times 2618=Rs.\,26180\]
QUADRILATERAL
Quadrilateral ABCD is shown in the following figure. Its diagonal BD divides it’s into two triangles. AL and CN are perpendicular to BD from A and C respectively.
Area (A) of quadrilateral ABCD is given by:
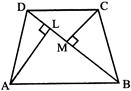
A = (area of\[\Delta ABD\]) + (area of\[\Delta BCD\])
\[=\left( \frac{1}{2}\times BD\times AL \right)+\left( \frac{1}{2}\times BD\times CM \right)\]
\[=\frac{1}{2}\times BD\times (AL+CM)\]
RHOMBUS
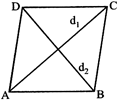
Where \[{{d}_{1}}\] and \[{{d}_{2}}\] are the measurements of the diagonals.
TRAPEZIUM
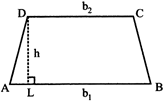 ·
·
\[=\frac{1}{2}\](sum of parallel sides)\[\times \]height
\[=\frac{1}{2}({{b}_{1}}+{{b}_{2}})h\]
CUBE
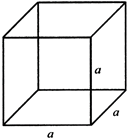
CUBOID
Let \[l,\text{b,h}\] are the edges of the cuboid, then,
Volume of cuboid\[=l\text{bh}\]cubic unit
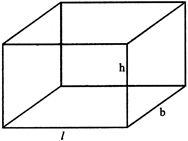
\[=2(lb+bh+hl)\]sq. unit
You need to login to perform this action.
You will be redirected in
3 sec
