9th Class Mathematics Coordinate Geometry Co-ordinate Geometry

       Introduction

In Euclidean geometry/we have studied about point lines etc. It is studied as independently. In 1637 Rene Wescartes firstly introduce the use of algebra in the study of geometry. This new type of geometry was further named as coordinate geometry. In this chapter we will study about coordinate geometry.  

       Co-ordinate Geometry

It is the branch of mathematics in which we solve geometrical problems with the help of algebra. To solve geometrical problem by this method need coordinate system.  

                Cartesian coordinate system

Suppose X'OX and Y'OY be two mutually perpendicular lines through any point "O". The point O is known as origin. Taking a convenient unit of length and starting from the origin mark off a number scale on horizontal as well vertical line. The line X'OX is known as X - axis and the line Y'OY is known as Y - axis.

If we are taking two lines together then it is known as coordinate axis.

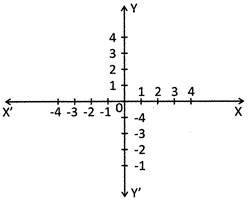
The coordinate of a point in Cartesian coordinate system is always written as ordered pair.\[(x,y)\]

i.e. \[(a,b)\ne (b,a)\]

The x - coordinate of a point is known as abscissa and y - coordinate is known as ordinate.

For a point (2, 4), 2 is abscissa and 4 is the ordinate.  

            Quadrants

Let X'OX and Y'OY are the coordinate axis and it divides Euclidean plane into four plane region. Every region is known as quadrants. So there are four quadrant for certesian plane which is shown below.

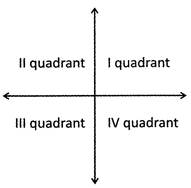
In I quadrant, \[x>0\] and \[\text{y}>0\]

In II quadrant, \[x>0\] and \[\text{y}>0\]

In III quadrant, \[x>0\] and \[\text{y}<0\]

In IV quadrant, \[x>0\] and \[\text{y}<0\]  

Write the quadrants of points in which they lie.

(a) (2, 3)                                              

(b) (-4, 3)

(c) (-5, -2)                                           

(d) (5, 2)

(e) None of these

Solution:

(a) (2, 3), Here, \[x>0\] and Y > 0, therefore, it lies I quadrant

(b) (- 4, 3), Here, \[x<0\] and y > 0, therefore, it lies II quadrant

(c) (- 5, - 2), Here, \[x<0\] and y < 0, therefore, it lies in III quadrant

(d) (5,-2), Here, \[x>0\] and y < 0, therefore, it lies in IV quadrant  

            Important Terms

(i) Point lies in the first quadrant if \[x>0\], y > 0

(ii) Point lies in the second quadrant if \[x<0\], y > 0

(iii) Point lies in the third quadrant if \[x<0\], y < 0

(iv) Point lies in the fourth quadrant if \[x>0\], y < 0

(v) Point lies on x - axis if y = 0

(vi) Point lies on y - axis if \[x=0\]

(vii) The coordinate of origin is (0, 0)