JEE Main & Advanced Mathematics Linear Programming Question Bank

Self Evaluation Test - Linear Programming Total Questions - 40

1)

The Solution set of constraints \[x+2y\ge 11,\]\[3x+4y\le 30,\]\[2x+5y\le 30\] and \[x\ge 0,\]\[y\ge 0,\] includes the point

A)
(2, 3)

B)
(3, 2)

C)
(3, 4)

D)
(4, 3)
View Solution
2)

Corner points of the feasible region for an LPP are\[(0,2)\]\[(3,0)\]\[(6,0)\],\[(6,8)\] and \[(0,5)\].Let \[F=4x+6y\] be the objective function. The minimum value of F occurs at

A)
\[(0,2)\] Only

B)
\[(3,0)\] Only

C)
The mind-point of the line segment joining the points \[(0,2)\] and \[(3,\,\,2)\]only

D)
Any point on the line segment joining the points \[(0,2)\] and \[(3,0)\]
View Solution
3)

The solution set of the following system of in equations: \[x+2y\le 3,\] \[3x+4y\ge 12,\]\[x\ge 0,\]\[y\ge 1,\] is

A)
Bounded region

B)
Unbounded region

C)
Only one point

D)
Empty set
View Solution
4)

Every gram of wheat provides 0.1 g of proteins and 0.25g of carbohydrates. The corresponding values of rice are 0.05 g and 0.5 g respectively. Wheat costs Rs. 4 per kg and rice Rs. 6. The minimum daily requirements of proteins and carbohydrates for an average child are 50 g and 200 g respectively. Then in what quantities should wheat and rice be mixed in the daily diet to provide minimum daily requirement of proteins and carbohydrates at minimum cost

A)
400, 200

B)
300, 400

C)
200, 400

D)
400, 300
View Solution
5)

The solution of linear programming problem maximize \[z=3{{x}_{1}}+5{{x}_{2}}\] Subject to \[3{{x}_{1}}+2{{x}_{2}}\le 18,\]\[{{x}_{1}}\le 4,{{x}_{2}}\le 6,{{x}_{1}}\ge 0,{{x}_{2}}\ge 0\] is

A)
\[{{x}_{1}}=2,{{x}_{2}}=0,z=6\]

B)
\[{{x}_{1}}=2,{{x}_{2}}=6,z=36\]

C)
\[{{x}_{1}}=4,{{x}_{2}}=3,z=27\]

D)
\[{{x}_{1}}=4,{{x}_{2}}=6,z=42\]
View Solution
6)

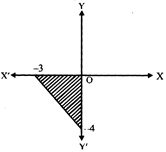
The feasible region for an LPP is shown shaded in the figure. Let \[Z=3x-4y\] be the objective function. Minimum of Z occurs at

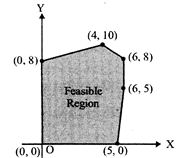
A)
(0, 0)

B)
(0, 8)

C)
(5, 0)

D)
(4, 10)
View Solution
7)

The maximum value of \[z=3x+4y\] subject to the condition \[x+y\le 40,x+2y\le 60,x,y\ge 0\] is

A)
130

B)
120

C)
40

D)
140
View Solution
8)

Consider \[\frac{x}{2}+\frac{y}{4}\ge 1\] and \[\frac{x}{3}+\frac{y}{2}\le 1,x,y\ge 0.\] Then number of possible solutions are:

A)
Zero

B)
Unique

C)
Infinite

D)
None of these
View Solution
9)

A shop-keeper deals in the sale of TV s and VCPs. He has 5.2 lacs to invest. He has only space for 50 pieces. ATV costs 20,000/- and a VCP costs 8,000/- From a TV and VCP he earns a profit of 1500/- and 800/- respectively. Assuming that he sells all the items that he purchases, the number of TVs and VCPs he should buy in order to Maximize his profit, is equal to

A)
60, 000

B)
55, 000

C)
51, 000

D)
47, 000
View Solution
10)

The maximum value of \[z=4x+3y\] subject to the constraints \[3x+2y\ge 160,5x+2y\ge 200,x+2y\ge 80,\]\[x,y\ge 0\] is.

A)
320

B)
300

C)
230

D)
None
View Solution
11)

The constraints\[-{{x}_{1}}+{{x}_{2}}\le 1,-{{x}_{1}}+3{{x}_{2}}\le 9,{{x}_{1}},{{x}_{2}}\ge 0\] Define on

A)
Bounded feasible space

B)
Unbounded feasible space

C)
Both bounded and unbounded feasible space

D)
None of these
View Solution
12)

A company manufactures two types of products A and B. The storage capacity of its go down is 100 units. Total investment amount is 30,000. The cost price of A and B are 400 and 900 respectively. Suppose all the product have sold and per unit profit is 100 and 120 through A and B respectively. If X units of A and Y units of B be produced, then two linear constraints and is profit line are respectively

A)
\[x+y=100;4x+9y=300,100x+120y=c\]

B)
\[x+y\le 100;4x+9y\le 300,x+2y=c\]

C)
\[x+y\le 100;4x+9y\le 300,100x+120y=c\]

D)
\[x+y\le 100;9x+4y\le 300,x+2y=c\]
View Solution
13)

Graph of the constrains \[\frac{x}{3}+\frac{y}{4}\le 1,x\ge 0,y\ge 0\] is

A)

B)

C)

D)

View Solution
14)

Consider the objective function \[Z=40x+50y.\] The minimum number of constraints that are required to maximize Z are

A)
4

B)
2

C)
3

D)
1
View Solution
15)

Maximize \[Z=3x+5y,\] subject to \[x+4y\le 24,\]\[3x+y\le 21,\]\[x+y,\le 9,\]\[x\ge 0,y\ge 0,\] is

A)
\[20\,at\,(1,0)\]

B)
\[30\,\,at\,\,(0,6)\]

C)
\[37\,at\,(4,5)\]

D)
\[33\,\,at\,\,(6,3)\]
View Solution
16)

The maximum value of \[z=4x+2y\]subject to constraints \[2x+3y\le 18,x+y\ge 10\] and \[x,y\ge 0\], is

A)
36

B)
40

C)
20

D)
None of these
View Solution
17)

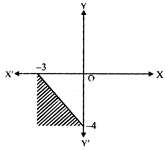
Feasible region for an LPP is shown shaded in the following figure. Minimum of \[Z=4x+3y\]occurs at the point.

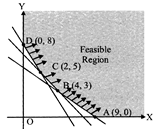
A)
(0, 8)

B)
(2, 5)

C)
(4, 3)

D)
(9, 0)
View Solution
18)

A wholesale merchant wants to start the business of cereal with 24000. Wheat is 4000 per quintal and rice is 600 per quintal. He has capacity to store 200 quintal cereal. He earns the profit 25 per quintal on wheat and 40 per quintal on rice. If he store x quintal rice and y quintal wheat then for maximum profit, the objective function is

A)
\[25x+40y\]

B)
\[40x+25y\]

C)
\[400x+600y\]

D)
\[\frac{400}{40}x+\frac{600}{25}y\]
View Solution
19)

Which of the following is not a vertex of the positive region bounded by the inequalities \[2x+3y\le 6,5x+3y\le 15\] and \[x,y\ge 0\]

A)
(0, 2)

B)
(0, 0)

C)
(3, 0)

D)
All of these
View Solution
20)

The maximum value \[z=5x+2y,\]subject to the constraints \[x+y\le 7,x+2y\le 10,x,y\ge 0\]is

A)
10

B)
26

C)
35

D)
70
View Solution
21)

For the constraint of a linear optimizing function\[z={{x}_{1}}+{{x}_{2}},\] Given by \[{{x}_{1}}+{{x}_{2}}\le 1,3{{x}_{1}}+{{x}_{2}}\ge 3\]and\[{{x}_{1}},{{x}_{2}}\ge 0\].

A)
There are two feasible regions

B)
There are infinite feasible regions

C)
There is no feasible region

D)
None of these
View Solution
22)

The maximum value of \[z=2x+5y\] subject to the constraints \[2x+5y\le 10,x+2y\ge 1,x-y\le 4,x\ge y\ge 0,\] Occurs at

A)
Exactly one pint

B)
Exactly two points

C)
Infinitely many points

D)
None of these
View Solution
23)

An oil company required 12000, 20000 and 15000 barrels of high-grade, medium grade and low grade oil, respectively. Refinery A produces 100, 300 and 200 barrels per day of high-grade, medium-grade and low-grade oil, respectively, while refinery B produces 200, 400 and 100 barrels per day of high-grade. Medium-grade and low grade oil, respectively. If refinery A costs 400 per day and refinery B costs 300 per day to operate, then the days should each he run to minimize costs while satisfying requirements are

A)
30, 60

B)
60, 30

C)
40, 60

D)
60, 40
View Solution
24)

A vertex of bounded region of inequalities \[x\ge 0\]\[x+2y\ge 0\] and \[2x+y\le 4\]is

A)
(1, 1)

B)
(0, 1)

C)
(3, 0)

D)
(0, 4)
View Solution
25)

Which of these terms is not used in a linear programming problem?

A)
Slack variables

B)
Objective function

C)
Concave region

D)
Feasible solution
View Solution
26)

The maximum value of \[z=6x+8y\] subject to constraints \[2x+y\le 30,x+2y\le 24\] and \[x\ge 0,y\ge 0\] is

A)
90

B)
120

C)
96

D)
240
View Solution
27)

Consider: \[z=3x+2y\] Minimize subject to:\[x+y\ge 8\]\[3x+5y\le 15\]\[x,y\ge 0\] It has:

A)
Infinite feasible solutions

B)
Unique feasible solution

C)
No feasible solution

D)
None of these
View Solution
28)

The number of corner points of the L.P.P. Max \[Z=20x+3y\] subject to the constraints \[x+y\le 5,2x+3y\le 12,x\ge 0,y\ge 0\] are

A)
4

B)
3

C)
2

D)
1
View Solution
29)

The maximum value of \[z=3x+2y,\]subjected to the conditions \[x+2y\ge 2,x+2y\le 8,x,y\ge 0\] is

A)
32

B)
24

C)
40

D)
None of these
View Solution
30)

The Maximum value of \[z=5x+3y\], subjected to the conditions\[3x+5y\le 15,5x+2y\le 10,x,y\ge 0\]is

A)
\[\frac{235}{19}\]

B)
\[\frac{325}{19}\]

C)
\[\frac{523}{19}\]

D)
\[\frac{532}{19}\]
View Solution
31)

The constraints \[-{{x}_{1}}+{{x}_{2}}\le 1,-{{x}_{1}}+3{{x}_{2}}\le 9;\]\[{{x}_{1}},{{x}_{2}}\ge 0\] defines on

A)
Bounded feasible space

B)
Unbounded feasible space

C)
Both bounded and unbounded feasible space

D)
None of these
View Solution
32)

A brick manufacture has two depots A and B, with stocks of 30000 and 20000 bricks respectively. He receive orders form three builders P, Q and R for 15000, 20,000 and 15000 bricks respectively. The cost (in) of transporting 1000 bricks to the builders form the deposits as given in the table.

To From Transportation cost per 1000 bricks (in Rs.)

P Q R

A 40 20 20

B 20 60 40

The manufacturer wished to find how to fulfill the order so that transportation cost is minimum. Formulation of the L.P.P., is given as

A)
Minimize \[Z=40x-20y\] Subject to, \[x+y\ge 15,x+y\le 30,x\ge 15,y\le 20,\]\[x\ge 0,y\ge 0\]

B)
Minimize \[Z=40x-20y\] Subject to, \[x+y\ge 15,x+y\le 30,x\le 15,y\ge 20,\]\[x\ge 0,y\ge 0\]

C)
Minimize \[Z=40x-20y\] Subject to, \[x+y\ge 15,x+y\le 30,x\le 15,y\le 20,\]\[x\ge 0,y\ge 0\]

D)
Minimize \[Z=40x-20y\] Subject to, \[x\ge 0,y\ge 0\]
View Solution
33)

The inequalities \[5x+4y\ge 20,x\le 6,y\le 4\]from

A)
A square

B)
A rhombus

C)
A triangle

D)
A quadrilateral
View Solution
34)

Maximize \[Z=4x+6y,\] subject to \[3x+2y\le 12,\]\[x+y\ge 4,x,y\ge 0,\]is

A)
\[16\,\,at\,(4,0)\]

B)
\[24\,\,at\,\,(0,4)\]

C)
\[24\,\,at\,(6,0)\]

D)
\[36\,\,at\,(0,6)\]
View Solution
35)

In equations \[3x-y\ge 3\] and \[4x-y\ge 4\]

A)
Have solution for positive x and y

B)
Have no solution for positive x and y

C)
Have solution for all x

D)
Have solution for all y
View Solution
36)

\[Z=7x+y,\] subject to\[5x+y\ge 5,x+y\ge 3,x\ge 0,y\ge 0.\] The minimum value of Z occurs at

A)
(3, 0)

B)
\[\left( \frac{1}{2},\frac{5}{2} \right)\]

C)
(7, 0)

D)
(0, 5)
View Solution
37)

The true statement for the graph of in equations\[3x+2y\le 6\] and \[6x+4y\ge 20,\] is

A)
Both graph are disjoint

B)
Both contain (0, 3)

C)
Both contain point (1, 1)

D)
None of these
View Solution
38)

Shamli wants to invest 50,000 in saving certificates and PPF. She wants to invest at least 15,000 in saving certificate and at least 20, 000 in PPF. The rate of interest on saving certificates is \[8%P.a.\]and that on PPF is 9% P. a formulation of the above problem as LPP to determine maximum Yearly income, is

A)
Maximize \[Z=0.08x+0.09y\] subject to, \[x+y\le 50,000,x\ge 15000,\]

B)
Maximize \[Z=0.08x+0.09y\] subject o, \[x+y\le 50,000,x\ge 15000,y\le 20,000\]

C)
Maximize \[Z=0.08x+0.09y\]subject to, \[x+y\le 50,000,x\le 15000,y\ge 20,000\]

D)
Maximize \[Z=0.08x+0.09y\] subject to, \[x+y\le 50,000,x\le 15000,y\le 20,000\]
View Solution
39)

The maximum value of \[P=x+3y\] such that \[2x+y\le 20,x+2y\le 20,x\ge 0,y\ge 0\] is

A)
10

B)
60

C)
30

D)
None of these
View Solution
40)

A printing company prints two types of magazines A and B. The company earns 10 and 15 on each magazine A and B respectively. These are processed on three machines I, II & III and total time in hours available per week on each machine is as follows:

Magazine \[\to \] A(x) B(y) Time available

\[\downarrow \]Machine

I 2 3 36

II 5 2 50

III 2 6 60

The number of constraints is

A)
3

B)
4

C)
5

D)
6
View Solution

Study Package

Self Evaluation Test - Linear Programming

Buy Now

To From	Transportation cost per 1000 bricks (in Rs.)
To From	P	Q	R
A	40	20	20
B	20	60	40

Magazine \[\to \]	A(x)	B(y)	Time available
\[\downarrow \]Machine
I	2	3	36
II	5	2	50
III	2	6	60

JEE Main & Advanced Mathematics Linear Programming Question Bank

done Self Evaluation Test - Linear Programming Total Questions - 40

Study Package

Self Evaluation Test - Linear Programming

Self Evaluation Test - Linear Programming Total Questions - 40