-
question_answer1) If the quadratic equation \[p{{x}^{2}}-2\sqrt{5}\,px+15=0,\] has two equal roots then find the value of p.
View Answer play_arrow
-
question_answer2)
| In figure 1, a tower AB is 20 m high and BC, its shadow on the ground, is \[20\sqrt{3}\,m\] long. Find the sun's altitude. |
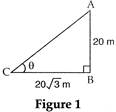 |
View Answer play_arrow
-
question_answer3) Two different dice are tossed together. Find the probability that the product of two numbers on the top of the dice is 6.
View Answer play_arrow
-
question_answer4)
| In figure 2, PQ is a chord of a, circle with centre O and PT is a tangent If \[\angle QPT=60{}^\circ \], find \[\angle PRQ\]. |
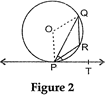 |
View Answer play_arrow
-
question_answer5)
| In figure 3, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If \[\angle PRQ=120{}^\circ \], then prove that, \[OR=PR+RQ\]. |
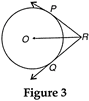 |
View Answer play_arrow
-
question_answer6)
| In figure 4, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of \[\Delta \,ABC\] is \[54\text{ }c{{m}^{2}}\], then find the lengths of sides AB and AC. |
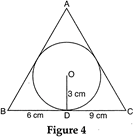 |
View Answer play_arrow
-
question_answer7) Solve the following quadratic equation for x: \[4{{x}^{2}}+4bx-\left( {{a}^{2}}-{{b}^{2}} \right)=0\]
View Answer play_arrow
-
question_answer8) In an A.P., if \[~{{S}_{5}}+{{S}_{7}}=167\] and \[{{S}_{10}}=235\], find the A.P. where \[{{S}_{n}}\] denotes the sum of its first n terms.
View Answer play_arrow
-
question_answer9) The points \[A(4,7),\,\,B(p,3)\] and \[C(7,3)\] are the vertices of a right triangle, right-angled at B. Find the value of p.
View Answer play_arrow
-
question_answer10) Find the relation between x and y if the points \[A(x,y),\,B(-5,7)\] and \[C(-4,5)\]are collinear.
View Answer play_arrow
-
question_answer11) The 14th term of an AP is twice its 8th term. If its 6th term is\[8\], then find the sum of its first 20 terms.
View Answer play_arrow
-
question_answer12) Solve for x: \[\sqrt{3}{{x}^{2}}-2\sqrt{2}x-2\sqrt{3}=0\]
View Answer play_arrow
-
question_answer13) The angle of elevation of an aeroplane from point A on the ground is \[60{}^\circ \]. After flight of 15 seconds, the angle of elevation change to \[30{}^\circ \]. If the aeroplane is flying at a constant height of \[1500\sqrt{3}\,m\], find the speed of the plane in km/hr.
View Answer play_arrow
-
question_answer14) If the coordinates of points A and B are \[(-2,-2)\] and \[(2,-4)\] respectively find the coordinates of P such that \[AP=\frac{3}{7}AB,\]where P lies on the line segment AB.
View Answer play_arrow
-
question_answer15) A probability of selecting a red ball at random from a jar that contains only red, blue and orange is \[\frac{1}{4}\]. The probability of selecting a blue ball at random from the same jar is \[\frac{1}{3}\]. If the jar contains 10 orange balls, find the total number of balls in the jar.
View Answer play_arrow
-
question_answer16) Find the area of the minor segment of a circle of radius 14 cm, when its central angle is \[60{}^\circ \]. Also find the area of the corresponding major segment. [Use \[\pi =\frac{22}{7}\]]
View Answer play_arrow
-
question_answer17) Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m and the canvas to be used costs Rs. 100 per sq. m. Find amount the associations will have to pay. What values are shown by these associations?
View Answer play_arrow
-
question_answer18) A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
View Answer play_arrow
-
question_answer19) A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm [Use\[\pi =3.14\]]
View Answer play_arrow
-
question_answer20) 504 cones each of diameter 3.5 cm and height 3 cm. are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area. \[\left[ \pi =\frac{22}{7} \right]\]
View Answer play_arrow
-
question_answer21) The diagonal of a rectangular field is 16 m more than the shorter side. If the longer side is 14 m more than the shorter side, then find the lengths of the sides of the field.
View Answer play_arrow
-
question_answer22) Find the 60th term of the A.P. 8, 10, 12.... if it has a total of 60 terms and hence find the sum of its last 10 terms.
View Answer play_arrow
-
question_answer23) A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
View Answer play_arrow
-
question_answer24) Prove that the lengths of the tangents drawn from an external point to a circle are equal.
View Answer play_arrow
-
question_answer25) Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
View Answer play_arrow
-
question_answer26) Construct a \[\Delta \text{ }ABC\] in which \[AB=6\text{ }cm,\text{ }\angle A=30{}^\circ \] and \[\angle B=60{}^\circ \]. Construct another \[\Delta \text{ }AB'C\]similar to \[\Delta \text{ }ABC\]with base\[AB'=8\text{ }cm\].
View Answer play_arrow
-
question_answer27) At a point A, 20 m above the level of water in a lake, the angle of elevation of a cloud is \[30{}^\circ \]. The angle of depression of the reflection of the cloud in the lake, at A is \[60{}^\circ \]. Find the distance of the cloud from A.
View Answer play_arrow
-
question_answer28)
| A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is |
| (i) A card of spade or an ace |
| (ii) A black king |
| (iii) Neither a jack nor a king |
| (iv) Either a king or a queen |
View Answer play_arrow
-
question_answer29) Find the values of k so that the area of the triangle with vertices \[(1,-1),\,\,(-4,2k)\] and \[(-k,-5)\] is 24 sq. units.
View Answer play_arrow
-
question_answer30)
| In figure 5, PQRS is a square lawn with side \[PQ=42\text{ }m\]. Two circular flower beds are there on the sides PS and QR with center at O, the intersection of its diagonals. Find the total area of the two flower beds (shaded parts). |
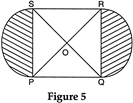 |
View Answer play_arrow
-
question_answer31) From each end of a solid metal cylinder, metal was scooped out in hemispherical form of same diameter. The height of the cylinder is 10 cm and its base is of radius 4.2 cm. The rest of the cylinder is melted and converted into a cylindrical wire of 1.4 cm thickness. Find the length of the wire.
View Answer play_arrow





