-
question_answer1)
The area of a rhombus, one side of which measures 25 cm and diagonal 30 cm, is
A)
600 sq cm done
clear
B)
250 sq cm done
clear
C)
200 sq cm done
clear
D)
150 sq cm done
clear
View Solution play_arrow
-
question_answer2)
The cross-section of a canal is a trapezium in shape. If the can I is 8m wide at the top and 6 m wide at the bottom and the area of cross-section is 644 sq m, then the length of the canal is
A)
90 m done
clear
B)
92 m done
clear
C)
94 m done
clear
D)
96 m done
clear
View Solution play_arrow
-
question_answer3)
If BC passes through the centre of the circle, then the area of the shaded region in the given figure is
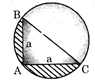
A)
\[\frac{{{a}^{2}}}{2}(3-\pi )\] done
clear
B)
\[\frac{{{a}^{2}}}{2}\left( \frac{\pi }{2}-1 \right)\] done
clear
C)
\[2{{a}^{2}}(\pi -1)\] done
clear
D)
\[\frac{{{a}^{2}}}{2}\left( \frac{\pi }{2}-1 \right)\] done
clear
View Solution play_arrow
-
question_answer4)
The area (in square units) of a regular hexagon, each side of which is 2 units, is
A)
8 done
clear
B)
10.392 (approx) done
clear
C)
12.5 done
clear
D)
18 done
clear
View Solution play_arrow
-
question_answer5)
The sides of an equilateral triangle are \[\left( \text{2a}-\text{b} \right)\] cm, \[\left( \text{a}+\text{3b} \right)\]cm and \[\left( \text{2a}-\text{2b}+\text{1} \right)\] cm, then the perimeter of the triangle is
A)
3 cm done
clear
B)
12cm done
clear
C)
15cm done
clear
D)
21cm done
clear
View Solution play_arrow
-
question_answer6)
One side of a parallelogram is 8 cm. If the corresponding altitude is 6 cm, then its area is given by
A)
\[\text{24 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{36 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{4}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{48 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer7)
The sides of a triangle are 5 cm, 12 cm and 13 cm. Then its area is
A)
\[0.00\text{24 }{{\text{m}}^{\text{2}}}\] done
clear
B)
\[0.00\text{26 }{{\text{m}}^{\text{2}}}\] done
clear
C)
\[0.00\text{3}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[0.00\text{15}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer8)
The area of a right angled triangle is \[\text{2}0\text{ c}{{\text{m}}^{\text{2}}}\]and one of the sides containing the right triangle is 4 cm. Then the altitude on hypotenuse is
A)
8 cm done
clear
B)
10 cm done
clear
C)
\[\frac{10}{\sqrt{41}}cm\]cm done
clear
D)
\[\frac{20}{\sqrt{29}}cm\] done
clear
View Solution play_arrow
-
question_answer9)
The area of a triangle, whose sides are 4 cm, 13 cm and 15 cm, is
A)
\[\sqrt{\text{4}.\text{2}0}\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{24 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{48 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{56 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer10)
If the sides of a triangle are doubled, then its area
A)
remains the same done
clear
B)
becomes doubled done
clear
C)
becomes three times done
clear
D)
becomes four times done
clear
View Solution play_arrow
-
question_answer11)
The base of a triangle is 15 dm and its height is 12 dm. The height of another triangle of double the area and the base of which is 20 dm, is given by
A)
9 dm done
clear
B)
18 dm done
clear
C)
8 dm done
clear
D)
12.5 dm done
clear
View Solution play_arrow
-
question_answer12)
In aright triangle with sides\[x\] and y, hypotenuse z, the altitude drawn on the hypotenuse is a, then
A)
\[xy={{a}^{2}}\] done
clear
B)
\[\frac{1}{x}+\frac{1}{y}=\frac{1}{a}\] done
clear
C)
\[{{x}^{2}}+{{y}^{2}}=2{{a}^{2}}\] done
clear
D)
\[\frac{1}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}=\frac{1}{{{a}^{2}}}\] done
clear
View Solution play_arrow
-
question_answer13)
The diagonal of a square A is\[(x+y)\]. The diagonal of square B with twice the area of A is
A)
\[\sqrt{2}(x+y)\] done
clear
B)
\[2(x+y)\] done
clear
C)
\[2x+2y\] done
clear
D)
\[4x+2y\] done
clear
View Solution play_arrow
-
question_answer14)
A circle and a square have the same perimeter. Then
A)
Their areas are equal done
clear
B)
The area of the circle is greater done
clear
C)
The area of the square is greater done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer15)
Squares are constructed on the outer side of a right-angled triangle on each of its three sides. If the lengths of the two sides containing the right angle are 5 cm and 10 cm respectively, then the total area of the regions bounded by the diagram is
A)
250 sq cm done
clear
B)
200 sq cm done
clear
C)
300 sq cm done
clear
D)
275 sq cm done
clear
View Solution play_arrow
-
question_answer16)
The area of the field ABDFEA is
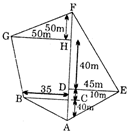
A)
\[\text{7225 }{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{723}0\text{ }{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{7235 }{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{724}0{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer17)
The total surface area of the cube is 216 sq. cm. The length of the longest pole that can be kept inside the cube is
A)
\[6\sqrt{3}\] done
clear
B)
6 done
clear
C)
8 done
clear
D)
\[7\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer18)
The dimensions of a hall are 40 m, 25 m and 20 m. If each person requires 200 cubic m, then the number of persons who can be accommodated in the hall are
A)
150 done
clear
B)
140 done
clear
C)
120 done
clear
D)
100 done
clear
View Solution play_arrow
-
question_answer19)
The lengths of the sides of a triangle are in integers and its area is also an integer. One side is 21 cm and the perimeter is 48 cm, then the length of the shortest side is
A)
8 cm done
clear
B)
10 cm done
clear
C)
12 cm done
clear
D)
14 cm done
clear
View Solution play_arrow
-
question_answer20)
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is \[6\sqrt{2}\] cm, then the area of the triangle is
A)
\[16\sqrt{2}c{{m}^{2}}\] done
clear
B)
\[16\sqrt{3}c{{m}^{2}}\] done
clear
C)
\[12\sqrt{2}c{{m}^{2}}\] done
clear
D)
\[12\sqrt{3}c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer21)
The diagonals of a rhombus are 8 cm and 10 cm. Then the area of the rhombus is
A)
\[\text{64 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{1}00\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{8}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{4}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer22)
If the diagonals of a rhombus are 24 dm and 10 dm, then the perimeter of the rhombus will be
A)
68 dm done
clear
B)
60 dm done
clear
C)
52 dm done
clear
D)
50 dm done
clear
View Solution play_arrow
-
question_answer23)
A 2 unit high marble slab with a 1 unit x 4 unit base is fixed to the floor of a courtyard. The surface area of the marble which is visible is
A)
28 sq. units done
clear
B)
36 sq. units done
clear
C)
24 sq. units done
clear
D)
20 sq. units done
clear
View Solution play_arrow
-
question_answer24)
A river 3 m deep and 60 m wide is flowing at t rate of 2.4 km/hour. The amount of water running into the sea per minute is
A)
6000 cubic m done
clear
B)
6400 cubic m done
clear
C)
6800 cubic m done
clear
D)
7200 cubic m done
clear
View Solution play_arrow
-
question_answer25)
The height of a conical tent at the centre is 5 r The distance of any point on its circular base from the top of the tent is 13 m. The area of the slant surface is
A)
144 \[\pi \] sq m done
clear
B)
130 \[\pi \] sq m done
clear
C)
156 \[\pi \] sq m done
clear
D)
169 \[\pi \] sq m done
clear
View Solution play_arrow
-
question_answer26)
The area of the curved surface of a right circular cone of diameter 14 cm is \[\text{55}0\text{ c}{{\text{m}}^{\text{2}}}\] The height of the cone is
A)
25 cm done
clear
B)
22 cm done
clear
C)
23 cm done
clear
D)
24 cm done
clear
View Solution play_arrow
-
question_answer27)
A right pyramid is on a regular hexagonal base. Each side of the base is 10 m. Its height is 60 m. The volume of the pyramid is
A)
\[\text{5196}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{52}00{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{521}0\text{ }{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{522}0\text{ }{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer28)
A cone whose height is 15 cm and radius of base is 6 cm, is trimmed sufficiently to reduce it to a pyramid whose base is an equilateral triangle. The volume of the portion of removed is
A)
\[\text{325 c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{328 c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{33}0\text{ c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{332 c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer29)
The area of a parallelogram is 70 dm2 and its altitude is 7 dm, then the perimeter of a rectangle of equal area standing on the same base is
A)
40 dm done
clear
B)
28 dm done
clear
C)
34 dm done
clear
D)
17 dm done
clear
View Solution play_arrow
-
question_answer30)
The perimeter of a rhombus is 100 cm and one of the diagonals is 40 cm. Then the area of the rhombus is
A)
\[\text{1}000\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{5}00\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{12}00\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{6}00\text{c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer31)
If the radius of the circle is increased by 100%,then the area is increased by
A)
100% done
clear
B)
200% done
clear
C)
300% done
clear
D)
400% done
clear
View Solution play_arrow
-
question_answer32)
The radius of a circle is increased by 1 cm, then the ratio of the new circumference to the new diameter is
A)
\[\pi +2\] done
clear
B)
\[\pi +1\] done
clear
C)
\[\pi \] done
clear
D)
\[\pi -\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer33)
If the difference between the circumference and radius of a circle is 37 cm, then the area of the
A)
\[\text{111 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{148 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{259 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{154 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer34)
A square ABCD is inscribed in a circle of radius a. Another circle is inscribed in ABCD and a square EFGH is inscribed in this circle. The side EF is equal to
A)
a done
clear
B)
\[a\sqrt{2}\] done
clear
C)
\[\frac{a}{\sqrt{2}}\] done
clear
D)
\[\frac{a}{2}\] done
clear
View Solution play_arrow
-
question_answer35)
Inside a triangular garden, there is a flower bed in the form of a similar triangle. Around the flower bed runs a uniform path of such a width that the sides of the garden are double of the corresponding sides of the flower bed. The areas of the path and the flower bed are in the ratio
A)
1 : 1 done
clear
B)
1 : 2 done
clear
C)
1 : 3 done
clear
D)
3 :1 done
clear
View Solution play_arrow
-
question_answer36)
If a solid right circular cylinder made of iron is heated to increase its radius and height by 1 p.c. each, then the volume of the solid is increased by
A)
1.01 p.c. done
clear
B)
3.03 p.c. done
clear
C)
2.01 p.c. done
clear
D)
1.2 p.c. done
clear
View Solution play_arrow
-
question_answer37)
If the volume and surface area of a sphere are numerically the same, then its diameter is
A)
6 units done
clear
B)
8 units done
clear
C)
10 units done
clear
D)
12 units done
clear
View Solution play_arrow
-
question_answer38)
The radius of a piece of wire is decreased to one-half. If volume remains the same, then its length will increase
A)
2 times done
clear
B)
3 times done
clear
C)
4 times done
clear
D)
5 times done
clear
View Solution play_arrow
-
question_answer39)
The side of a square is 2 cm and semicircles are constructed on each side of the square, then the area of the whole figure is
A)
\[\left( \text{4 }+\text{ 2}\pi \right)\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\left( \text{4 }+\text{ 4}\pi \right)\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{47}\pi \text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{87}\pi \text{ c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer40)
The area of a square that can be inscribed in a circle of radius r is
A)
\[{{\text{r}}^{\text{2}}}\] done
clear
B)
\[\text{2 }{{\text{r}}^{\text{2}}}\] done
clear
C)
\[\text{4 }{{\text{r}}^{\text{2}}}\] done
clear
D)
\[\pi \text{ }{{\text{r}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer41)
A rectangular sheet of cardboard is 4 cm by 2 cm. The greatest possible circle is cut off from the cardboard, then the remaining area is
A)
\[\left( \text{16}-\pi \right)\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\left( \text{16}-\text{4}\pi \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\left( \text{8}-\pi \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\left( \text{8}-\text{4}\pi \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer42)
A wire in the shape of an equilateral triangle encloses an area , s1 sq. cm. If the same wire is bent to form circle, the area of the circle will be
A)
\[\frac{\pi {{s}^{2}}}{9}\] done
clear
B)
\[\frac{3{{s}^{2}}}{\pi }\] done
clear
C)
\[\frac{3s}{\pi }\] done
clear
D)
\[\frac{3\sqrt{3s}}{\pi }\] done
clear
View Solution play_arrow
-
question_answer43)
A rectangular sheet of paper 22 cm long and 12 cm broad can be curved to form the lateral surface of a right circular cylinder in two ways. Taking \[\pi =\frac{22}{7}\], the difference between the volumes of the two cylinders thus formed is
A)
200 c.c. done
clear
B)
210 c.c. done
clear
C)
250 c.c. done
clear
D)
252 c.c. done
clear
View Solution play_arrow
-
question_answer44)
The length and breadth of a room are in the ratio of 3:2. Its height is equal to half of its length. If the cost of carpeting the floor at Rs. \[\text{4}.00\text{ per }{{\text{m}}^{\text{2}}}\]is Rs, 216, then the area of four walls (in\[{{\text{m}}^{\text{2}}}\]) is
A)
135 done
clear
B)
140 done
clear
C)
125 done
clear
D)
120 done
clear
View Solution play_arrow
-
question_answer45)
The area of the figure ABCDEFGA is
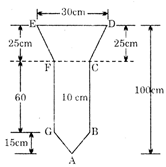
A)
\[\text{1175 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{1185 c}{{\text{m}}^{2}}\] done
clear
C)
\[\text{1195 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{1199 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer46)
Two circles, each of unit radius, are so drawn that the centre of each lies on the circumference of the other. The area of the region, common to both the circles, is
A)
\[\frac{(4\pi -3\sqrt{3})}{12}\] done
clear
B)
\[\frac{(4\pi -6\sqrt{3})}{12}\] done
clear
C)
\[\frac{(4\pi -3\sqrt{3})}{6}\] done
clear
D)
\[\frac{(4\pi -6\sqrt{3})}{6}\] done
clear
View Solution play_arrow
-
question_answer47)
The area of a field surveyed is 11,200 sq. m. The readings in the given field book are in meters. The value of \[x\] will be
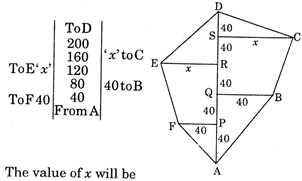
A)
20 m done
clear
B)
30 m done
clear
C)
40 m done
clear
D)
50 m done
clear
View Solution play_arrow
-
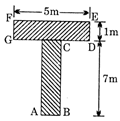
question_answer48)
Area of shaded portion as shown in the figure
A)
\[\text{12 }{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{13}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{14 }{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{15}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer49)
The circumference of a circle is 100 cm. Then the side of a square inscribed in the circle is
A)
\[\frac{100\sqrt{2}}{\pi }cm\] done
clear
B)
\[\frac{50\sqrt{2}}{\pi }cm\] done
clear
C)
\[\frac{100}{\pi }cm\] done
clear
D)
\[50\sqrt{2}\,cm\] done
clear
View Solution play_arrow
-
question_answer50)
A solid cylinder of glass whose diameter is 1.5 m and height 1 m is melted and turned into a sphere. The diameter of a sphere is
A)
1m done
clear
B)
0.75m done
clear
C)
1.25m done
clear
D)
1.5m done
clear
View Solution play_arrow
-
question_answer51)
A rectangle with one side equal to 4 cm is inscribed in a circle of diameter 5 cm. Then the area of the rectangle is
A)
\[\text{12 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{15 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{16 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[8\sqrt{2}c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer52)
The area of a circle inscribed in an equilateral triangle is 4870 square units. Then the perimeter of the triangle is (in units)
A)
\[72\sqrt{3}\] done
clear
B)
\[48\sqrt{3}\] done
clear
C)
72 done
clear
D)
36 done
clear
View Solution play_arrow
-
question_answer53)
A cuboid is such that its length is 2 times the width and the width is 2 times its height. The side of a square, whose area is equal to the total surface area of the cuboid, in terms of the height of the cuboid is
A)
\[4h\] done
clear
B)
\[6h\] done
clear
C)
\[2\sqrt{7}h\] done
clear
D)
\[4\sqrt{7}h\] done
clear
View Solution play_arrow
-
question_answer54)
The percentage increase in the surface area of a cube, when each side is increased to \[\frac{3}{2}\] times the original length is
A)
225 done
clear
B)
200 done
clear
C)
175 done
clear
D)
125 done
clear
View Solution play_arrow
-
question_answer55)
The dimensions of a hall are 50 m, 25 m and 9 m If each person required 150 cubic m, then the number of persons who can be accommodated in the hall are
A)
60 done
clear
B)
65 done
clear
C)
70 done
clear
D)
75 done
clear
View Solution play_arrow
-
question_answer56)
A tank 15 m long, 10 m wide and 6m deep is open at the top. If the width of the sheet is 2m then the cost of iron sheet at the rate of Rs. 5 per meter is
A)
Rs. 550 done
clear
B)
Rs. 1050 done
clear
C)
Rs. 1125 done
clear
D)
Rs. 1150 done
clear
View Solution play_arrow
-
question_answer57)
If the right circular cone is separated into three solids of volume \[{{\upsilon }_{1}},{{\upsilon }_{2}},{{\upsilon }_{3}}\] by two planes parallel to the base and trisect the altitude, then \[{{\upsilon }_{1}},{{\upsilon }_{2}},{{\upsilon }_{3}}\]is
A)
1: 2 : 3 done
clear
B)
1 : 4 : 6 done
clear
C)
1 : 6 : 9 done
clear
D)
1:7:19 done
clear
View Solution play_arrow
-
question_answer58)
Two cones A and B have their base radii in the ratio of 4 : 3 and their heights in the ratio 3:4. The ratio of volume of cone A to that of cone B is
A)
4: 3 done
clear
B)
3 : 4 done
clear
C)
2: 3 done
clear
D)
1 : 2 done
clear
View Solution play_arrow
-
question_answer59)
Water flows at the rate of 10 m per minute from a cylindrical pipe 5 mm in diameter. A conical vessel, whose diameter at the base is 40 cm and depth 24 cm, is filled. The time taken to fill the conical vessel is
A)
50 minutes done
clear
B)
50 minutes 12 seconds done
clear
C)
51 minutes 12 seconds done
clear
D)
51 minutes 15 seconds done
clear
View Solution play_arrow
-
question_answer60)
The volume of a right circular cone of height 10 cm and radius of base 6 cm is
A)
\[\text{6}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{9}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{12}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{18}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer61)
The area of the largest triangle that can be inscribed in a semi-circle whose radius is r cm is
A)
\[\text{2 r c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[{{\text{r}}^{\text{2}}}\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{2 }{{\text{r}}^{\text{2}}}\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{4 }{{\text{r}}^{\text{2}}}\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer62)
A cord in the form of a square encloses the area 'S'\[\text{c}{{\text{m}}^{\text{2}}}\]. If the same cord is bent into the form of a circle, then the area of the circle is
A)
\[\frac{\pi {{S}^{2}}}{4}\] done
clear
B)
\[4\,\pi \,{{S}^{2}}\] done
clear
C)
\[\frac{S}{4\pi }\] done
clear
D)
\[\frac{4S}{\pi }\] done
clear
View Solution play_arrow
-
question_answer63)
A circle is inscribed in an equilateral triangle and a square is inscribed in the circle, then the ratio of the area of the triangle to the area of the square is
A)
\[\sqrt{3}:\,1\] done
clear
B)
\[\sqrt{3}:\,\sqrt{2}\] done
clear
C)
\[3:\,\sqrt{2}\] done
clear
D)
\[3\sqrt{3}:\,2\] done
clear
View Solution play_arrow
-
question_answer64)
A circular disc of radius 10 cm is divided into sectors with angles \[120{}^\circ \] and \[150{}^\circ \], then the ratio of the area of two sectors is
A)
4: 5 done
clear
B)
5 : 4 done
clear
C)
2 : 1 done
clear
D)
8 : 7 done
clear
View Solution play_arrow
-
question_answer65)
A circular wire of radius 1 dm is cut and is placed along the circumference of a circle of radius of one metre. The angle subtended by the wire at the centre of the circle is equal to
A)
\[\frac{\pi }{4}\] radian done
clear
B)
\[\frac{\pi }{3}\] radian done
clear
C)
\[\frac{\pi }{5}\] radian done
clear
D)
\[\frac{\pi }{10}\]radian done
clear
View Solution play_arrow
-
question_answer66)
The ratio of the radii of two cylinders is \[1:\sqrt{3}\] and their heights are in the ratio 2 : 3 . The ratio of their volumes is
A)
1 : 9 done
clear
B)
2 : 9 done
clear
C)
4 : 9 done
clear
D)
5 : 9 done
clear
View Solution play_arrow
-
question_answer67)
A sphere of radius 4 cm has the same volume as that of a cone with a circular base of radius 4 cm. The height of the cone is
A)
12 cm done
clear
B)
16 cm done
clear
C)
20 cm done
clear
D)
24 cm done
clear
View Solution play_arrow
-
question_answer68)
The number of balls of radius 1 cm that can be made from a solid sphere of radius 4 cm is
A)
64 done
clear
B)
16 done
clear
C)
12 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer69)
A cylindrical rod, whose height is 8 times its radius, is melted and cast into spherical balls of the same radius. The total number of spherical balls, so formed, is
A)
3 done
clear
B)
4 done
clear
C)
6 done
clear
D)
8 done
clear
View Solution play_arrow
-
question_answer70)
The areas of three adjacent faces of a cuboid are \[x\], y and z, then the volume of the cuboid is
A)
\[xy\] done
clear
B)
\[xyz\] done
clear
C)
\[\sqrt{xyz}\] done
clear
D)
\[\sqrt[3]{xyz}\] done
clear
View Solution play_arrow
-
question_answer71)
Three metal cubes of volume \[\text{125c}{{\text{m}}^{\text{3}}},\text{64c}{{\text{m}}^{\text{3}}}\]and \[\text{27c}{{\text{m}}^{\text{3}}}\]are melted to form a new cube, then the edge of the new cube formed is
A)
12 cm done
clear
B)
6 cm done
clear
C)
20 cm done
clear
D)
10 cm done
clear
View Solution play_arrow
-
question_answer72)
The perimeter of one face of a cube is 20 m, then its volume is
A)
\[\text{8}00\text{ }{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{1}000\text{ }{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{125 }{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{4}00\text{ }{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer73)
A closed box made of steel of uniform thickness has length, breadth and height 12 dm, 10 dm and 8 dm respectively. If the thickness of the steel sheet is 1 dm, then the inner surface area is
A)
\[\text{456 d}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{376 d}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{264 d}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{696 d}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer74)
The outer length, breadth and height of a box open at the top are 10 dm, 8 dm and 5 dm respectively. If the thickness of the wood is 1 dm, then the total surface area of the box is
A)
\[\text{42}0\text{ d}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{452 d}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{451 d}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{483 d}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer75)
A horse is placed for grazing inside a square field 12 cm long and is tethered to one corner by a rope 8 cm long. The area it can graze is
A)
50.18 sq cm done
clear
B)
50.28 sq cm done
clear
C)
50.38 sq cm done
clear
D)
50.48 sq cm done
clear
View Solution play_arrow
-
question_answer76)
Three squares have perimeters of 12 m, 20 m and 24 m respectively. If a rectangle is constructed whose area is equal to the combined area of the three squares such that its width is 7 m, then the length of the rectangle is
A)
6m done
clear
B)
8m done
clear
C)
10 m done
clear
D)
12m done
clear
View Solution play_arrow
-
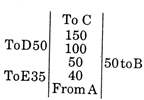
question_answer77)
A land surveyor records the various treatments of a field in his measurement book as given below. The area of the field surveyed is (all readings are in metres)
A)
6,000 sq m done
clear
B)
7,000 sq m done
clear
C)
7,500 sq m done
clear
D)
8,250 sq m done
clear
View Solution play_arrow
-
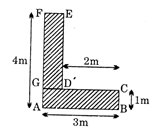
question_answer78)
Area of shaded portion as shown in the given figure is
A)
\[5\,{{m}^{2}}\] done
clear
B)
\[6\,{{m}^{2}}\] done
clear
C)
\[7\,{{m}^{2}}\] done
clear
D)
\[8\,{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer79)
If each edge of a cube is increased by 50%, then the percentage increase in the surface area is
A)
50 done
clear
B)
125 done
clear
C)
150 done
clear
D)
300 done
clear
View Solution play_arrow
-
question_answer80)
If T, V and 'K of a cuboid are increased, decreased and increased by 1%, 3% and 2% respectively, then the volume of the cuboid
A)
increases done
clear
B)
decreases done
clear
C)
increases or decreases depending on original dimensions done
clear
D)
Can't be calculated with given data done
clear
View Solution play_arrow
-
question_answer81)
The volume of a right circular cylinder, whose diameter is 10 cm and height 4 cm, is
A)
\[\text{4}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{2}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{1}00\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{8}0\text{ }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer82)
If the side of a regular hexagon is 6 cm, then its area will be
A)
90.43 sq cm done
clear
B)
93.53 sq cm done
clear
C)
93.63 sq cm done
clear
D)
93.73 sq cm done
clear
View Solution play_arrow
-
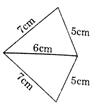
question_answer83)
The lengths of four sides and a diagonal of the given quadrilateral are indicated in the diagram If A denotes the area and \[l\] the length of the other diagonal, then A and \[l\] are respectively
A)
\[12\sqrt{6},4\sqrt{6}\] done
clear
B)
\[12\sqrt{6},5\sqrt{6}\] done
clear
C)
\[6\sqrt{6},4\sqrt{6}\] done
clear
D)
\[6\sqrt{6},5\sqrt{6}\] done
clear
View Solution play_arrow
-
question_answer84)
A unit cube is cut into two equal halves by a plane section parallel to one of its faces. The total surface area of both the halves is
A)
6 sq cm done
clear
B)
7 sq cm done
clear
C)
8 sq cm done
clear
D)
9 sq cm done
clear
View Solution play_arrow
-
question_answer85)
A box measures \[\text{3}0\text{cm}\times \text{24 cm}\times \text{18}\] cm. The longest rod that can be placed in it has the length
A)
16 cm done
clear
B)
30 cm done
clear
C)
42.42 cm done
clear
D)
42.52 cm done
clear
View Solution play_arrow
-
question_answer86)
A metal pipe has an external diameter of 4 cm and internal diameter of 3 cm and is 20 cm long, then the volume of the metal used is
A)
\[\text{22 c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{11}0\text{ c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{22}0\text{ c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{44}0\text{c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer87)
The radius of the base and the height of a right circular cylinder are each increased by 10%, then the volume of the cylinder is increased by
A)
30% done
clear
B)
40% done
clear
C)
42% done
clear
D)
33.1% done
clear
View Solution play_arrow
-
question_answer88)
A rectangular paper of dimensions 6 cm and 3 cm is rolled to form a cylinder with height equal to the width of the paper, then its base radius is
A)
\[\frac{6}{\pi }cm\] done
clear
B)
\[\frac{3}{2\pi }cm\] done
clear
C)
\[\frac{6}{2\pi }cm\] done
clear
D)
\[\frac{9}{2\pi }cm\] done
clear
View Solution play_arrow
-
question_answer89)
If the surface area of a cube is 384 sq m, then its volume is
A)
\[\text{51}0\text{ }{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{511 }{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{512 }{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{513 }{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer90)
The length of a hall with a flat roof is 20 m and width is 16 m. If the sum of the areas of the floor and roof is equal to the total area of the 4 walls, then the ratio of the Numerical value of the height to the volume of the hall is
A)
1 : 600 done
clear
B)
1: 200 done
clear
C)
1 : 240 done
clear
D)
1: 320 done
clear
View Solution play_arrow
-
question_answer91)
The curved surface area of a right circular cone with height 24 cm and radius 7 cm is
A)
\[\text{5}00\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{55}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{6}0\text{7 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{65}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer92)
It a regular square pyramid has a base of side 8 cm and height of 30 cm, then its volume is
A)
120 c.c. done
clear
B)
240 c.c. done
clear
C)
640 c.c. done
clear
D)
900 c.c. done
clear
View Solution play_arrow
-
question_answer93)
A cylinder circumscribes a sphere. The ratio of their volumes is
A)
1 : 2 done
clear
B)
2 : 3 done
clear
C)
3 : 4 done
clear
D)
5 : 6 done
clear
View Solution play_arrow
-
question_answer94)
From a right circular cylinder of radius\[\text{1}0\text{cm}\times \]height 21 cm a right circular cone of same base radius is removed. If the volume of the remaining portion is 4,400 cm3, then the height of the cone removed is
A)
15 cm done
clear
B)
18 cm done
clear
C)
21 cm done
clear
D)
24 cm done
clear
View Solution play_arrow
-
question_answer95)
If the radius and slant height of a right circular cone are 4 cm and 7 cm respectively, then its curved surface area will be
A)
\[\text{78 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{87 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{88 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{74 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer96)
A rectangular sheet of paper 22 cm long and 10 cm broad can be curved to form the lateral surface area of a right circular cylinder in two ways. Then the difference between the volumes of the two cylinders thus formed is
A)
\[\text{2}00\text{ c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{21}0\text{ c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{25}0\text{ c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{252 c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer97)
The volume of a right circular cone of height 8 cm and radius of base 3 cm is
A)
\[\text{12 }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{24 }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{48 }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{72 }\pi \text{ c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer98)
The height and base radius of a cone are each increased by 100%, then the volume of the cone becomes
A)
double done
clear
B)
three times done
clear
C)
six times done
clear
D)
eight times done
clear
View Solution play_arrow
-
question_answer99)
The radius and height of a cone are each increased by 20%, then the volume of the cone is increased by
A)
20% done
clear
B)
40% done
clear
C)
60% done
clear
D)
72.8% done
clear
View Solution play_arrow
-
question_answer100)
LOO. A conical container of base radius \['r'\] and height \['h'\]is full of water which is poured into a cylindrical container of radius r, then it will occupy a height equal to
A)
\[3{{m}^{2}}h\] done
clear
B)
\[\frac{h}{3{{m}^{2}}}\] done
clear
C)
\[\frac{mh}{3}\] done
clear
D)
\[\frac{3h}{m}\] done
clear
View Solution play_arrow
-
question_answer101)
The area of a rhombus is equal to
A)
product of its diagonals done
clear
B)
half of the product of its diagonals done
clear
C)
twice the product of its diagonals done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer102)
If a square and a rhombus stand on the same base, then the ratio of the areas of the square and the rhombus is equal to when one angle of rhombus is of \[30{}^\circ \]
A)
2 done
clear
B)
1 done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
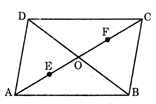
question_answer103)
If ABCD is a parallelogram and E, F the centroids of triangles ABD and BCD respectively, then EF equals
A)
AE done
clear
B)
BE done
clear
C)
CE done
clear
D)
DE done
clear
View Solution play_arrow
-
question_answer104)
The line segments AB and BC are perpendicular to each other. If AB = 4 cm and BC = 3 cm, then radius of the circle passing through A, B, C will be
A)
3.5 cm done
clear
B)
2.0 cm done
clear
C)
2.5 cm done
clear
D)
4.5 cm done
clear
View Solution play_arrow
-
question_answer105)
The diagonal of a cyclic square is a
A)
diameter done
clear
B)
radius done
clear
C)
tangent done
clear
D)
chord not necessarily the diameter of the circle done
clear
View Solution play_arrow
-
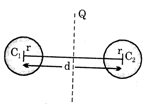
question_answer106)
Two circles of equal radii r, are at a distance d apart such that pairs of tangents are drawn to the circles from different points on the plane of the circles are equal, then all such points will lie on
A)
a circle done
clear
B)
a straight line equidistant from the circles done
clear
C)
a straight line bisecting the distance d done
clear
D)
none of the above done
clear
View Solution play_arrow
-
question_answer107)
The locus of the centres of the circles passing through two fixed points A and B is
A)
the circle whose diameter is AB done
clear
B)
the circle with a diameter perpendicular to AB done
clear
C)
the perpendicular bisector of the line AB done
clear
D)
none of the above done
clear
View Solution play_arrow
-
question_answer108)
If each side of an equilateral triangle be increased by 2 cm, its area is increased by\[2\sqrt{3}\]sq. cm. The length of each side of the original triangle is
A)
1cm done
clear
B)
\[\sqrt{3}\] done
clear
C)
3 cm done
clear
D)
\[\sqrt{3}+2\,cm\] done
clear
View Solution play_arrow
-
question_answer109)
A circular area having a radius 20 cm is divided into two equal parts by a concentric circle of radius 'r? The value of \['r'\] will be
A)
5 cm done
clear
B)
10 cm done
clear
C)
\[5\sqrt{2}\,cm\] done
clear
D)
\[10\sqrt{2}\,cm\] done
clear
View Solution play_arrow
-
question_answer110)
If the length of each side of an equilateral triangle is equal to the radius of a circle of area 154 sq. cm., then the area of the equilateral triangle is
A)
\[\frac{7\sqrt{3}}{4}sq.\,cm\] done
clear
B)
\[\frac{49\sqrt{3}}{4}sq.\,cm\] done
clear
C)
35 sq. cm done
clear
D)
49 sq. cm done
clear
View Solution play_arrow
-
question_answer111)
A plot of ground is in the form of an isosceles triangle. The cost of the triangular land is Rs. 50,000 at the rate of Rs. 125per square metre If the length of the base is 40m, then the length of equal sides is
A)
\[20\sqrt{3}\,m\]m done
clear
B)
\[22\sqrt{3}\,m\] done
clear
C)
\[22\sqrt{2}\,m\] done
clear
D)
\[20\sqrt{2}\,m\] done
clear
View Solution play_arrow
-
question_answer112)
The whole surface of a cubic is \[\text{216 c}{{\text{m}}^{\text{2}}}\]The volume of this will be
A)
\[\text{1}0\text{8 c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\text{54 c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\text{432 c}{{\text{m}}^{\text{3}}}\] done
clear
D)
\[\text{216 c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer113)
The corner of a cube has been cut by the plan passing through mid-point of the three edge meeting at that corner. If the edge of the cube is of 2 cm length, then the volume of the pyramid thus cut off is
A)
\[\frac{1}{24}\]\[\text{c}{{\text{m}}^{\text{3}}}\] done
clear
B)
\[\frac{1}{6}\]\[\text{c}{{\text{m}}^{\text{3}}}\] done
clear
C)
\[\frac{1}{48}\]\[\text{c}{{\text{m}}^{\text{3}}}\] done
clear
D)
6 \[\text{c}{{\text{m}}^{\text{3}}}\] done
clear
View Solution play_arrow
-
question_answer114)
There is a cylinder circumscribing the hemisphere such that their bases are common. The ratio of their volume is
A)
1: 3 done
clear
B)
1 : 2 done
clear
C)
2 : 3 done
clear
D)
3 : 4 done
clear
View Solution play_arrow
-
question_answer115)
A square and an equilateral triangle have the same perimeter. If the diagonal of the square is \[12\sqrt{2}\] cm? then the area of the triangle is
A)
\[64\sqrt{3}\,c{{m}^{2}}\] done
clear
B)
\[32\sqrt{3}\,c{{m}^{2}}\] done
clear
C)
\[24\sqrt{3}\,c{{m}^{2}}\] done
clear
D)
\[24\sqrt{2}\,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer116)
A horse is tied to a vertex of a field having the shape of an equilateral triangle with a rope, the length of which is half of the length of a side of the triangle. The percentage of the total area of the field over which the horse can graze is approximately
A)
20 to 22% done
clear
B)
25 to 27% done
clear
C)
30 to 32% done
clear
D)
48 to 50% done
clear
View Solution play_arrow
-
question_answer117)
In a right-angled triangle, the lengths of the sides containing the right angle are a and b. With the midpoint of each side as centre, three semicircular areas are drawn outside the triangle. The total area enclosed is
A)
\[\frac{\pi }{2}({{a}^{2}}+{{b}^{2}})+\frac{1}{8}{{(a+b)}^{2}}\] done
clear
B)
\[\frac{\pi }{2}({{a}^{2}}+{{b}^{2}})+\frac{1}{2}ab\] done
clear
C)
\[\frac{\pi }{2}({{a}^{2}}+{{b}^{2}})+\frac{1}{8}{{(a+b)}^{2}}\] done
clear
D)
\[\frac{\pi }{4}({{a}^{2}}+{{b}^{2}})+\frac{1}{2}ab\] done
clear
View Solution play_arrow
-
question_answer118)
P and Q are the midpoints of the side AB and AC , respectively of a triangle ABC. The ratio of the y area of the trapezium PQCB to the area of the triangle APQ is
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer119)
If the number of units in the circumference of a circle is same as the number of units in the area, then the radius of the circle will be
A)
1 unit done
clear
B)
2 units done
clear
C)
3 units done
clear
D)
4 units done
clear
View Solution play_arrow
-
question_answer120)
The side of a square is 2 cm. Semicircles are constructed on two sides of the square, then the area of the whole figure is
A)
\[\left( \text{4}+\pi \right)\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\left( \text{4 }+\text{ 4}\pi \right)\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{4}\pi \text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{8}\pi \text{ c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer121)
A piece of wire 132 dm long is bent successively in the shape of an equilateral triangle, a square, a regular hexagon and a circle. Then the area included is largest when the shape is
A)
triangle done
clear
B)
square done
clear
C)
hexagon done
clear
D)
circle done
clear
View Solution play_arrow
-
question_answer122)
A wire, in the shape of an equilateral triangle, encloses an area 'S'\[\text{c}{{\text{m}}^{\text{2}}}\]. If the same wire is bent to form a circle, then the area of the circle will be
A)
\[\frac{\pi {{S}^{2}}}{\pi }\] done
clear
B)
\[\frac{3{{S}^{2}}}{\pi }\] done
clear
C)
\[\frac{3S}{\pi }\] done
clear
D)
\[\frac{3S\sqrt{3}}{\pi }\] done
clear
View Solution play_arrow
-
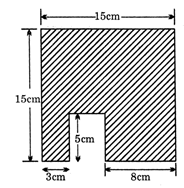
question_answer123)
The radius of the base of a right circular cone is r and its height is 2h, then its volume is
A)
\[\frac{2}{3}\pi {{r}^{2}}h\] done
clear
B)
\[\pi {{r}^{2}}h\] done
clear
C)
\[2\pi {{r}^{3}}h\] done
clear
D)
\[8\,\pi \,c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer124)
If the curved surface of a cylinder be doubled the area of the ends, then the ratio of its height and radius is
A)
2 : 3 done
clear
B)
1 : 1 done
clear
C)
2 : 1 done
clear
D)
1 : 2 done
clear
View Solution play_arrow
-
question_answer125)
If the numerical value of the surface area of a cube is equal to the numerical value of the volume of the cube, then the numerical value of area of each face of the cube is
A)
1 done
clear
B)
6 done
clear
C)
12 done
clear
D)
36 done
clear
View Solution play_arrow
-
question_answer126)
A cuboid has a volume of 64000 cm3. If the ratio of its sides are 1:2:4, then the largest side is
A)
40 cm done
clear
B)
60 cm done
clear
C)
64 cm done
clear
D)
80 cm done
clear
View Solution play_arrow
-
question_answer127)
If three cubes of metal whose edges are 30 cm, 40 cm and 50 cm respectively are melted and formed into a single cube, the total surface area of the single new cube is
A)
\[\text{2}.0{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{2}.\text{15}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{2}.\text{16}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{2}.\text{2}{{\text{m}}^{2}}\] done
clear
View Solution play_arrow
-
question_answer128)
A wall 4 metre long, 3 metre high and 13 cm thick is made up of bricks each measuring\[\text{2}0\text{cm}\times \text{12cm}\times \text{6}.\text{5cm}\]. The number of bricks required is
A)
500 done
clear
B)
1000 done
clear
C)
1500 done
clear
D)
2000 done
clear
View Solution play_arrow
-
question_answer129)
The section of a right circular cone by a plane through its vertex perpendicular to the base is an equilateral triangle of side 12 cm. The volume of the cone is
A)
\[72\sqrt{3}\,\pi \,c{{m}^{3}}\] done
clear
B)
\[71\sqrt{3}\,\pi \,c{{m}^{3}}\] done
clear
C)
\[70\sqrt{2}\,\pi \,c{{m}^{3}}\] done
clear
D)
\[69\sqrt{2}\,\pi \,c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer130)
Two cubes have volumes in the ratio 1 : 27, then the ratio of the area of the face of one to that of the other is
A)
1 : 3 done
clear
B)
1 : 6 done
clear
C)
1 : 9 done
clear
D)
1: 18 done
clear
View Solution play_arrow
-
question_answer131)
The ratio of the height of a circular cylinder to the diameter of its base is 1 : 2, then the ratio of the areas of its curved surface to the sum of the areas of its two ends is
A)
1 : 1 done
clear
B)
1 : 2 done
clear
C)
2 : 1 done
clear
D)
1 : 3 done
clear
View Solution play_arrow
-
question_answer132)
The curved surface of a circular cylinder of height\['h'\]and the curved surface area of the cone of slant height 2\['h'\]having the same circular base, are in the ratio of
A)
1 : 2 done
clear
B)
2 : 1 done
clear
C)
1 : 1 done
clear
D)
1 : 3 done
clear
View Solution play_arrow
-
question_answer133)
The volume of the greatest sphere cut off from a cylindrical wood of base radius 1 cm and height 5 cm is
A)
\[\frac{4}{3}\times (5\pi )\,c{{m}^{3}}\] done
clear
B)
\[\frac{4}{3}\times \pi \,c{{m}^{3}}\] done
clear
C)
\[5\pi \,c{{m}^{3}}\] done
clear
D)
\[\frac{10\pi }{3}\,c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer134)
Consider two cones, the curved surface area of one being twice that of the other and the slant height of the latter being twice that of the former. The ratio of the radius of the latter cone to that of the former is
A)
1 : 4 done
clear
B)
1 : 2 done
clear
C)
2 : 1 done
clear
D)
4 : 1 done
clear
View Solution play_arrow
-
question_answer135)
A right pyramid stands on a rectangular base whose sides are 24 cm and 18 cm and each of the slant edges is 17 cm. The height of he pyramid is
A)
8 cm done
clear
B)
10cm done
clear
C)
12cm done
clear
D)
15cm done
clear
View Solution play_arrow
-
question_answer136)
A pyramid is formed by cutting off a corner of a cube whose edge is two metres by a plane which bisects its three co-terminus edges. The volume of the pyramid is
A)
\[1\,{{m}^{3}}\] done
clear
B)
\[\frac{1}{2}\,{{m}^{3}}\] done
clear
C)
\[\frac{1}{3}\,{{m}^{3}}\] done
clear
D)
\[\frac{1}{6}\,{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer137)
A solid cylinder of glass whose diameter is 1.5 m and height 1 m is melted and recasted into a sphere, then the radius of the sphere is
A)
1m done
clear
B)
0.75 m done
clear
C)
1.25 m done
clear
D)
1.5 m done
clear
View Solution play_arrow
-
question_answer138)
The area of the shaded region is
A)
\[\text{15}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{14}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{2}0\text{5 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{12}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer139)
Consider a hollow cylinder of inner radius r and thickness of wall t and length\[l\]. The volume of the above cylinder is given by
A)
\[2\pi l({{r}^{2}}-{{l}^{2}})\] done
clear
B)
\[2\pi rl\left( \frac{1}{2r}+1 \right)\] done
clear
C)
\[2\pi l({{r}^{2}}+{{t}^{2}})\] done
clear
D)
\[2\pi l(r+{{t}^{2}})\] done
clear
View Solution play_arrow
-
question_answer140)
A sphere has the same curved surface as the total surface area of cylinder of height 4 cm diameter of base 8 cm. The radius of the sphere is
A)
2 cm done
clear
B)
3cm done
clear
C)
4 cm done
clear
D)
6 cm done
clear
View Solution play_arrow
-
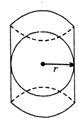
question_answer141)
A sphere of radius \['r'\] is inscribed in the cylind such that the curved surface of the sphere touch the cylinder as shown in the given figure. The area of curved surface of cylinder is
A)
\[\frac{4}{3}\pi {{r}^{2}}\] done
clear
B)
\[4\pi {{r}^{2}}\] done
clear
C)
\[\pi {{r}^{2}}\] done
clear
D)
\[2\,\pi {{r}^{2}}\] done
clear
View Solution play_arrow
-
question_answer142)
Two circular cylinders of equal volume have their heights in the ratio 1:3. The ratio of their radii is
A)
\[4:\sqrt{3}\] done
clear
B)
\[3:2\sqrt{3}\] done
clear
C)
\[2:\sqrt{3}\] done
clear
D)
\[3:\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer143)
The area of a rectangular field is 150 sq. units. If its perimeter is 50 units, then its dimensions are
A)
27, 5 done
clear
B)
3, 50 done
clear
C)
5, 30 done
clear
D)
10, 15 done
clear
View Solution play_arrow
-
question_answer144)
The diagonal of a rectangle is thrice its smaller side. The ratio of the sides is
A)
\[2\sqrt{2}:1\] done
clear
B)
3 : 2 done
clear
C)
\[\sqrt{3}:1\] done
clear
D)
\[\sqrt{2}:1\] done
clear
View Solution play_arrow
-
question_answer145)
If each side of a rectangle is increased by 50%, then its area will be increased by
A)
150% done
clear
B)
120% done
clear
C)
125% done
clear
D)
None of these done
clear
View Solution play_arrow
-
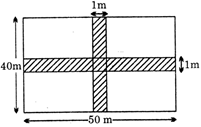
question_answer146)
The area of the shaded region in the adjoining figure is
A)
\[\text{2}000\text{ }{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{9}0\text{ }{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{45}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{89}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer147)
The outer length, breadth and height of a wooden 5 box open at the top are 10 cm, 8 cm and 5 cm % respectively. If the thickness of the wood is 1 cm, the total surface area of the box is
A)
420 sq. cm done
clear
B)
452 sq. cm done
clear
C)
451 sq. cm done
clear
D)
483 sq. cm done
clear
View Solution play_arrow
-
question_answer148)
A closed vessel the inside of which is a circular cone of height h contains some water in it. When the cone is vertical with its vertex downwards, the water stands to a height \[\frac{h}{2}\]. To what height will it stand when the vessel is inverted?
A)
\[\frac{h}{2}\] done
clear
B)
\[\frac{{{h}^{\frac{1}{3}}}}{2}\] done
clear
C)
\[{{7}^{\frac{1}{3}}}\frac{h}{2}\] done
clear
D)
\[h\left( 1-\frac{{{7}^{\frac{1}{3}}}}{2} \right)\] done
clear
View Solution play_arrow
-
question_answer149)
If the radius of the base of a cylinder is 2 cm and its height 7 cm, then its curved surface is
A)
\[\text{44 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{22 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{88c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{56c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer150)
If the sides of an equilateral triangle are given by \[\text{2a}-\text{6}-\text{3},\text{a}-\text{b}+\text{1}\] and\[\text{2a}-\text{2b}-\text{1}\], then the perimeter (in cms) of the triangle is
A)
6 done
clear
B)
9 done
clear
C)
12 done
clear
D)
15 done
clear
View Solution play_arrow
-
question_answer151)
If the perimeter of an equilateral triangle is equal to the circumference of a circle, then the ratio of their areas is
A)
\[\pi :\sqrt{3}\] done
clear
B)
\[\pi :3\] done
clear
C)
\[\pi :9\] done
clear
D)
\[\pi :3\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer152)
The length of a rectangle is 1 cm more than its breadth. A square of side \['p'\] has been cut out of it. If \['p'\] is one third the breadth of the rectangle, the remaining area is
A)
\[\left( \text{8}{{\text{p}}^{\text{2}}}+\text{3p} \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\left( \text{3}{{\text{p}}^{\text{2}}}+\text{8p} \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\left( \text{8}{{\text{p}}^{\text{2}}}+\text{8} \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\left( \text{3}{{\text{p}}^{\text{2}}}+\text{8} \right)\text{c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer153)
The length of a rectangle exceeds its breadth by 5 cm. Two vertices of a triangle coincide with that of the rectangle and the third vertex lies on the opposite side of the rectangle. The area of the remaining part is
A)
half that of the rectangle done
clear
B)
one-third that of the rectangle done
clear
C)
one fourth that of the rectangle done
clear
D)
none of these done
clear
View Solution play_arrow
-
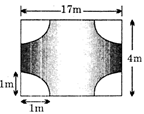
question_answer154)
The perimeter of the following shaded portion of the figure is
A)
40 m done
clear
B)
40.07 m done
clear
C)
40.28m done
clear
D)
35m done
clear
View Solution play_arrow
-
question_answer155)
If two parallel chords on the same side of the centre of a circle are 6 cm and 8 cm and they are 1 cm apart, then the diameter of the circle (in cm) is
A)
14 done
clear
B)
10 done
clear
C)
8 done
clear
D)
5 done
clear
View Solution play_arrow
-
question_answer156)
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is\[12\sqrt{2}\]cm, then the area (in\[\text{c}{{\text{m}}^{\text{2}}}\]) of the triangle is
A)
\[36\sqrt{2}\] done
clear
B)
\[36\sqrt{3}\] done
clear
C)
\[64\sqrt{2}\] done
clear
D)
\[64\sqrt{3}\] done
clear
View Solution play_arrow
-
question_answer157)
The perimeter of a right angled triangle is 60 cm and its hypotenuse is 26 cm, then the area of the triangle is
A)
\[\text{12}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{121c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{119 c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{125 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer158)
The side of a regular hexagon is y cm, then its area is
A)
\[\frac{\sqrt{3}}{2}{{p}^{2\,}}c{{m}^{2}}\] done
clear
B)
\[\frac{3\sqrt{3}}{2}{{p}^{2\,}}c{{m}^{2}}\] done
clear
C)
\[2\sqrt{3}\,{{p}^{2\,}}c{{m}^{2}}\] done
clear
D)
\[6\,{{p}^{2\,}}c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer159)
If a circle and a square have the same perimeter, then the
A)
circle and the square have equal area done
clear
B)
circle have larger area than the square done
clear
C)
square has larger area than the circle done
clear
D)
area of the square is double that of the circle done
clear
View Solution play_arrow
-
question_answer160)
A lawn 120 m by 80 m is surrounded by a path of 3 m width. The area (in\[{{\text{m}}^{\text{2}}}\]) of the path is
A)
1164 done
clear
B)
1236 done
clear
C)
8364 done
clear
D)
10836 done
clear
View Solution play_arrow
-
question_answer161)
The sides of a rectangular solid are 72 cm, 75 cm and 135 cm. The side of the cube (in cm) whose volume is equal to the solid, is
A)
75 done
clear
B)
80 done
clear
C)
85 done
clear
D)
90 done
clear
View Solution play_arrow
-
question_answer162)
A wire is in the form of a circle of radius 28 cm, then the side of the square into which it can be bent is
A)
\[\frac{\pi }{2}\]cm done
clear
B)
\[2\pi \]cm done
clear
C)
44 cm done
clear
D)
\[\left( \pi +\text{28} \right)\text{ cm}\] done
clear
View Solution play_arrow
-
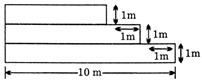
question_answer163)
The area of the given figure is
A)
\[\text{28 }{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{27 }{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{29 }{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{3}0\text{ }{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
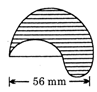
question_answer164)
The boundary of the shaded region in the adjoining figure is
A)
200 mm done
clear
B)
196 mm done
clear
C)
186 mm done
clear
D)
176 mm done
clear
View Solution play_arrow
-
question_answer165)
The volume of a sphere is \[\frac{4}{3}\pi {{r}^{3}}\] c.c. What is the ratio of the volume of a cube to that of a sphere which will fit inside the cube?
A)
\[\text{4 }:\text{ 3}\pi \] done
clear
B)
\[2:\text{ }\pi \] done
clear
C)
\[8:\text{ }\pi \] done
clear
D)
\[6:\text{ }\pi \] done
clear
View Solution play_arrow
-
question_answer166)
Each edge of a cube is increased by 50%. The per cent of increase in the surface area of the cube is
A)
50 done
clear
B)
125 done
clear
C)
750 done
clear
D)
300 done
clear
View Solution play_arrow
-
question_answer167)
The sides of a triangle are 3 cm, 4 cm and 5 cm. Its area is
A)
\[\text{12 c}{{\text{m}}^{\text{2}}}\] done
clear
B)
\[\text{15 c}{{\text{m}}^{\text{2}}}\] done
clear
C)
\[\text{2}0\text{ c}{{\text{m}}^{\text{2}}}\] done
clear
D)
\[\text{6 c}{{\text{m}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer168)
A rectangular sheet of metal, \[x\] cm by y cm ha square of side z cm cut from each corner The sheet is then bent to form a tray of depth z cm. The volume of the tray is
A)
\[z(x-z)(y-z)c.c\]. done
clear
B)
\[xyz\,c.c.\] done
clear
C)
\[z(x-2z)(y-2z)c.c\] done
clear
D)
\[(x+y)z\,c.c\] done
clear
View Solution play_arrow
-
question_answer169)
A rectangular container A which is 100 cm by 75 cm by 25 cm, is full of water. Some of this water is used to fill completely another container B measuring 50 cm by 50 by 25 cm. The volume of water (in litres) left over in A, is
A)
25 done
clear
B)
50 done
clear
C)
125 done
clear
D)
150 done
clear
View Solution play_arrow
-
question_answer170)
From four corners of a rectangular iron sheet of\[\text{24 cm}\times \text{3}0\text{ cm}\], four squares of side 6 cm are cut. The remaining portion of the sheet is formed into an open box. The internal volume (in\[\text{c}{{\text{m}}^{\text{3}}}\]) of the box is
A)
4300 done
clear
B)
2592 done
clear
C)
2542 done
clear
D)
1296 done
clear
View Solution play_arrow
-
question_answer171)
If the diagonal of cube is\[\sqrt{300}\]cms, then the surface area (in sq. cm) is
A)
300 done
clear
B)
600 done
clear
C)
1200 done
clear
D)
2400 done
clear
View Solution play_arrow
-
question_answer172)
If a rectangle of sides 5 cm and 15 cm is to be divided into three squares of equal area, then the sides of the squares will be
A)
4 cm done
clear
B)
6cm done
clear
C)
7 cm done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer173)
The area of the shaded region in the given figure, if every circle is of unit radius is
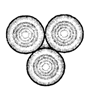
A)
\[\left( \sqrt{3}-\frac{\pi }{2} \right)sq.\,units\] done
clear
B)
\[(\sqrt{3}+\pi )sq.\,units\] done
clear
C)
\[\left( 2\sqrt{3}-\frac{\pi }{2} \right)sq.\,units\] done
clear
D)
\[\left( \sqrt{3}-\frac{\pi }{4} \right)sq.\,units\] done
clear
View Solution play_arrow
-
question_answer174)
The perimeter of a rhombus is 160 cm and one diagonal is 10 cm long, then length of the other diagonal is
A)
\[\sqrt{10}\]cm done
clear
B)
\[\sqrt{37}\]cm done
clear
C)
\[30\sqrt{7}\]cm done
clear
D)
\[\sqrt{\text{24}00}\] done
clear
View Solution play_arrow
-
question_answer175)
If six cubes of 10 cm edge are joined end to end, then the surface area (in sq. cm) of the resulting solid is
A)
3600 done
clear
B)
3000 done
clear
C)
2600 done
clear
D)
2400 done
clear
View Solution play_arrow
-
question_answer176)
If the volumes of a cone and a hemisphere having the same base are equal, then the height of the cone will be \[x\] times the radius of the base of hemisphere, where\[x\]x is
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
\[\pi \] done
clear
View Solution play_arrow
-
question_answer177)
A cone and a cylinder have the same base area. They also have the same curved surface area. If the height of the cylinder is 3m, then the slant height of the cone (in m) is
A)
3 done
clear
B)
4 done
clear
C)
6 done
clear
D)
7 done
clear
View Solution play_arrow
-
question_answer178)
If the volume of a prism is \[1920\sqrt{3}\,c{{m}^{3}}\]and the side of the equilateral base is 16 cm, then the height (in cm) of the prism is
A)
19 done
clear
B)
20 done
clear
C)
30 done
clear
D)
40 done
clear
View Solution play_arrow
-
question_answer179)
The base of the right pyramid is a square of side 16 cm and height 15 cm. Its volume (in\[\text{c}{{\text{m}}^{\text{3}}}\]) will be
A)
3840 done
clear
B)
1920 done
clear
C)
1280 done
clear
D)
960 done
clear
View Solution play_arrow
-
question_answer180)
An iron pipe is 0.35 m long, its external and internal diameter are 8 cm and 6 cm respectively. The volume (in cc) of the pipe is (given\[\pi =\frac{22}{7}\])
A)
7700 done
clear
B)
11000 done
clear
C)
770 done
clear
D)
77 done
clear
View Solution play_arrow
-
question_answer181)
The ratio of the volumes of two spheres is 8:27 The ratio of their radii is
A)
3 : 2 done
clear
B)
2 : 3 done
clear
C)
4 : 3 done
clear
D)
2 : 9 done
clear
View Solution play_arrow
-
question_answer182)
A sphere of radius 3 cms is dropped into a cylindrical vessel of radius 4 cms. If the sphere is submerged completely, then the height (in cm) to which the water rises, is
A)
2.35 done
clear
B)
2.30 done
clear
C)
2.25 done
clear
D)
2.15 done
clear
View Solution play_arrow
-
question_answer183)
A solid sphere of radius r cm is bisected along two perpendicular planes. The total surface area (in \[\text{c}{{\text{m}}^{\text{2}}}\] ) of the 4 pieces formed, is
A)
\[\text{4 }\pi \text{ }{{\text{r}}^{\text{2}}}\] done
clear
B)
\[\text{6 }\pi \text{ }{{\text{r}}^{\text{2}}}\] done
clear
C)
\[\text{8}\pi {{\text{r}}^{\text{2}}}\] done
clear
D)
\[\text{12 }\pi \text{ }{{\text{r}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer184)
A parallelogram whose sides are 10 cm and 5 cm has one diagonal of 8 cm, then the length of the other diagonal is
A)
12cm done
clear
B)
11 cm done
clear
C)
14 cm done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer185)
The area of the shaded region in the given figure is
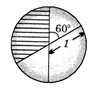
A)
\[\frac{\pi }{3}\] sq. units done
clear
B)
\[\frac{\pi }{2}\] sq. units done
clear
C)
\[\frac{\pi }{4}\] sq. units done
clear
D)
\[{{\pi }^{2}}\] sq. units done
clear
View Solution play_arrow
-
question_answer186)
The area of the shaded portion in the given figure is
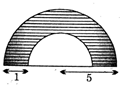
A)
7.5 \[\pi \] sq. units done
clear
B)
6.5 \[\pi \] sq. units done
clear
C)
5.5 \[\pi \] sq. units done
clear
D)
4.5 \[\pi \] sq. units done
clear
View Solution play_arrow
-
question_answer187)
A cuboid has
A)
4 edges done
clear
B)
8 edges done
clear
C)
12 edges done
clear
D)
16 edges done
clear
View Solution play_arrow
-
question_answer188)
In the adjoining figure, the radius of the inner circles, if other circles are of radii m units is
A)
B)
\[\sqrt{2}m\] done
clear
C)
\[\frac{1}{\sqrt{2}}m\] done
clear
D)
\[\frac{2}{\sqrt{2}+1}m\] done
clear
View Solution play_arrow
-
question_answer189)
A wire of length 50 cm is to be bent in the form of a parallelogram of area \[\text{5}0\text{ c}{{\text{m}}^{\text{2}}}\] . If the angle between the adjacent sides is \[30{}^\circ \], then the dimensions of the parallelogram are
A)
15 cm, 10 cm done
clear
B)
13 cm, 12 cm done
clear
C)
20 cm, 5 cm done
clear
D)
17 cm, 8 cm done
clear
View Solution play_arrow
-
question_answer190)
If every side of a triangle is doubled, then the area of the new triangle is 'K' times the area of the old one. The value of K is
A)
2 done
clear
B)
3 done
clear
C)
\[\sqrt{2}\] done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer191)
If the longer side of a rectangle is doubled and the other reduced to half, then the area of the new rectangle goes up by
A)
50% done
clear
B)
100% done
clear
C)
150% done
clear
D)
no change done
clear
View Solution play_arrow
-
question_answer192)
In a right triangle with sides a and 6, hypotenuse H, the altitude drawn on hypotenuse is p, then
A)
\[\text{a}+\text{b}=\text{H}+\text{p}\] done
clear
B)
\[\text{ab}=\text{HL}.\text{p}\] done
clear
C)
\[\text{ap}=\text{bH}\] done
clear
D)
\[{{\text{a}}^{\text{2}}}+{{\text{b}}^{\text{2}}}={{\text{H}}^{\text{2}}}+{{\text{p}}^{\text{2}}}\] done
clear
View Solution play_arrow
-
question_answer193)
It \[l\] , b, h are the length, breadth and height of a room, then area of 4 walls will be
A)
\[\text{2}\left( l\text{ }+\text{ b} \right)\text{h}\] done
clear
B)
\[\left( l\text{ }+\text{ b} \right)\text{h}\] done
clear
C)
\[lbh\] done
clear
D)
\[\text{2}\left( l\text{b}+\text{bh}+\text{h}l \right)\] done
clear
View Solution play_arrow











 \[(\sqrt{2}-1)m\] done
clear
\[(\sqrt{2}-1)m\] done
clear
