Category : JEE Main & Advanced
Projection of a line joining the points\[\mathbf{P(}{{\mathbf{x}}_{\mathbf{1}}}\mathbf{,}{{\mathbf{y}}_{\mathbf{1}}}\mathbf{,}{{\mathbf{z}}_{\mathbf{1}}}\mathbf{)}\] and \[\mathbf{Q(}{{\mathbf{x}}_{\mathbf{2}}}\mathbf{,}{{\mathbf{y}}_{\mathbf{2}}}\mathbf{,}{{\mathbf{z}}_{\mathbf{2}}}\mathbf{)}\] on another line whose direction cosines are \[\mathbf{l,}\,\,\mathbf{m}\] and \[\mathbf{n}\] : Let PQ be a line segment where \[P\equiv ({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}})\] and \[Q\equiv ({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}})\] and AB be a given line with d.c.’s as \[l,\,\,m,\,\,n\]. If the line segment PQ makes angle \[\theta \] with the line AB, then
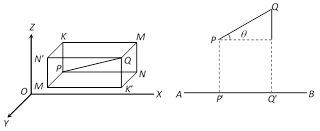
Projection of PQ is \[P'Q'=PQ\cos \,\theta \]
\[=({{x}_{2}}-{{x}_{1}})\cos \alpha +({{y}_{2}}-{{y}_{1}})\cos \beta +({{z}_{2}}-{{z}_{1}})\cos \gamma \]
\[=({{x}_{2}}-{{x}_{1}})l+({{y}_{2}}-{{y}_{1}})m+({{z}_{2}}-{{z}_{1}})n\].
For x-axis,\[l=1,\,\,m=0,\,\,n=0\].
Hence, projection of PQ on x-axis \[={{x}_{2}}-{{x}_{1}}\].
Similarly, projection of PQ on y-axis \[={{y}_{2}}-{{y}_{1}}\] and projection of PQ on z-axis \[={{z}_{2}}{{z}_{1}}\].
You need to login to perform this action.
You will be redirected in
3 sec
