Category : JEE Main & Advanced
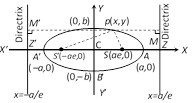
Let S be the focus, ZM be the directrix of the ellipse and \[P(x,y)\]is any point on the ellipse, then by definition \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\], where \[{{b}^{2}}={{a}^{2}}(1-{{e}^{2}})\].
Since \[e<1\], therefore \[{{a}^{2}}(1-{{e}^{2}})<{{a}^{2}}\] Þ \[{{b}^{2}}<{{a}^{2}}\].
The other form of equation of ellipse is \[\frac{{{x}^{2}}}{{{y}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\], where, \[{{a}^{2}}={{b}^{2}}(1-{{e}^{2}})\,i.e.,\,a<b\].
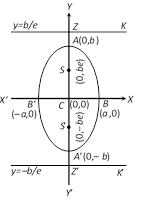
Difference between both ellipses will be clear from the following table :
| Ellipse | \[\left\{ \frac{{{x}^{\mathbf{2}}}}{{{a}^{\mathbf{2}}}}+\frac{{{y}^{\mathbf{2}}}}{{{b}^{\mathbf{2}}}}=\mathbf{1} \right\}\] | |
| Imp. terms | ||
| For \[\mathbf{a>b}\] | For \[\mathbf{b>a}\] | |
| Centre | \[(0,\,\,0)\] | \[(0,\,\,0)\] |
| Vertices | \[(\pm a,\,0)\] | \[(0,\,\pm b)\] |
| Length of major axis | \[2a\] | \[2b\] |
| Length of minor axis | \[2b\] | \[2a\] |
| Foci | \[(\pm ae,\,0)\] | \[(0,\pm \,be)\] |
| Equation of directrices | \[x=\pm a/e\] | \[y=\pm b/e\] |
| Relation in a, b and e | \[{{b}^{2}}={{a}^{2}}(1-{{e}^{2}})\] | \[{{a}^{2}}={{b}^{2}}(1-{{e}^{2}})\] |
| Length of latus rectum | \[\frac{2{{b}^{2}}}{a}\] | \[\frac{2{{a}^{2}}}{b}\] |
| Ends of latus-rectum | \[\left( \pm ae,\pm \frac{{{b}^{2}}}{a} \right)\] | \[\left( \pm \frac{{{a}^{2}}}{b},\pm be \right)\] |
| Parametric equations | \[(a\cos \phi ,b\sin \phi )\] | \[(a\cos \varphi ,b\sin \varphi )\] \[(0\le \phi <2\pi )\] |
| Focal radii | \[SP=a-e{{x}_{1}}\] \[S'P=a+e{{x}_{1}}\] | \[SP=b-e{{y}_{1}}\] \[S'P=b+e{{y}_{1}}\] |
| Sum of focal radii \[SP+S'P=\] | \[2a\] | \[2b\] |
| Distance between foci | \[2ae\] | \[2be\] |
| Distance between directrices | \[2a/e\] | \[2b/e\] |
| Tangents at the vertices | \[x=a,\text{ }x=a\] | \[y=b,y=b\] |
You need to login to perform this action.
You will be redirected in
3 sec
