Category : JEE Main & Advanced
(1) Shifting of origin without rotation of axes : Let \[P\equiv (x,y)\]with respect to axes \[OX\] and \[OY\].
Let \[O'\equiv (\alpha ,\beta )\] with respect to axes \[OX\] and \[OY\] and let \[P\equiv (x',y')\] with respect to axes \[O'X'\] and \[O'Y',\] where \[OX\] and \[O'X'\] are parallel and \[OY\] and \[O'Y'\] are parallel.

Then \[x=x'+\alpha ,\text{ }y=y'\,+\beta \]
or \[x'=x-\alpha ,\text{ }y'=y-\beta \]
Thus if origin is shifted to point \[(\alpha ,\beta )\] without rotation of axes, then new equation of curve can be obtained by putting \[x+\alpha \] in place of \[x\] and \[y+\beta \] in place of \[y\].
(2) Rotation of axes without changing the origin : Let \[O\] be the origin. Let \[P\equiv (x,y)\] with respect to axes \[OX\] and \[OY\] and let \[P\equiv (x',y')\] with respect to axes \[OX'\] and \[OY'\] where \[\angle X'OX=\angle YOY'=\theta \]
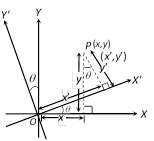
then \[x=x'\cos \theta -y'\sin \theta \]
\[y=x'\sin \theta +y'\cos \theta \]
and \[x'=x\cos \theta +y\sin \theta \]
\[y'=-x\sin \theta +y\cos \theta \]\[\]
The above relation between \[(x,y)\] and \[(x',y')\] can be easily obtained with the help of following table
| \[x\downarrow \] | \[y\downarrow \] | |
| \[x'\to \] \[y'\to \] | \[\cos \theta \] \[-\sin \theta \] | \[\sin \theta \] \[\cos \theta \] |
(3) Change of origin and rotation of axes : If origin is changed to \[O'(\alpha ,\beta )\] and axes are rotated about the new origin \[O'\] by an angle \[\theta \] in the anti-clockwise sense such that the new co-ordinates of \[P(x,y)\] become \[(x',y')\] then the equations of transformation will be \[x=\alpha +x'\cos \theta -y'\sin \theta \] and \[y=\beta +x'\sin \theta +y'\cos \theta \]
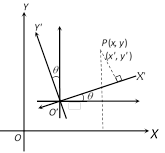
(4) Reflection (Image of a point) : Let \[(x,y)\]be any point, then its image with respect to
(i) x-axis \[\Rightarrow \] \[(x,-y)\]
(ii) y-axis \[\Rightarrow \] \[(-x,y)\]
(iii) origin \[\Rightarrow \] \[(-x,-y)\]
(iv) line \[y=x\]\[\Rightarrow \]\[(y,x)\]
You need to login to perform this action.
You will be redirected in
3 sec
