9th Class Mathematics Triangles Question Bank

done Triangle Total Questions - 30

• question_answer1)
  If one angle of a triangle is equal to half of the sum of the other two equal angles, then the triangle is:
  A)
   Isosceles                       done clear
  B)
   Scalene done clear
  C)
   Equilateral        done clear
  D)
   Right angled done clear
  View Solution play_arrow

• question_answer2)
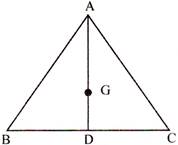
  In the figure given below, G is the centroid of the equilateral triangle ABC, If \[\mathbf{AB}=\mathbf{6}\] cm, then AG is equal to
  A)
   \[\sqrt{3}\]cm                            done clear
  B)
   \[3\sqrt{2}\]cm. done clear
  C)
   \[\frac{3\sqrt{3}}{2}\] cm                   done clear
  D)
   \[2\sqrt{3}\]cm. done clear
  View Solution play_arrow

• question_answer3)
  The lengths of the sides of a triangle is x, y mid z respectively. If \[{{\mathbf{x}}^{\mathbf{2}}}\mathbf{+}{{\mathbf{y}}^{\mathbf{2}}}\mathbf{+}{{\mathbf{z}}^{\mathbf{2}}}\mathbf{=xy+yz+xz,}\] then the triangle is:
  A)
   Isosceles                       done clear
  B)
   Equilateral done clear
  C)
   Scalene                        done clear
  D)
   Right - angled done clear
  View Solution play_arrow

• question_answer4)
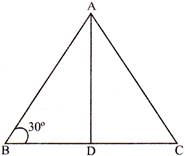
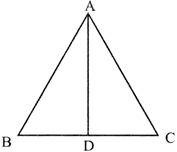
  In the figure given below, ABC is an isosceles triangle such that \[\mathbf{AB}=\mathbf{AC}\] and\[\angle \mathbf{B}=\mathbf{3}{{\mathbf{0}}^{{}^\circ }}\], AD is the median to the base BC. Then \[\Delta \mathbf{BAD}\] is:
  A)
   \[{{80}^{{}^\circ }}\]                        done clear
  B)
   \[{{40}^{{}^\circ }}\] done clear
  C)
   \[{{110}^{{}^\circ }}\]                                   done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer5)
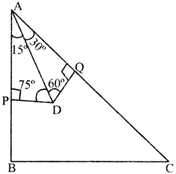
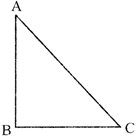
  In the figure given below, an isosceles triangle ABC is right angled at B. D is a point inside the triangle ABC. P and Q are the point of the perpendiculars drawn from D on the side AB and AC respectively of \[\Delta \mathbf{ABC}\]. If \[AP=x\] cm, \[\mathbf{AQ=y}\] cm and \[\angle \mathbf{BAD}=\mathbf{1}{{\mathbf{5}}^{{}^\circ }}\]. Then, sin\[{{75}^{{}^\circ }}=\]?
  A)
   \[\frac{2y}{\sqrt{3x}}\]             done clear
  B)
   \[\frac{x}{2y}\] done clear
  C)
   \[\frac{\sqrt{3x}}{2y}\] done clear
  D)
   \[\frac{2x}{\sqrt{3}y}\] done clear
  View Solution play_arrow

• question_answer6)
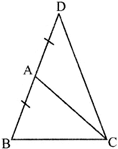
  In the given figure below, ABC is ail isosceles triangle with. The side BA Is produced to D such that \[\mathbf{AB}=\mathbf{AD}\]. If \[\angle ABC={{35}^{{}^\circ }}\], then \[\angle \mathbf{BCD}\] is equal to
  A)
   \[{{45}^{{}^\circ }}\]                        done clear
  B)
   \[{{90}^{{}^\circ }}\]           done clear
  C)
   \[{{30}^{{}^\circ }}\]                                    done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer7)
  In the given figure below. \[\Delta \mathbf{PQR}\] is an Isosceles triangle inscribed in a circle. If \[\mathbf{PQ=PR=12}\sqrt{\mathbf{5}}\]cm \[\mathbf{QR=24}\]cm then the radius of circle is
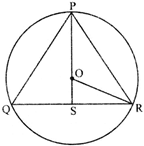
  A)
   10 cm              done clear
  B)
   15 cm done clear
  C)
   12 cm              done clear
  D)
   14 cm done clear
  View Solution play_arrow

• question_answer8)
  In the given figure below, \[\Delta \mathbf{ABC}\] is an isosceles triangle with \[\mathbf{AB}=\mathbf{AC}=\mathbf{17}\]cm and altitude from A to BC is 15 cm. The length of side BC is:
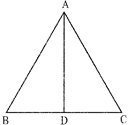
  A)
   9 cm                            done clear
  B)
   12 cm          done clear
  C)
   16 cm    done clear
  D)
   20 cm done clear
  View Solution play_arrow

• question_answer9)
  In the (not drawn to scale) given figure below, if \[\mathbf{AD}=\mathbf{DC}=\mathbf{BC}\] and \[\angle \mathbf{BCE}=\mathbf{8}{{\mathbf{4}}^{{}^\circ }}\]then \[\angle \mathbf{DBC}\]is:                                                        
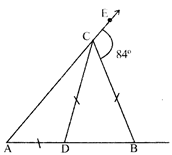
  A)
   \[{{64}^{{}^\circ }}\]                           done clear
  B)
   \[{{84}^{{}^\circ }}\] done clear
  C)
   \[{{56}^{{}^\circ }}\]   done clear
  D)
   \[{{96}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer10)
  In the given figure below, 0 and C are respectively the orthocentre and circum centre of an acute angled triangle PQR. The points P and 0 are joined and produced to meet the side QR at S. If \[\angle \mathbf{PQS}=\mathbf{6}{{\mathbf{0}}^{{}^\circ }}\]and \[\angle \mathbf{QCR}=\mathbf{13}{{\mathbf{0}}^{{}^\circ }}\], then \[\angle \mathbf{RPS}=\]
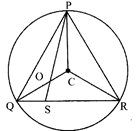
  A)
   \[{{30}^{{}^\circ }}\]                         done clear
  B)
   \[{{35}^{{}^\circ }}\] done clear
  C)
   \[{{100}^{{}^\circ }}\]                       done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer11)
  In the given figure below, the external bisector of \[\angle \mathbf{B}\] and \[\angle C\] of \[\Delta \mathbf{ABC}\] (where AB and AC extended to E and F respectively) meet at point P. If \[\angle \mathbf{BAC}=\mathbf{12}{{\mathbf{0}}^{{}^\circ }}\], then the measure of \[\angle \mathbf{BPC}\] is
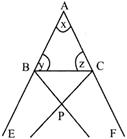
  A)
   \[{{50}^{{}^\circ }}\]                        done clear
  B)
   \[{{80}^{{}^\circ }}\]             done clear
  C)
   \[{{30}^{{}^\circ }}\]  done clear
  D)
   \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer12)
                    In a \[\Delta \mathbf{ABC},\overline{\mathbf{AD}},\overline{\mathbf{BE}}\], and \[\overline{\mathbf{CF}}\] are three medians. Then the ratio \[\left( {{\overline{\mathbf{AD}}}^{\mathbf{2}}}\mathbf{+}{{\overline{\mathbf{BE}}}^{\mathbf{2}}}\mathbf{+}{{\overline{\mathbf{CF}}}^{\mathbf{2}}} \right)\mathbf{:}\]\[\left( {{\overline{\mathbf{AB}}}^{\mathbf{2}}}\mathbf{+}{{\overline{\mathbf{AC}}}^{\mathbf{2}}}\mathbf{+}{{\overline{\mathbf{BC}}}^{\mathbf{2}}} \right)\] is
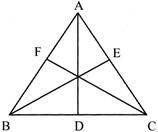
  A)
   Equal to \[\frac{3}{4}\]     done clear
  B)
   Equal to 1 done clear
  C)
   Greater than \[\frac{3}{4}\]         done clear
  D)
   Equal to \[\frac{1}{2}\] done clear
  View Solution play_arrow

• question_answer13)
  In \[\Delta \mathbf{ABC},\angle \mathbf{B}=\mathbf{6}{{\mathbf{0}}^{{}^\circ }}\], and \[\angle \mathbf{C}=\mathbf{5}{{\mathbf{0}}^{{}^\circ }}\], AD and AE are respectively the bisector of \[\angle \mathbf{A}\] and perpendicular on BC. The measure of \[\angle \mathbf{EAD}\] is:
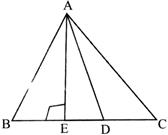
  A)
   \[{{11}^{{}^\circ }}\]                         done clear
  B)
   \[{{5}^{{}^\circ }}\]  done clear
  C)
   \[{{12}^{{}^\circ }}\]                         done clear
  D)
   \[{{9}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer14)
  In the given figure below, G is the centroid of\[\Delta \mathbf{ABC}\]. If \[\mathbf{AG}=\mathbf{BC}\], then measure of \[\angle \mathbf{BGC}\] is
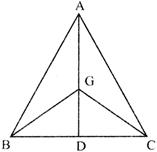
  A)
   \[{{45}^{{}^\circ }}\]                           done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\]   done clear
  D)
   \[{{120}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer15)
  In \[\Delta \mathbf{ABC}\], \[\mathbf{AB}=\mathbf{a}-\mathbf{b},\mathbf{AC}=\sqrt{{{\mathbf{a}}^{\mathbf{2}}}+{{\mathbf{b}}^{\mathbf{2}}}}\]and \[\mathbf{BC}=\sqrt{2\mathbf{ab}}\], then find single B.
  A)
   \[{{60}^{{}^\circ }}\]                                    done clear
  B)
   \[{{30}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\]     done clear
  D)
   \[{{45}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer16)
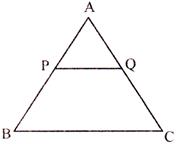
  In the given figure below, ABC is a triangle, PQ is line segment intersecting AB in P and AC in Q and \[\mathbf{PQ}\parallel \mathbf{BC}\]. The ratio of AP: BP = 2:5 and length of PQ is 18 cm. The length of BC is
  A)
   36 cm.                        done clear
  B)
   63 cm. done clear
  C)
   48 cm.                        done clear
  D)
   24 cm. done clear
  View Solution play_arrow

• question_answer17)
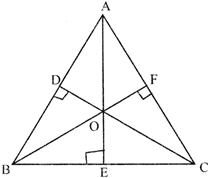
  In the given figure below, Let O be the orthocentre of the triangle ABC., If \[\angle \mathbf{BOC}=\mathbf{14}{{\mathbf{0}}^{{}^\circ }}\], Then \[\angle \mathbf{BAC}\] is
  A)
   \[{{40}^{{}^\circ }}\]   done clear
  B)
   \[{{50}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\]                                    done clear
  D)
   \[{{120}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer18)
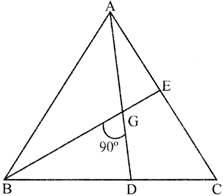
  in the given figure below two medians AD and BE of \[\Delta ABC\] intersect at G at right angles. If \[AD=18\]cm and \[\mathbf{BE=12}\]cm, then the length of BD (in cm) is
  A)
   10        done clear
  B)
   6 done clear
  C)
   5                                 done clear
  D)
   3 done clear
  View Solution play_arrow

• question_answer19)
  in \[\Delta ABC,\text{ }AD\bot BC\] and \[A{{D}^{2}}=BD.DC\] the measure of \[\angle BAC\] is.
  A)
   \[{{60}^{{}^\circ }}\]                         done clear
  B)
   \[{{75}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\] done clear
  D)
   \[{{45}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer20)
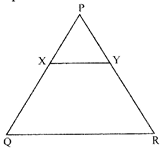
  In a \[\Delta \mathbf{ABC}\], X and Y are two points on PQ and PR respectively such that \[\mathbf{XY}\parallel \mathbf{QR}\], bisects the AABC in two equal areas. Then the ratio QX : PQ is
  A)
   \[1:\sqrt{2}\]                done clear
  B)
   1:2 done clear
  C)
   \[\left( \sqrt{2}-1 \right):\sqrt{2}\]    done clear
  D)
   \[\sqrt{2}:1\] done clear
  View Solution play_arrow

• question_answer21)
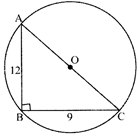
  Let ABC is triangle right angled at B. If AB = 12 cm and BC = 9 cm then what is the length of the circumradius of the \[\Delta \mathbf{ABC}\]?
  A)
   10 cm                          done clear
  B)
   7 cm           done clear
  C)
   6 cm                            done clear
  D)
   7.5 cm done clear
  View Solution play_arrow

• question_answer22)
  If AD is the internal angular bisector of \[\Delta \mathbf{ABC}\] with \[\mathbf{AB}=\mathbf{4}\]cm and \[\mathbf{AC}=\mathbf{1}\]cm, then what is BD : BC ?
  A)
   1 : 3                             done clear
  B)
   1 : 4              done clear
  C)
   5 : 4                             done clear
  D)
   4 : 5 done clear
  View Solution play_arrow

• question_answer23)
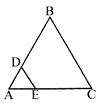
  If each side of triangle ABC is of length 4 and if AD is 1 and \[\mathbf{ED}\bot \mathbf{AB}\]. The area of region BCED is equal to
  A)
   \[8\sqrt{3}\]                  done clear
  B)
   \[4\sqrt{3}\] done clear
  C)
   \[4.5\sqrt{3}\]               done clear
  D)
   \[3.5\sqrt{3}\] done clear
  View Solution play_arrow

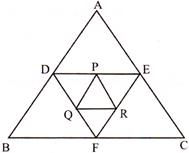
• question_answer24)
  A\[\Delta \mathbf{DEF}\] is formed by joining the mid-points of the sides of \[\Delta \mathbf{ABC}\]. Similarly, a \[\Delta \mathbf{DEF}\] is formed by joining the mid-points of the sides of the \[\Delta \mathbf{PQR}\]. If the sides of the \[\Delta \mathbf{PQR}\] are of lengths 2, 3 and 4 units, what is the perimeter of the\[\Delta \mathbf{ABC}\]?
  A)
   18 units                        done clear
  B)
   36 units done clear
  C)
   48 units                        done clear
  D)
   cannot be determined done clear
  View Solution play_arrow

• question_answer25)
  PQR is an equilateral triangle. O is the point of intersection of altitudes PL, QM RN, If \[\mathbf{OP}=\mathbf{9}\]cm, then what is the perimeter of the \[\Delta \mathbf{PQR}\]?
  A)
   \[6\sqrt{3}\]cm                          done clear
  B)
   \[12\sqrt{3}\]cm        done clear
  C)
   \[16\sqrt{3}\]cm           done clear
  D)
   \[18\sqrt{3}\]cm. done clear
  View Solution play_arrow

• question_answer26)
  ABC is a right angled triangle such that AB \[AB=\mathbf{x}-\mathbf{y},\mathbf{BC}=\mathbf{x}\] and \[\mathbf{CA}=\mathbf{x}-\mathbf{y}\], D is a point on BC such that \[BD=AB\]. The ratio of BD:DC for any value of x and y is given by
  A)
   3:2                               done clear
  B)
   4:3              done clear
  C)
   5:4                               done clear
  D)
   3:1 done clear
  View Solution play_arrow

• question_answer27)
  Let ABC be an equilateral triangle. If the side BC is produced to the point D so that \[BC=2CD\], then \[\mathbf{A}{{\mathbf{D}}^{\mathbf{2}}}\]is equal to
  A)
   \[3C{{D}^{2}}\]                     done clear
  B)
   \[4C{{D}^{2}}\]          done clear
  C)
   \[5C{{D}^{2}}\]                     done clear
  D)
   \[7C{{D}^{2}}\] done clear
  View Solution play_arrow

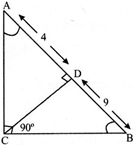
• question_answer28)
  In a \[\Delta \mathbf{ABC},\] \[\mathbf{BCA}=\mathbf{9}{{\mathbf{0}}^{{}^\circ }}\] and CD is perpendicular to AB If \[\mathbf{AD}=\mathbf{4}\]cm and \[\mathbf{BD}=\mathbf{9}\]cm, then the value of CD will be
  A)
   \[\sqrt{18}\] cm             done clear
  B)
   \[\sqrt{20}\] cm done clear
  C)
   8 cm                            done clear
  D)
   6 cm done clear
  View Solution play_arrow

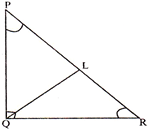
• question_answer29)
  In    the    adjoining    figure    given, \[\angle \mathbf{PQR}=\mathbf{9}{{\mathbf{0}}^{{}^\circ }}\]and QL is a median, \[\mathbf{PQ}=\mathbf{12}\]cm, and \[\mathbf{QR}=\mathbf{14}\]cm. Then, QL is equal to
  A)
   10cm    done clear
  B)
   5.5cm done clear
  C)
   6 cm                            done clear
  D)
   6.5 cm done clear
  View Solution play_arrow

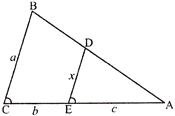
• question_answer30)
  Using the following figure\[\angle \mathbf{BCE}=\angle \mathbf{DEA}\], then determine x.
  A)
   \[\frac{ac}{b+c}\]         done clear
  B)
   \[\frac{ac}{b-c}\] done clear
  C)
   \[\frac{b+c}{ca}\]                     done clear
  D)
   \[\frac{2ac}{b+c}\] done clear
  View Solution play_arrow