Category : JEE Main & Advanced
(1) Cartesian co-ordinates : Let \[O\] be a fixed point, known as origin and let \[OX,OY\] and \[OZ\]be three mutually perpendicular lines, taken as x-axis, y-axis and z-axis respectively, in such a way that they form a right-handed system.
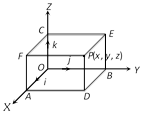
The planes \[XOY,YOZ\] and \[ZOX\]are known as xy-plane, yz-plane and zx-plane respectively.
Also,\[OA=x,\,\,OB=y,\,\,OC=z\].
The three co-ordinate planes (\[XOY,YOZ\] and\[ZOX\]) divide space into eight parts and these parts are called octants.
Sign of co-ordinates of a point : The signs of the co-ordinates of a point in three dimension follow the convention that all distances measured along or parallel to \[OX,\,\,OY,\,\,OZ\] will be positive and distances moved along or parallel to \[OX',\,\,OY',\,\,OZ'\] will be negative.

(2) Cylindrical co-ordinates : If the rectangular cartesian co-ordinates of \[P\] are \[(x,y,z),\] then those of \[N\] are \[(x,y,\text{ }0)\] and we can easily have the following relations : \[x=u\cos \,\phi ,\,\,y=u\sin \phi \] and \[z=z\].
Hence, \[{{u}^{2}}={{x}^{2}}+{{y}^{2}}\] and \[\varphi ={{\tan }^{-1}}(y/x)\].
Cylindrical co-ordinates of \[P\equiv (u,\phi ,z)\]
(3) Spherical polar co-ordinates : The measures of quantities \[r,\,\,\theta ,\,\,\phi \] are known as spherical or three dimensional polar co-ordinates of the point \[P\]. If the rectangular cartesian co-ordinates of \[P\] are \[(x,y,z)\] then \[z=r\cos \,\theta ,\,\,u=r\sin \,\theta \].
\[\therefore \] \[x=u\cos \,\phi =r\sin \,\theta \,\cos \,\phi ,\,\,y=u\sin \,\phi =r\,\sin \theta \,\sin \,\phi \] and \[z=r\cos \,\theta \]
Also, \[{{r}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}\]and \[\tan \theta =\frac{u}{z}=\frac{\sqrt{{{x}^{2}}+{{y}^{2}}}}{z};\,\,\tan \phi =\frac{y}{x}\].
You need to login to perform this action.
You will be redirected in
3 sec
