JEE Main & Advanced Mathematics Trigonometric Equations Question Bank

done Height and Distance Total Questions - 64

• question_answer1)
  The angle of elevation of the top of a tower at point on the ground is\[{{30}^{o}}\]. If on walking 20 metres toward the tower, the angle of elevation become\[{{60}^{o}}\], then the height of the tower is [MNR 1975; IIT 1967]
  A)
  10 metre done clear
  B)
  \[\frac{10}{\sqrt{3}}metre\] done clear
  C)
  \[10\sqrt{3}metre\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer2)
  The angle of elevation of a tower at a point distant d meters from its base is 30°. If the tower is  20 meters high, then the value of d is [MP PET 1982, 88]
  A)
  \[10\sqrt{3}m\] done clear
  B)
  \[\frac{20}{\sqrt{3}}m\] done clear
  C)
  \[20\sqrt{3}m\] done clear
  D)
  \[10\]m done clear
  View Solution play_arrow

• question_answer3)
  The angle of elevation of the top of the tower observed from each of the three points \[A,B,C\]on the ground, forming a triangle is the same angle \[\alpha \]. If R is the circum-radius of the triangle ABC, then the height of the tower is [EAMCET 1994]
  A)
  \[R\sin \alpha \] done clear
  B)
  \[R\cos \alpha \] done clear
  C)
  \[R\cot \alpha \] done clear
  D)
  \[R\tan \alpha \] done clear
  View Solution play_arrow

• question_answer4)
  The angle of elevation of the top of a tower from a point A due south of the tower is \[\alpha \]and from a point B due east of the tower is \[\beta \]. If AB =d, then the height of the tower is   [Roorkee 1979; Kurukshetra CEE 1998]
  A)
  \[\frac{d}{\sqrt{{{\tan }^{2}}\alpha -{{\tan }^{2}}\beta }}\] done clear
  B)
  \[\frac{d}{\sqrt{{{\tan }^{2}}\alpha +{{\tan }^{2}}\beta }}\] done clear
  C)
  \[\frac{d}{\sqrt{{{\cot }^{2}}\alpha +{{\cot }^{2}}\beta }}\] done clear
  D)
  \[\frac{d}{\sqrt{{{\cot }^{2}}\alpha -{{\cot }^{2}}\beta }}\] done clear
  View Solution play_arrow

• question_answer5)
  A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 40 meters from the bank, he finds the angle to be\[{{30}^{o}}\]. The breadth of the river is   [IIT 1975; AIEEE 2004]
  A)
  20 m done clear
  B)
  40 m done clear
  C)
  30 m done clear
  D)
  60 m done clear
  View Solution play_arrow

• question_answer6)
  A vertical pole consists of two parts, the lower part being one third of the whole. At a point in the horizontal plane through the base of the pole and distance 20 meters from it, the upper part of the pole subtends an angle whose tangent is \[\frac{1}{2}\]. The possible heights of the pole are [IIT 1964]
  A)
  20 m and \[20\sqrt{3}\,m\] done clear
  B)
  20 m and 60 m done clear
  C)
  16 m and 48 m done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer7)
  From a 60 meter high tower angles of depression of the top and bottom of a house are a and b respectively. If the height of the house is \[\frac{60\,\sin \,(\beta -\alpha )}{x},\] then x = 
  A)
  \[\sin \,\,\alpha \,\,\sin \,\,\beta \] done clear
  B)
  \[\cos \,\,\alpha \,\,\cos \,\,\beta \] done clear
  C)
  \[\sin \,\,\alpha \,\,\cos \,\,\beta \] done clear
  D)
  \[\cos \,\,\alpha \,\,\sin \,\,\beta \] done clear
  View Solution play_arrow

• question_answer8)
  An observer on the top of a tree, finds the angle of depression of a car moving towards the tree to be 30oo. After 3 minutes this angle becomes 60o. After how much more time, the car will reach the tree
  A)
  4 min. done clear
  B)
  4.5 min. done clear
  C)
  1.5 min. done clear
  D)
  2 min. done clear
  View Solution play_arrow

• question_answer9)
  A house of height 100 metres subtends a right angle at the window of an opposite house. If the height of the window be 64 metres, then the distance between the two houses is
  A)
  48 m done clear
  B)
  36 m done clear
  C)
  54 m done clear
  D)
  72 m done clear
  View Solution play_arrow

• question_answer10)
  The length of the shadow of a pole inclined at 10o to the vertical towards the sun is 2.05 metres, when the elevation of the sun is 38o. The length of the pole is [Roorkee 1976]
  A)
  \[\frac{2.05\,\,\sin \,\,{{38}^{o}}}{\sin \,{{42}^{o}}}\] done clear
  B)
  \[\frac{2.05\,\,\sin \,\,{{42}^{o}}}{\sin \,{{38}^{o}}}\] done clear
  C)
  \[\frac{2.05\,\,\cos \,\,{{38}^{o}}}{\cos \,\,{{42}^{o}}}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer11)
  The angle of elevation of the top of a tower from a point    20 metre away from its base is 45o. The height of the tower is [MP PET 1984, 89]
  A)
  10 m done clear
  B)
  20 m done clear
  C)
  40 m done clear
  D)
  \[20\sqrt{3}\] m done clear
  View Solution play_arrow

• question_answer12)
  The horizontal distance between two towers is 60 metres and the angular depression of the top of the first tower as seen from the top of the second, is 30o. If the height of the second tower be 150 metres, then the height of the first tower is
  A)
  \[150-60\sqrt{3}\,m\] done clear
  B)
  90 m done clear
  C)
  \[150-20\sqrt{3}\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer13)
  From the top of a light house 60 meters high with its base at the sea level, the angle of depression of a boat is 15o. The distance of the boat from the foot of light house is   [MNR 1988; IIT 1983; MP PET 1994, 2001; UPSEAT 2000]
  A)
  \[\left( \frac{\sqrt{3}-1}{\sqrt{3}+1} \right)\,60\,\,m\] done clear
  B)
  \[\left( \frac{\sqrt{3}+1}{\sqrt{3}-1} \right)\,60\,\,m\] done clear
  C)
  \[\left( \frac{\sqrt{3}+1}{\sqrt{3}-1} \right)\,\,\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer14)
  An observer in a boat finds that the angle of elevation of a tower standing on the top of a cliff is 60o and that of the top of cliff is 30o. If the height of the tower be 60 meters, then the height of the cliff is [Roorkee 1982]
  A)
  30 m done clear
  B)
  \[60\sqrt{3}\,\,m\] done clear
  C)
  \[20\sqrt{3}\,\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer15)
  A tower subtends an angle a  at a point A in the plane of its base and the angle of depression of the foot of the tower at a point l meters just above A is b. The height of the tower is    [MP PET 1990; RPET 1990]
  A)
  \[l\,\,\tan \,\beta \,\cot \,\alpha \] done clear
  B)
  \[l\,\,\tan \,\alpha \,\cot \,\beta \] done clear
  C)
  \[l\,\,\tan \,\,\alpha \,\,\tan \,\beta \] done clear
  D)
  \[l\,\,\cot \,\,\alpha \,\,\cot \,\beta \] done clear
  View Solution play_arrow

• question_answer16)
  The angle of elevation of a tower from a point A due south of it is 30o and from a point B due west of it is 45o. If the height of the tower be 100 metres, then AB =
  A)
  150 m done clear
  B)
  200 m done clear
  C)
  173.2 m done clear
  D)
  141.4 m done clear
  View Solution play_arrow

• question_answer17)
  An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60o and after 10 seconds the elevation is observed to be\[{{30}^{o}}\]. The uniform speed of the aeroplane in \[km/h\] is [IIT 1965]
  A)
  240 done clear
  B)
  \[240\sqrt{3}\] done clear
  C)
  \[60\sqrt{3}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer18)
  From a point a metre above a lake the angle of elevation of a cloud is a and the angle of depression of its reflection is b. The height of the cloud is [Roorkee 1983; EAMCET 1983, 85]
  A)
  \[\frac{a\sin \,(\alpha +\beta )}{\sin \,(\alpha -\beta )}\] metre done clear
  B)
  \[\frac{a\sin \,(\alpha +\beta )}{\sin \,(\beta -\alpha )}\] metre done clear
  C)
  \[\frac{a\sin \,(\beta -\alpha )}{\sin \,(\alpha +\beta )}\] metre done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer19)
  If the angle of depression of a point A on the ground from the top of a tower be\[{{30}^{o}}\], then the angle of elevation of the top of the tower from the point A will be
  A)
  \[{{60}^{o}}\] done clear
  B)
  \[{{45}^{o}}\] done clear
  C)
  \[{{30}^{o}}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer20)
  Two vertical poles of equal heights are 120 m apart. On the line joining their bottoms, A and B are two points. Angle of elevation of the top of one pole from A is 45o and that of the other pole from B is also 45o. If AB =  30 m, then the height of each pole is
  A)
  40 m done clear
  B)
  45 m done clear
  C)
  50 m done clear
  D)
  42 m done clear
  View Solution play_arrow

• question_answer21)
  At a distance 2h from the foot of a tower of height h, the tower and a pole at the top of the tower subtend equal angles. Height of the pole should be
  A)
  \[\frac{5h}{3}\] done clear
  B)
  \[\frac{4h}{3}\] done clear
  C)
  \[\frac{7h}{5}\] done clear
  D)
  \[\frac{3h}{2}\] done clear
  View Solution play_arrow

• question_answer22)
  A house subtends a right angle at the window of an opposite house and the angle of elevation of the window from the bottom of the first house is\[{{60}^{o}}\]. If the distance between the two houses be 6 metres, then the height of the first house is [MNR 1978]
  A)
  \[6\sqrt{3}\,\,m\] done clear
  B)
  \[8\sqrt{3}\,\,m\] done clear
  C)
  \[4\sqrt{3}\,\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer23)
  The angle of elevation of the sun, when the shadow of the pole is\[\sqrt{3}\]times the height of the pole, is  [MP PET 1991, 96]
  A)
  \[{{60}^{o}}\] done clear
  B)
  \[{{30}^{o}}\] done clear
  C)
  \[{{45}^{o}}\] done clear
  D)
  \[{{15}^{o}}\] done clear
  View Solution play_arrow

• question_answer24)
  A ladder rests against a wall so that its top touches the roof of the house. If the ladder makes an angle of\[{{60}^{o}}\]with the horizontal and height of the house be \[6\sqrt{3}\] meters, then the length of the ladder is
  A)
  \[12\sqrt{3}\] done clear
  B)
  12 m done clear
  C)
  \[12/\sqrt{3}\,\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer25)
  If the angles of elevation of two towers from the middle point of the line joining their feet be\[{{60}^{o}}\]and\[{{30}^{o}}\]respectively, then the ratio of their heights is  [EAMCET 1987]
  A)
  2 : 1 done clear
  B)
  \[1\,\,:\,\,\sqrt{2}\] done clear
  C)
  3 : 1 done clear
  D)
  \[1\,\,:\,\,\sqrt{3}\] done clear
  View Solution play_arrow

• question_answer26)
  At a point on the ground the angle of elevation of a tower is such that its cotangent is 3/5. On walking 32 metres towards the tower the cotangent of the angle of elevation is 2/5. The height of the tower is
  A)
  160 m done clear
  B)
  120 m done clear
  C)
  64 m done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer27)
  Some portion of a 20 meters long tree is broken by the wind and the top struck the ground at an angle of\[{{30}^{o}}\]. The height of the point where the tree is broken is  [MNR 1974]
  A)
  10 m done clear
  B)
  \[(2\sqrt{3}-3)\,20\,\,m\] done clear
  C)
  \[\frac{20}{3}m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer28)
  The base of a cliff is circular. From the extremities of a diameter of the base the angles of elevation of the top of the cliff are 30o and\[{{60}^{o}}\]. If the height of the cliff be 500 metres, then the diameter of the base of the cliff is
  A)
  \[1000\,\sqrt{3}\,m\] done clear
  B)
  \[2000/\sqrt{3}\,m\] done clear
  C)
  \[1000/\sqrt{3}\,m\] done clear
  D)
  \[2000\sqrt{2}\,m\] done clear
  View Solution play_arrow

• question_answer29)
  The angle of elevation of the top of a tower from the top of a house is\[{{60}^{o}}\]and the angle of depression of its base is\[{{30}^{o}}\]. If the horizontal distance between the house and the tower be 12 m, then the height of the tower is
  A)
  \[48\,\sqrt{3}\,\,m\] done clear
  B)
  \[16\,\sqrt{3}\,\,m\] done clear
  C)
  \[24\,\sqrt{3}\,\,m\] done clear
  D)
  \[16/\,\sqrt{3}\,\,m\] done clear
  View Solution play_arrow

• question_answer30)
  A man whose eye level is 1.5 metres above the ground observes the angle of elevation of a tower to be\[{{60}^{o}}\]. If the distance of the man from the tower be 10 meters, the height of the tower is
  A)
  \[(1.5+10\sqrt{3})\,m\] done clear
  B)
  \[10\,\sqrt{3}\,m\] done clear
  C)
  \[\left( 1.5+\frac{10}{\sqrt{3}} \right)\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer31)
  A tower subtends an angle of\[{{30}^{o}}\]at a point distant d from the foot of the tower and on the same level as the foot of the tower. At a second point h vertically above the first, the depression of the foot of the tower is\[{{60}^{o}}\]. The height of the tower is [MP PET 1993]
  A)
  h/3 done clear
  B)
  h/3d done clear
  C)
  3h done clear
  D)
  \[\frac{3h}{d}\] done clear
  View Solution play_arrow

• question_answer32)
  A tower of height b subtends an angle at a point O on the level of the foot of the tower and at a distance a from the foot of the tower. If a pole mounted on the tower also subtends an equal angle at O, the height of the pole is  [MP PET 1993, 2004]
  A)
  \[b\,\left( \frac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}} \right)\] done clear
  B)
  \[b\,\left( \frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}-{{b}^{2}}} \right)\] done clear
  C)
  \[a\,\left( \frac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}} \right)\] done clear
  D)
  \[a\,\left( \frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}-{{b}^{2}}} \right)\] done clear
  View Solution play_arrow

• question_answer33)
  A tree is broken by wind, its upper part touches the ground at a point 10 metres from the foot of the tree and makes an angle of\[{{45}^{o}}\]with the ground. The total length of tree is  [BIT Ranchi 1992]
  A)
  15 metres done clear
  B)
  20 metres done clear
  C)
  \[10\,(1+\sqrt{2})\]metres done clear
  D)
  \[10\,\left( 1+\frac{\sqrt{3}}{2} \right)\]metres done clear
  View Solution play_arrow

• question_answer34)
  The angle of depression of a ship from the top of a tower   30 metre high is\[{{60}^{o}}\], then the distance of ship from the base of tower is                             [MP PET 1988; Pb. CET 2003]
  A)
  30 m done clear
  B)
  \[30\,\sqrt{3}\,\,m\] done clear
  C)
  \[10\sqrt{3}\,m\] done clear
  D)
  10 m done clear
  View Solution play_arrow

• question_answer35)
  The angle of elevation of a stationary cloud from a point 2500 m above a lake is\[{{15}^{o}}\]and the angle of depression of its reflection in the lake is\[{{45}^{o}}\]. The height of cloud above the lake level is [IIT 1976]
  A)
  \[2500\,\sqrt{3}\,metres\] done clear
  B)
  2500 metres done clear
  C)
  \[500\,\sqrt{3}\,metres\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer36)
  From an aeroplane vertically over a straight horizontally road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be a and b, then the height in miles of aeroplane above the road is   [MNR 1986; UPSEAT 1999]
  A)
  \[\frac{\tan \alpha \,.\,\tan \beta }{\cot \alpha +\cot \beta }\] done clear
  B)
  \[\frac{\tan \alpha +\tan \beta }{\tan \alpha \,.\,\tan \beta }\] done clear
  C)
  \[\frac{\cot \alpha +\cot \beta }{\tan \alpha \,.\,\tan \beta }\] done clear
  D)
  \[\frac{\tan \alpha \,.\,\tan \,\beta }{\tan \alpha +\tan \beta }\] done clear
  View Solution play_arrow

• question_answer37)
  A balloon is observed simultaneously from three points A, B and C on a straight road directly under it. The angular elevation at B is twice and at C is thrice that of A. If the distance between A and B is 200 metres and the distance between B and C is 100 metres, then the height of balloon is given by [Roorkee 1989]
  A)
  50 metres done clear
  B)
  \[50\,\sqrt{3}\] metres done clear
  C)
  \[50\,\sqrt{2}\] metres done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer38)
  A vertical pole (more than 100 m high) consists of two portions, the lower being one-third of the whole. If the upper portion subtends an angle \[{{\tan }^{-1}}\frac{1}{2}\] at a point in a horizontal plane through the foot of the pole and distance 40 ft from it, then the height of the pole is [AMU 1981]
  A)
  100 ft done clear
  B)
  120 ft done clear
  C)
  150 ft done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer39)
  A flag-post 20m high standing on the top of a house subtends an angle whose tangent is \[\frac{1}{6}\] at a distance 70 m from the foot of the house. The height of the house is
  A)
  30 m done clear
  B)
  60 m done clear
  C)
  50 m done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer40)
  A balloon is coming down at the rate of 4 m/min. and its angle of elevation is 45o from a point on the ground which has been reduced to 30o after 10 minutes. Balloon will be on the ground at a distance of how many meters from the observer
  A)
  \[20\,\sqrt{3}\,m\] done clear
  B)
  \[20\,(3+\sqrt{3})\,m\] done clear
  C)
  \[10\,(3+\sqrt{3})\,m\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer41)
  A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is\[{{45}^{o}}\]. Then which of the following statements is correct [MP PET 1994]
  A)
  Breadth of the river is twice the height of the tower done clear
  B)
  Breadth of the river and the height of the tower are the same done clear
  C)
  Breadth of the river is half of the height of the tower done clear
  D)
  None of the above done clear
  View Solution play_arrow

• question_answer42)
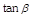
  AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3 AB. If C is the mid-point of AB and CB subtends an angle b at P, the value of  is [Bihar CEE 1994]
  A)
  \[\frac{18}{19}\] done clear
  B)
  \[\frac{3}{19}\] done clear
  C)
  \[\frac{1}{6}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer43)
  Two straight roads intersect at an angle of\[{{60}^{o}}\]. A bus on one road is 2 km away from the intersection and a car on the other road is 3 km away from the intersection. Then the direct distance between the two vehicles is  [BIT Ranchi 1993]
  A)
  1 km done clear
  B)
  \[\sqrt{2}\,\,km\] done clear
  C)
  4 km done clear
  D)
  \[\sqrt{7}\,\,km\] done clear
  View Solution play_arrow

• question_answer44)
   If a flagstaff of 6 metres high placed on the top of a tower throws a shadow of \[2\sqrt{3}\,metres\] along the ground, then the angle (in degrees) that the sun makes with the ground is  [EAMCET 1990]
  A)
  \[{{60}^{o}}\] done clear
  B)
  \[{{80}^{o}}\] done clear
  C)
  \[{{75}^{o}}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer45)
  The angle of elevation of a cliff at a point A on the ground and a point B, 100 m vertically at A are a and b respectively. The height of the cliff is [EAMCET 1986]
  A)
  \[\frac{100\,\,\cot \,\alpha }{\cot \alpha -\cot \beta }\] done clear
  B)
  \[\frac{100\,\,\cot \beta }{\cot \,\alpha -\cot \,\beta }\] done clear
  C)
  \[\frac{100\,\,\cot \beta }{\cot \beta -\cot \alpha }\] done clear
  D)
  \[\frac{100\,\,\cot \beta }{\cot \beta +\cot \alpha }\] done clear
  View Solution play_arrow

• question_answer46)
  A flag-staff of 5 m high stands on a building of 25 m high. At an observer at a height of 30 m. The flag-staff and the building subtend equal angles. The distance of the observer from the top of the flag-staff is [EAMCET 1993]
  A)
  \[\frac{5\sqrt{3}}{2}\] done clear
  B)
  \[5\sqrt{\frac{3}{2}}\] done clear
  C)
  \[5\sqrt{\frac{2}{3}}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer47)
  The upper part of a tree broken over by the wind makes an angle of\[{{30}^{o}}\]with the ground and the distance from the root to the point where the top of the tree touches the ground is 10 m; what was the height of the tree
  A)
  8.66 m done clear
  B)
  15 m done clear
  C)
  17.32 m done clear
  D)
  25.98 m done clear
  View Solution play_arrow

• question_answer48)
  The angle of depression of a point situated at a distance of 70 metres from the base of a tower is\[{{45}^{o}}\]. The height of the tower is [MP PET 1997]
  A)
  70 m done clear
  B)
  \[70\sqrt{2}\] m done clear
  C)
  \[\frac{70}{\sqrt{2}}m\] done clear
  D)
  35 m done clear
  View Solution play_arrow

• question_answer49)
  The angular elevation of a tower CD at a point A due south of it is\[{{60}^{o}}\]and at a point B due west of A, the elevation is\[{{30}^{o}}\]. If AB = 3 km, the height of the tower is [MP PET 1998]
  A)
  \[2\sqrt{3}\,km\] done clear
  B)
  \[2\sqrt{6}\,km\] done clear
  C)
  \[\frac{3\sqrt{3}}{2}km\] done clear
  D)
  \[\frac{3\sqrt{6}}{4}km\] done clear
  View Solution play_arrow

• question_answer50)
  A person is standing on a tower of height \[15(\sqrt{3}+1)\,m\] and observing a car coming towards the tower. He observed that angle of depression changes from\[{{30}^{o}}\]to\[{{45}^{o}}\]in 3 sec. What is the speed of the car [Karnataka CET 1998]
  A)
  36 km/hr done clear
  B)
  72 km/hr done clear
  C)
  18 km/hr done clear
  D)
  30 km/hr done clear
  View Solution play_arrow

• question_answer51)
  Two men are on the opposite side of a tower. They measure the angles of elevation of the top of the tower\[{{45}^{o}}\]and\[{{30}^{o}}\]respectively. If the height of the tower is 40 m, find the distance between the men [Karnataka CET 1998]
  A)
  40 m done clear
  B)
  \[40\sqrt{3}\,m\] done clear
  C)
  68.280 m done clear
  D)
  109.28 m done clear
  View Solution play_arrow

• question_answer52)
  The angles of elevation of the top of a tower  from the top  and bottom  at a building of height a are\[{{30}^{o}}\]and\[{{45}^{o}}\]respectively. If the tower and the building stand at the same level, then the height of the tower is     [Karnataka CET 2000]
  A)
  \[a\sqrt{3}\] done clear
  B)
  \[\frac{a\sqrt{3}}{\sqrt{3}-1}\] done clear
  C)
  \[\frac{a\,(3+\sqrt{3})}{2}\] done clear
  D)
  \[a\,(\sqrt{3}-1)\] done clear
  View Solution play_arrow

• question_answer53)
  A ladder 5 metre long leans against a vertical wall. The bottom of the ladder is 3 metre from the wall. If the bottom of the ladder is pulled 1 metre farther from the wall, how much does the top of the ladder slide down the wall [AMU 2000]
  A)
  1 m done clear
  B)
  7 m done clear
  C)
  2 m done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer54)
  The angle of elevation of the top of a pillar at any point A on the ground is\[{{15}^{o}}\]. On walking 40 metres towards the pillar, the angle become\[{{30}^{o}}\]. The height of the pillar is [MP PET 2001]
  A)
  40 metres done clear
  B)
  20 metres done clear
  C)
  \[20\sqrt{3}metres\] done clear
  D)
  \[\frac{40}{3}\sqrt{3}metres\] done clear
  View Solution play_arrow

• question_answer55)
  The top of a hill observed from the top and bottom of a building of height h is at the angle of elevation p and q respectively. The height of the hills is [UPSEAT 2001; EAMCET 1989]
  A)
  \[\frac{h\cot q}{\cot q-\cot p}\] done clear
  B)
  \[\frac{h\cot p}{\cot p-\cot q}\] done clear
  C)
  \[\frac{h\tan p}{\tan p-\tan q}\] done clear
  D)
  None of these done clear
  View Solution play_arrow

• question_answer56)
  The shadow of a tower standing on a level ground is found to be 60 m longer when the sun's altitude is\[{{30}^{o}}\]than when it is\[{{45}^{o}}\]. The height of the tower is [EAMCET 2001]
  A)
  60 m done clear
  B)
  30 m done clear
  C)
  \[60\sqrt{3}m\] done clear
  D)
  \[30(\sqrt{3}+1)m\] done clear
  View Solution play_arrow

• question_answer57)
  If the angle of elevation of the top of tower at a distance 500 m from its foot is\[{{30}^{o}}\], then height of the tower is   [Kerala (Engg.) 2002]
  A)
  \[\frac{1}{\sqrt{3}}\] done clear
  B)
  \[\frac{500}{\sqrt{3}}\] done clear
  C)
  \[\sqrt{3}\] done clear
  D)
  \[\frac{1}{500}\] done clear
  View Solution play_arrow

• question_answer58)
  For a man, the angle of elevation of the highest point of the temple situated east of him is\[{{60}^{o}}\]. On walking 240 metres to north, the angle of elevation is reduced to\[{{30}^{o}}\], then the height of the temple is [MP PET 2003]
  A)
  \[60\sqrt{6}m\] done clear
  B)
  \[60m\] done clear
  C)
  \[50\sqrt{3}m\] done clear
  D)
  \[30\sqrt{6}m\] done clear
  View Solution play_arrow

• question_answer59)
  20 metre high flag pole is fixed on a 80 metre high pillar,  50 metre away from it, on a point on the base of pillar the flag pole makes and angle \[\alpha \], then the value of \[\tan \alpha \], is  [MP PET 2003]
  A)
  \[\frac{2}{11}\] done clear
  B)
  \[\frac{2}{21}\] done clear
  C)
  \[\frac{21}{2}\] done clear
  D)
  \[\frac{21}{4}\] done clear
  View Solution play_arrow

• question_answer60)
  A tower subtends angles \[\alpha ,\,2\alpha ,\,3\alpha \]respectively at points A, B  and \[C\], all lying on a horizontal line through the foot of the tower. Then \[AB/BC=\]  [EAMCET 2003]
  A)
  \[\frac{\sin 3\alpha }{\sin 2\alpha }\] done clear
  B)
  \[1+2\cos 2\alpha \] done clear
  C)
  \[2+\cos 3\alpha \] done clear
  D)
  \[\frac{\sin 2\alpha }{\sin \alpha }\] done clear
  View Solution play_arrow

• question_answer61)
  Two pillars of equal height stand on either side of a roadway which is 60 metres wide. At a point in the roadway between the pillars, the elevation of the top of pillars are 60° and 30°. The height of the pillars is [UPSEAT 2004]
  A)
  \[15\sqrt{3}m\] done clear
  B)
  \[\frac{15}{\sqrt{3}}m\] done clear
  C)
  \[15m\] done clear
  D)
  \[20m\] done clear
  View Solution play_arrow

• question_answer62)
  A ladder rests against a wall making an angle \[\alpha \]with the horizontal. The foot of the ladder is pulled away from the wall through a distance x, so that it slides a distance y down the wall making an angle\[\beta \]with the horizontal. The correct relation is   [IIT 1985]
  A)
  \[x=y\tan \frac{\alpha +\beta }{2}\] done clear
  B)
  \[y=x\tan \frac{\alpha +\beta }{2}\] done clear
  C)
  \[x=y\tan (\alpha +\beta )\] done clear
  D)
  \[y=x\tan (\alpha +\beta )\] done clear
  View Solution play_arrow

• question_answer63)
  The shadow of a tower is found to be 60 metre shorter when the sun?s altitude changes from \[{{30}^{o}}\]to\[{{60}^{o}}\]. The height of the tower from the ground is approximately equal to  [Kerala (Engg.) 2005]
  A)
  62m done clear
  B)
  301m done clear
  C)
  101m done clear
  D)
  75m done clear
  E)
  52m done clear
  View Solution play_arrow

• question_answer64)
  \[ABCD\] is a rectangular field. A vertical lamp post of height 12m stands at the corner A. If the angle of elevation of its top from B is \[{{60}^{o}}\] and from C is\[{{45}^{o}}\], then the area of the field is [Kerala (Engg.) 2005]
  A)
  \[48\sqrt{2}sq.m\] done clear
  B)
  \[48\sqrt{3}sq.m\] done clear
  C)
  \[48sq.m\] done clear
  D)
  \[12\sqrt{2}sq.m\] done clear
  E)
  \[12\sqrt{3}sq.m\] done clear
  View Solution play_arrow