-
question_answer1) Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to A and T, respectively. At time t = 0 one particle has displacement A while the other one has displacement \[\frac{-A}{2}\]and they are moving towards each other If they cross each at time t, then t is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{T}{4}\]
done
clear
B)
\[\frac{5T}{6}\]
done
clear
C)
\[\frac{T}{3}\]
done
clear
D)
\[\frac{T}{6}\]
done
clear
View Answer play_arrow
-
question_answer2)
To find the focal length of a convex mirror, a student records the following data :
| Object pin |
Convex Lens |
Convex Mirror |
Image Pin |
| 22.2 cm |
32.2 cm |
45.8 cm |
71.2 cm |
The focal length of the convex lens is\[{{f}_{1}}\] and that of mirror is \[{{f}_{2}}.\]Then taking index correction to be negligibly small, \[{{f}_{1}}\]and \[{{f}_{2}}.\] are close to :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[{{f}_{1}}=15.6cm\] \[{{f}_{2}}=25.4cm\]
done
clear
B)
\[{{f}_{1}}=7.8cm\] \[{{f}_{2}}=12.7cm\]
done
clear
C)
\[{{f}_{1}}=7.8cm\] \[{{f}_{2}}=25.4cm\]
done
clear
D)
\[{{f}_{1}}=12.7cm\] \[{{f}_{2}}=7.8cm\]
done
clear
View Answer play_arrow
-
question_answer3)
Figure shows elliptical path abcd of a planet around the sun S such that the area of triangle csa is\[\frac{1}{4}\]the area of the ellipse . (See figure) With db as the semi major axis, and ca as the semi minor axis. If \[{{t}_{1}}\]is the time taken for planet to go over path abc and \[{{t}_{2}}\]for path taken over cda then : 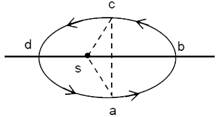 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
A)
\[{{t}_{1}}=3{{t}_{2}}\]
done
clear
B)
\[{{t}_{1}}={{t}_{2}}\]
done
clear
C)
\[{{t}_{1}}=2{{t}_{2}}\]
done
clear
D)
\[{{t}_{1}}=4{{t}_{2}}\]
done
clear
View Answer play_arrow
-
question_answer4) A simple pendulum made of a bob of mass m and a metallic wire of negligible mass has time period 2s at T = 0°C. If the temperature of the wire is increased and the corresponding charge in its time period is plotted against its temperature, the resulting graph is a line of slop S. If the coefficient of linear expansion of metal is a then the value of S is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{1}{\alpha }\]
done
clear
B)
\[2\alpha \]
done
clear
C)
\[\frac{\alpha }{2}\]
done
clear
D)
\[\alpha \]
done
clear
View Answer play_arrow
-
question_answer5) The ratio of work done by an ideal monatomic gas to the heat supplied to it in an isobaric process is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{3}{2}\]
done
clear
B)
\[\frac{2}{3}\]
done
clear
C)
\[\frac{3}{5}\]
done
clear
D)
\[\frac{2}{5}\]
done
clear
View Answer play_arrow
-
question_answer6) An unknown transistor needs to be identified as npn or pnp type .A multi meter, with +ve and .ve terminals, is used to measure resistance between different terminals transistor. If terminal 2 is the base of the transistor then which of the following is correct for a pnp transistor?
JEE Main Online Paper (Held On 09 April 2016)
A)
+ve terminal 3, .ve terminal 2, resistance high
done
clear
B)
+ve terminal 2, .ve terminal 3, resistance low
done
clear
C)
+ve terminal 1, .ve terminal 2, resistance high
done
clear
D)
+ve terminal 2, .ve terminal 1, resistance high
done
clear
View Answer play_arrow
-
question_answer7) A uniformly tapering conical wire is made from a material of Young's modulus Y and has a normal, un extended length L. The radii, at the upper and lower ends of this conical wire , have values R and 3R, respectively, The upper end of the wire is fixed to a rigid support and a mass M is suspended from its lower and . The equilibrium extended length, of this wire, would equal
JEE Main Online Paper (Held On 09 April 2016)
A)
\[L\left( 1+\frac{1}{3}\frac{Mg}{\pi Y{{R}^{2}}} \right)\]
done
clear
B)
\[L\left( 1+\frac{2}{3}\frac{Mg}{\pi Y{{R}^{2}}} \right)\]
done
clear
C)
\[L\left( 1+\frac{1}{9}\frac{Mg}{\pi Y{{R}^{2}}} \right)\]
done
clear
D)
\[L\left( 1+\frac{2}{9}\frac{Mg}{\pi Y{{R}^{2}}} \right)\]
done
clear
View Answer play_arrow
-
question_answer8)
A cubical block of side 30cm is moving with velocity \[2m{{s}^{-1}}\]on a smooth horizontal surface. The surface has a bump ata point O as shown in figure. The angular velocity (in rad/s) of the block immediately after it hits the bump, is : 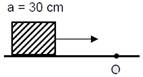 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
A)
9.4
done
clear
B)
6.7
done
clear
C)
5.0
done
clear
D)
13.3
done
clear
View Answer play_arrow
-
question_answer9) In Young's double slit experiment, the distance between slits and the screen is 1.0 m and monochromatic light of 600 nm is being used. A person standing near the slits is looking at the fringe pattern . When the separation between the slits is varied, the interference pattern disappears for a particular distance \[{{d}_{0}}\] between the slits. If the angular resolution of the eye is\[\frac{{{1}^{o}}}{60}\]the value of \[{{d}_{0}}\] is close to
JEE Main Online Paper (Held On 09 April 2016)
A)
2 mm
done
clear
B)
1 mm
done
clear
C)
3 mm
done
clear
D)
4 mm
done
clear
View Answer play_arrow
-
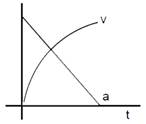
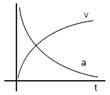
question_answer10) Which of the following option correctly describes the variation of the speed v and acceleration 'a' of a point mass falling vertically in a viscous medium that applies a force F = -kv, where 'k' is constant , on the body ? (Graphs are schematic and not drawn to scale)
JEE Main Online Paper (Held On 09 April 2016)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
-
question_answer11) A series LR circuit is connected to a voltage source with \[V(t)={{V}_{0}}\sin \Omega t.\]After very large time current I (t) behaves as \[\left( {{t}_{0}}>>\frac{L}{r} \right):\]
JEE Main Online Paper (Held On 09 April 2016)
A)
I (t)

B)
l (t)

C)
I (t)
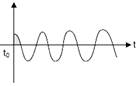
D)
l (t)
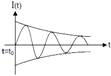
-
question_answer12) A car of weight W is on an inclined road that rises by 100 m over a distance of 1km and applies a constant frictional force \[\frac{W}{20}\] on the car. While moving uphill on the road at a speed of \[10m{{s}^{-1}},\]the car needs power \[\frac{P}{2}\]If it needs power while moving downhill at speed v then value of v is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[5\,m{{s}^{-1}}\]
done
clear
B)
\[20\,m{{s}^{-1}}\]
done
clear
C)
\[10\,m{{s}^{-1}}\]
done
clear
D)
\[15\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
-
question_answer13) A rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the rocket, making an angle \[\theta \]. With the horizontal , a point object of mass m is kept. The minimum coefficient of friction \[{{\mu }_{\min }}\] between the mass and the inclined surface such that he mass does not move is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\tan \theta \]
done
clear
B)
\[\tan 2\theta \]
done
clear
C)
\[3\tan \theta \]
done
clear
D)
\[2\tan \theta \]
done
clear
View Answer play_arrow
-
question_answer14) Two engines pass each other moving in opposite directions with uniform speed of 30m/s. One of them is blowing a whistle of frequency 540 Hz. Calculate the frequency heard by driver of second engine before pass each other. Speed sound is 330 m/sec.
JEE Main Online Paper (Held On 09 April 2016)
A)
540 Hz
done
clear
B)
648 Hz
done
clear
C)
270 Hz
done
clear
D)
450 Hz
done
clear
View Answer play_arrow
-
question_answer15) The potential (in volts) of a charge distribution is given by \[V(z)=30-5{{z}^{2}}\]for\[|z|\le 1m\] \[V(z)=35-10|z|\]for\[|z|\ge 1m.\] V(z) does not depend on x and y . If this potential is generated by a constant charge per unit volume \[{{\rho }_{0}},\](in units of \[{{\varepsilon }_{0}}\]) which is spread over certain region ,then choose the correct statement.
JEE Main Online Paper (Held On 09 April 2016)
A)
\[{{\rho }_{0}}=40{{\varepsilon }_{0}}\]in the entire region
done
clear
B)
\[{{\rho }_{0}}=20{{\varepsilon }_{0}}\] in the entire region
done
clear
C)
\[{{\rho }_{0}}=20{{\varepsilon }_{0}}\] for \[|z|\]in\[\le 1m\]and \[{{\rho }_{0}}=0\]else where
done
clear
D)
\[{{\rho }_{0}}=10{{\varepsilon }_{0}}\]for \[|z|\]in \[\le 1m\]and\[{{\rho }_{0}}=0\] else where
done
clear
View Answer play_arrow
-
question_answer16) An audio signal consists of two distinct sound : one a human speech signal in the frequency band of 200 Hz to 2700 Hz, while the other is a high frequency music signal in the frequency band of 10200 Hz to 15200 Hz. The ratio of the AM signal band width required to send both the signals together to the AM signal band width required to send just the human speech is :
JEE Main Online Paper (Held On 09 April 2016)
A)
6
done
clear
B)
5
done
clear
C)
3
done
clear
D)
2
done
clear
View Answer play_arrow
-
question_answer17)
A convex lens, of focal length 30cm, a concave lens of focal length 120 cm, and a plane mirror are arranged as shown. For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination, is a real image, at a distance of : 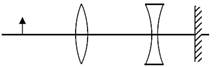 Focal length| |Focal length| = 30 cm =120 cm
Focal length| |Focal length| = 30 cm =120 cm 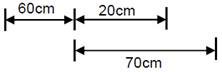 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
A)
70 cm from the concave lens
done
clear
B)
60 cm from the convex lens
done
clear
C)
60 cm from the concave lens
done
clear
D)
70 cm from the convex lens
done
clear
View Answer play_arrow
-
question_answer18) Three capacitors each of \[4\mu F\]are to be connected in such a way that the effective capacitance is \[6\mu F.\] This can be done by connecting them :
JEE Main Online Paper (Held On 09 April 2016)
A)
all in series
done
clear
B)
two in parallel and one in series
done
clear
C)
two in series and one in parallel
done
clear
D)
all in parallel
done
clear
View Answer play_arrow
-
question_answer19) To know the resistance G of a galvanometer by half deflection method, a battery of emf \[{{V}_{E}}\] and resistance R is used to deflect the galvanometer by angle\[\theta .\]If a shunt of resistance S is needed to gat half deflection then G, R and S are related by the equation :
JEE Main Online Paper (Held On 09 April 2016)
A)
2S = G
done
clear
B)
2G = S
done
clear
C)
S(R+G) = RG
done
clear
D)
2S(R+G) = RG
done
clear
View Answer play_arrow
-
question_answer20)
In the circuit shown, the resistance r is a variable resistance. If for r = fR, the heat generation in r is maximum then the value of f is : 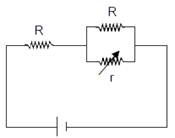 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
A)
1
done
clear
B)
\[\frac{3}{4}\]
done
clear
C)
\[\frac{1}{4}\]
done
clear
D)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
-
question_answer21) A hydrogen atom makes a transition from n = 2 to n=1 and emits a photon. This photon strikes a doubly ionized lithium atom (z = 3) in excited state and completely removes the orbiting electron. The least quantum number for the excited stated of the ion for the process is :
JEE Main Online Paper (Held On 09 April 2016)
A)
4
done
clear
B)
5
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
-
question_answer22) 200 g water is heated from \[40{}^\circ C\] to \[60{}^\circ C\]. Ignoring the slight expansion of water, the change in its internal energy is closed to (Given specific heat of water = 4184 J/kg/K) :
JEE Main Online Paper (Held On 09 April 2016)
A)
16.7 kJ
done
clear
B)
167.4kJ
done
clear
C)
4.2 kJ
done
clear
D)
8.4 kJ
done
clear
View Answer play_arrow
-
question_answer23) An experiment is performed to determine the I - V characteristics of a Zener diode, which has a protective resistance of \[R=100\Omega ,\]and maximum power of dissipation rating of 1W. The minimum voltage range of the DC source in the circuit is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[0.12V\]
done
clear
B)
\[0.5V\]
done
clear
C)
\[0.24\]
done
clear
D)
\[0 . 8V\]
done
clear
View Answer play_arrow
-
question_answer24) Microwave oven acts on the principle of :
JEE Main Online Paper (Held On 09 April 2016)
A)
giving rotational energy to water molecules
done
clear
B)
giving vibrational energy to water molecules
done
clear
C)
giving translational energy to water molecules
done
clear
D)
transferring electrons from lower to higher energy levels in water molecule
done
clear
View Answer play_arrow
-
question_answer25) A magnetic dipole is acted upon by two magnetic fields which are inclined to each other a tan angle of \[75{}^\circ \]. One of the fields has magnitude of 15mT. The dipole attains stable equilibrium at an angle \[30{}^\circ \] with this field. The magnitude of the other field (in mT) is close to :
JEE Main Online Paper (Held On 09 April 2016)
A)
11
done
clear
B)
1060
done
clear
C)
36
done
clear
D)
1
done
clear
View Answer play_arrow
-
question_answer26) \[A50\Omega \]resistance is connected to a battery of 5V. A galvanometer of resistance \[100\Omega \]is to be used as ammeter to measure current through the resistance, for this a resistance \[{{r}_{s}}\] is connected to the galvanometer. Which of the following connections should be employed if the measured current is within 1% of the current without the ammeter in the circuit ?
JEE Main Online Paper (Held On 09 April 2016)
A)
\[{{r}_{s}}=0.5\Omega n\]parallel with the galvanometer
done
clear
B)
\[{{r}_{s}}=0.5\Omega \]in series with the galvanometer
done
clear
C)
\[{{r}_{s}}=1\Omega \] in series with galvanometer
done
clear
D)
\[{{r}_{s}}=1\Omega \] in parallel with galvanometer
done
clear
View Answer play_arrow
-
question_answer27) When photons of wavelength \[{{\lambda }_{1}}\], are incident on an isolated sphere, the corresponding stopping potential is found to be V. When photons of wavelength \[{{\lambda }_{2}}\]are used , the corresponding stopping potential was thrice that of the above value. If light of wavelength \[{{\lambda }_{3}}.\]is used then find the stopping potential for this case
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{hc}{e}\left[ \frac{1}{{{\lambda }_{3}}}+\frac{1}{2{{\lambda }_{2}}}-\frac{3}{2{{\lambda }_{1}}} \right]\]
done
clear
B)
\[\frac{hc}{e}\left[ \frac{1}{{{\lambda }_{3}}}+\frac{1}{{{\lambda }_{2}}}-\frac{3}{{{\lambda }_{1}}} \right]\]
done
clear
C)
\[\frac{hc}{e}\left[ \frac{1}{{{\lambda }_{3}}}+\frac{1}{2{{\lambda }_{2}}}-\frac{1}{{{\lambda }_{1}}} \right]\]
done
clear
D)
\[\frac{hc}{e}\left[ \frac{1}{{{\lambda }_{3}}}-\frac{1}{{{\lambda }_{2}}}-\frac{1}{{{\lambda }_{1}}} \right]\]
done
clear
View Answer play_arrow
-
question_answer28) In the following 'I' refers to current and other symbols have their usual meaning choose the option that corresponds to the dimensions of electrical conductivity :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[{{M}^{-1}}{{L}^{-3}}{{T}^{3}}{{I}^{2}}\]
done
clear
B)
\[{{M}^{-1}}{{L}^{3}}{{T}^{3}}I\]
done
clear
C)
\[M{{L}^{-3}}{{T}^{-3}}{{I}^{2}}\]
done
clear
D)
\[{{M}^{-1}}{{L}^{-3}}{{T}^{3}}I\]
done
clear
View Answer play_arrow
-
question_answer29)
Consider a water jar of radius R that has water filled up to height H and is kept on a stand of height h (see figure). Through a hole of radius r (r<<R) at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is x. Then : 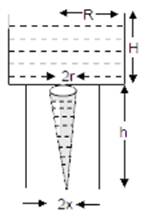 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
A)
\[x=r{{\left( \frac{H}{H+h} \right)}^{2}}\]
done
clear
B)
\[x=r\left( \frac{H}{H+h} \right)\]
done
clear
C)
\[x=r{{\left( \frac{H}{H+h} \right)}^{\frac{1}{4}}}\]
done
clear
D)
\[x=r{{\left( \frac{H}{H+h} \right)}^{\frac{1}{2}}}\]
done
clear
View Answer play_arrow
-
question_answer30)
The truth table given in fig. represents :
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
JEE Main Online Paper (Held On 09 April 2016)
A)
AND - Gate
done
clear
B)
OR - Gate
done
clear
C)
NOR - Gate
done
clear
D)
NAND - Gate
done
clear
View Answer play_arrow
-
question_answer31) The artificial sweetener that has the highest sweetness value in comparison to cane sugar is :
JEE Main Online Paper (Held On 09 April 2016)
A)
Saccharin
done
clear
B)
Sucralose
done
clear
C)
Alitame
done
clear
D)
Aspartane
done
clear
View Answer play_arrow
-
question_answer32) The non-metal that does not exhibit positive oxidation state is :
JEE Main Online Paper (Held On 09 April 2016)
A)
Fluorine
done
clear
B)
Oxygen
done
clear
C)
Chlorine
done
clear
D)
Iodine
done
clear
View Answer play_arrow
-
question_answer33)
The reaction of ozone with oxygen atoms in the presence of chlorine atoms can occur by a two step process show below:
|
\[{{O}_{3}}(g)+C{{l}^{\bullet }}(g)\to {{O}_{2}}(g)+Cl{{O}^{\bullet }}(g)\]……(i)
|
|
\[{{k}_{i}}=5.2\times {{10}^{9}}L\,mo{{l}^{-1}}{{s}^{-1}}\]
|
|
\[Cl{{O}^{\bullet }}(g)+{{O}^{\bullet }}(g)\to {{O}_{2}}(g)+C{{l}^{\bullet }}(g)\]……(ii)
|
|
\[{{k}_{ii}}=2.6\times {{10}^{10}}L\,mo{{l}^{-1}}{{s}^{-1}}\]
|
The closest rate constant for the overall reaction\[{{O}_{3}}(g)+{{O}^{\bullet }}(g)\to 2{{O}_{2}}(g)\] is:
JEE Main Online Paper (Held On 09 April 2016)
A)
\[1.4\times {{10}^{20}}L\,mo{{l}^{-1}}\,{{s}^{-1}}\]
done
clear
B)
\[5.2\times {{10}^{9}}L\,mo{{l}^{-1}}\,{{s}^{-1}}\]
done
clear
C)
\[3.1\times {{10}^{10}}L\,mo{{l}^{-1}}\,{{s}^{-1}}\]
done
clear
D)
\[2.6\times {{10}^{10}}L\,mo{{l}^{-1}}\,{{s}^{-1}}\]
done
clear
View Answer play_arrow
-
question_answer34) 5L of an alkane requires 25 L of oxygen for its complete combustion. If all volumes are measured at constant temperature and pressure, the alkane is:
JEE Main Online Paper (Held On 09 April 2016)
A)
Butane
done
clear
B)
Isobutane
done
clear
C)
Ethane
done
clear
D)
Propane
done
clear
View Answer play_arrow
-
question_answer35)
Match the items in Column I with its main use listed in Column II:
| Column I |
Column II |
| (a) Silica gel |
(i) Transistor |
| (b) Silicon |
(ii) Ion-exchanger |
| (c) Silicone |
(iii) Drying agent |
| (d) Silicate |
(iv) Sealant |
JEE Main Online Paper (Held On 09 April 2016)
A)
(A)-(iii), (B)-(i), (C)-(iv), (D)-(ii)
done
clear
B)
(A)-(ii), (B)-(i), (C)-(iv), (D)-(iii)
done
clear
C)
(A)-(iv), (B)-(i), (C)-(ii), (D)-(iii)
done
clear
D)
(A)-(ii), (B)-(iv), (C)-(i), (D)-(iii)
done
clear
View Answer play_arrow
-
question_answer36) The group of molecules having identical shape is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[PC{{l}_{5}},I{{F}_{5}},Xe{{O}_{2}}{{F}_{2}}\]
done
clear
B)
\[B{{F}_{3}},PC{{l}_{3}},Xe{{O}_{3}}\]
done
clear
C)
\[Cl{{F}_{3}},XeO{{F}_{2}},XeF_{3}^{+}\]
done
clear
D)
\[S{{F}_{4}},Xe{{F}_{4}},CC{{l}_{4}}\]
done
clear
View Answer play_arrow
-
question_answer37) Which one of the following species is stable in aqueous solution?
JEE Main Online Paper (Held On 09 April 2016)
A)
\[MnO_{4}^{2-}\]
done
clear
B)
\[MnO_{4}^{3-}\]
done
clear
C)
\[C{{u}^{+}}\]
done
clear
D)
\[C{{r}^{2+}}\]
done
clear
View Answer play_arrow
-
question_answer38) For the reaction, \[A(g)+B(g)\to C(g)+D(g),\Delta {{H}^{0}}\]and\[\Delta {{S}^{0}}\] are, respectively,\[-29.8kJ\,mo{{l}^{-1}}\]and\[-0.100kJ\,{{K}^{-1}}mo{{l}^{-1}}\]at 298 K. The equilibrium constant for the reaction at 298 K is:
JEE Main Online Paper (Held On 09 April 2016)
A)
1
done
clear
B)
10
done
clear
C)
1.0 × 10.10
done
clear
D)
1.0 × 1010
done
clear
View Answer play_arrow
-
question_answer39) Assertion : Rayon is a semisynthetic polymer whose properties are better than natural cotton. Reason : Mechanical and aesthetic properties of cellulose can be improved by acetylation.
JEE Main Online Paper (Held On 09 April 2016)
A)
Both assertion and reason are correct, and the reason is the correct explanation for the assertion.
done
clear
B)
Both assertion and reason are incorrect.
done
clear
C)
Assertion is incorrect statement, but the reason is correct.
done
clear
D)
Both assertion and reason are correct, but the reason is not the correct explanation for the assertion.
done
clear
View Answer play_arrow
-
question_answer40) The hydrocarbon with seven carbon atoms containing a neopentyl and a vinyl group is :
JEE Main Online Paper (Held On 09 April 2016)
A)
4,4-dimethylpentene
done
clear
B)
2,2-dimethyl-4-pentene
done
clear
C)
Isopropyl-2-butene
done
clear
D)
2,2-dimethyl-3-pentene
done
clear
View Answer play_arrow
-
question_answer41) The gas evolved on heating \[C{{H}_{3}}MgBr\]in methanol is:
JEE Main Online Paper (Held On 09 April 2016)
A)
Propane
done
clear
B)
Ethane
done
clear
C)
HBr
done
clear
D)
Methane
done
clear
View Answer play_arrow
-
question_answer42) Identify the correct trend given below: (Atomic No.: Ti = 22, Cr = 24 and Mo = 42)
JEE Main Online Paper (Held On 09 April 2016)
A)
\[{{\Delta }_{o}}\]of\[{{[Cr{{({{H}_{2}}O)}_{6}}]}^{2+}}<{{[Mo{{({{H}_{2}}O)}_{6}}]}^{2+}}\]and\[{{\Delta }_{o}}\]of\[{{[Ti{{({{H}_{2}}O)}_{6}}]}^{3+}}>{{[Ti{{({{H}_{2}}O)}_{6}}]}^{2+}}\]
done
clear
B)
\[{{\Delta }_{o}}\]of\[{{[Cr{{({{H}_{2}}O)}_{6}}]}^{2+}}>{{[Mo{{({{H}_{2}}O)}_{6}}]}^{2+}}\]and\[{{\Delta }_{o}}\]of\[{{[Ti{{({{H}_{2}}O)}_{6}}]}^{3+}}<{{[Ti{{({{H}_{2}}O)}_{6}}]}^{2+}}\]
done
clear
C)
\[{{\Delta }_{o}}\]of\[{{[Cr{{({{H}_{2}}O)}_{6}}]}^{2+}}>{{[Mo{{({{H}_{2}}O)}_{6}}]}^{2+}}\]and \[{{\Delta }_{o}}\]of\[{{[Ti{{({{H}_{2}}O)}_{6}}]}^{3+}}<{{[Ti{{({{H}_{2}}O)}_{6}}]}^{2+}}\]
done
clear
D)
\[{{\Delta }_{o}}\]of\[{{[Cr{{({{H}_{2}}O)}_{6}}]}^{2+}}<{{[Mo{{({{H}_{2}}O)}_{6}}]}^{2+}}\]and \[{{\Delta }_{o}}\]of\[{{[Ti{{({{H}_{2}}O)}_{6}}]}^{3+}}>{{[Ti{{({{H}_{2}}O)}_{6}}]}^{2+}}\]
done
clear
View Answer play_arrow
-
question_answer43) The most appropriate method of making egg-albumin sol is:
JEE Main Online Paper (Held On 09 April 2016)
A)
Keep the egg in boiling water for 10 minutes. After removing the shell, transfer the yellow part of the content to 100 mL of 5% w/V saline solution and homogenize with a mechanical shaker.
done
clear
B)
Break an egg carefully and transfer the transparent part of the content to 100 mL of 5% w/V saline solution and stir well.
done
clear
C)
Keep the egg in boiling water for 10 minutes. After removing the shell, transfer the white part of the content to 100 mL of 5% w/V saline solution and homogenize with a mechanical shaker.
done
clear
D)
Break an egg carefully and transfer only the yellow part of the content to 100 mL of 5% w/V saline solution and stir well.
done
clear
View Answer play_arrow
-
question_answer44) Which one of the following complexes will consume more equivalents of aqueous solution of \[Ag(N{{O}_{3}})\]?
JEE Main Online Paper (Held On 09 April 2016)
A)
\[N{{a}_{3}}[CrC{{l}_{6}}]\]
done
clear
B)
\[[Cr{{({{H}_{2}}O)}_{5}}Cl]C{{l}_{2}}\]
done
clear
C)
\[[Cr{{({{H}_{2}}O)}_{6}}]C{{l}_{3}}\]
done
clear
D)
\[[N{{a}_{2}}(CrC{{l}_{5}})({{H}_{2}}O)]\]
done
clear
View Answer play_arrow
-
question_answer45) At very high pressures, the compressibility factor of one mole of a gas is given by :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[1+\frac{pb}{RT}\]
done
clear
B)
\[\frac{pb}{RT}\]
done
clear
C)
\[1-\frac{b}{(VRT)}\]
done
clear
D)
\[1-\frac{pb}{RT}\]
done
clear
View Answer play_arrow
-
question_answer46) A reaction at 1 bar is non-spontaneous at low temperature but becomes spontaneous at high temperature. Identify the correct statement about the reaction among the following:
JEE Main Online Paper (Held On 09 April 2016)
A)
Both\[\Delta H\] and \[\Delta S\] are positive.
done
clear
B)
\[\Delta H\]is negative while \[\Delta S\] is positive.
done
clear
C)
\[\Delta H\]is positive while\[\Delta S\]is negative.
done
clear
D)
Both \[\Delta S\]and \[\Delta S\] are negative.
done
clear
View Answer play_arrow
-
question_answer47) Which intermolecular force is most responsible in allowing xenon gas to liquefy?
JEE Main Online Paper (Held On 09 April 2016)
A)
Instantaneous dipole-induced dipole
done
clear
B)
Ionic
done
clear
C)
Ion-dipole
done
clear
D)
Dipole-dipole
done
clear
View Answer play_arrow
-
question_answer48) Identify the incorrect statement regarding heavy water:
JEE Main Online Paper (Held On 09 April 2016)
A)
It reacts with \[Ca{{C}_{2}}\]to produce \[{{C}_{2}}{{D}_{2}}\] and \[Ca{{(OD)}_{2}}.\]
done
clear
B)
It is used as a coolant in nuclear reactors.
done
clear
C)
It reacts with \[A{{l}_{4}}{{C}_{3}}\] to produce \[C{{D}_{4}}\] and \[Al{{(OD)}_{3}}.\]
done
clear
D)
It reacts with \[S{{O}_{3}}\]to form deuterated sulphuric acid \[({{D}_{2}}S{{O}_{4}}).\]
done
clear
View Answer play_arrow
-
question_answer49)
A particular adsorption process has the following characteristics:
|
(i) It arises due to vander Waals forces and
|
|
(ii) it is reversible. Identify the correct statement that describes the above adsorption process:
|
JEE Main Online Paper (Held On 09 April 2016)
A)
Enthalpy of adsorption is greater than \[100 \text{kJ}\,\text{mo}{{\text{l}}^{\text{-1}}}.\]
done
clear
B)
Adsorption is monolayer.
done
clear
C)
Adsorption increases with increase in temperature.
done
clear
D)
Energy of activation is low.
done
clear
View Answer play_arrow
-
question_answer50)
The plot shows the variation of .ln Kp versus temperature for the two reactions.
|
\[M(s)+\frac{1}{2}{{O}_{2}}(g)\xrightarrow[{}]{{}}MO(s)\]and
|
|
\[C(s)+\frac{1}{2}{{O}_{2}}(g)\xrightarrow[{}]{{}}CO(s)\]
|
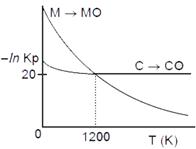 |
Identify the correct statement:
JEE Main Online Paper (Held On 09 April 2016)
A)
At T > 1200 K, carbon will reduce MO(s) to M(s).
done
clear
B)
At T < 1200 K, oxidation of carbon is unfavourable.
done
clear
C)
Oxidation of carbon is favourable at all temperatures.
done
clear
D)
At \[T<1200K,\] the reaction \[MO(s)+C(s)\to M(s)+CO(g)\]is spontaneous.
done
clear
View Answer play_arrow
-
question_answer51) BOD stands for:
JEE Main Online Paper (Held On 09 April 2016)
A)
Biochemical Oxygen Demand
done
clear
B)
Biochemical Oxidation Demand
done
clear
C)
Biological Oxygen Demand
done
clear
D)
Bacterial Oxidation Demand
done
clear
View Answer play_arrow
-
question_answer52) What will occur if a block of copper metal is dropped into a beaker containing a solution of\[1MZnS{{O}_{4}}?\]
JEE Main Online Paper (Held On 09 April 2016)
A)
The copper metal will dissolve and zinc metal will be deposited.
done
clear
B)
The copper metal will dissolve with evolution of oxygen gas.
done
clear
C)
The copper metal will dissolve with evolution of hydrogen gas.
done
clear
D)
No reaction will occur.
done
clear
View Answer play_arrow
-
question_answer53) The test to distinguish primary, secondary and tertiary amine is:
JEE Main Online Paper (Held On 09 April 2016)
A)
Mustard oil test
done
clear
B)
\[{{C}_{6}}{{H}_{5}}S{{O}_{2}}Cl\]
done
clear
C)
Sandmeyer's reaction
done
clear
D)
Carbylamine reaction
done
clear
View Answer play_arrow
-
question_answer54) The total number of orbitals associated with the principal quantum number 5 is:
JEE Main Online Paper (Held On 09 April 2016)
A)
5
done
clear
B)
20
done
clear
C)
25
done
clear
D)
10
done
clear
View Answer play_arrow
-
question_answer55) The correct order of the solubility of alkaline-earth metal sulphates in water is:
JEE Main Online Paper (Held On 09 April 2016)
A)
Mg < Sr < Ca < Ba
done
clear
B)
Mg > Ca> Sr > Ba
done
clear
C)
Mg > Sr > Ca > Ba
done
clear
D)
Mg < Ca < Sr < Ba
done
clear
View Answer play_arrow
-
question_answer56) An organic compound contains C, H and S. The minimum molecular weight of the compound containing 8% sulphur is: (atomic weight of S = 32 amu)
JEE Main Online Paper (Held On 09 April 2016)
A)
300 g \[\text{mo}{{\text{l}}^{\text{-1}}}\]
done
clear
B)
400 g \[\text{mo}{{\text{l}}^{\text{-1}}}\]
done
clear
C)
200 g \[\text{mo}{{\text{l}}^{\text{-1}}}\]
done
clear
D)
600 g \[\text{mo}{{\text{l}}^{\text{-1}}}\]
done
clear
View Answer play_arrow
-
question_answer57) Bouveault-Blanc reduction reaction involves:
JEE Main Online Paper (Held On 09 April 2016)
A)
Reduction of an anhydride with \[LiAl{{H}_{4}}.\]
done
clear
B)
Reduction of an ester with \[Na/{{C}_{2}}{{H}_{5}}OH.\]
done
clear
C)
Reduction of a carbonyl compound with Na/Hg and HCl.
done
clear
D)
Reduction of an acyl halide with H2/Pd.
done
clear
View Answer play_arrow
-
question_answer58)
Consider the following sequence for aspartic acid: 
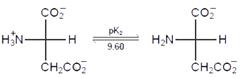 The pl (isoelectric point) of aspartic acid is:
JEE Main Online Paper (Held On 09 April 2016)
The pl (isoelectric point) of aspartic acid is:
JEE Main Online Paper (Held On 09 April 2016)
A)
5.74
done
clear
B)
3.65
done
clear
C)
2.77
done
clear
D)
1.88
done
clear
View Answer play_arrow
-
question_answer59) The amount of arsenic pentasulphide that can be obtained when 35.5 g arsenic acid is treated with excess \[{{H}_{2}}S\]in the presence of conc. HCl (assuming 100% conversion)
JEE Main Online Paper (Held On 09 April 2016)
A)
0.25 mol
done
clear
B)
0.125 mol
done
clear
C)
0.333 mol
done
clear
D)
0.50 mol
done
clear
View Answer play_arrow
-
question_answer60) The solubility of \[{{N}_{2}}\]in water at 300 K and 500 torr partial pressure is 0.01 g \[{{\text{L}}^{\text{-1}}}\]. The solubility (in g \[{{\text{L}}^{\text{-1}}}\]) at 750 torr partial pressure is :
JEE Main Online Paper (Held On 09 April 2016)
A)
0.02
done
clear
B)
0.015
done
clear
C)
0.0075
done
clear
D)
0.005
done
clear
View Answer play_arrow
-
question_answer61) If A and B are any two events such that P(A) =2/5 and \[P(A\cap B)=3/20,\]then the conditional probability, \[P(A/(A'\cap B')),\]where A' denotes the complement of A, is equal to :
A)
\[\frac{8}{17}\]
done
clear
B)
\[\frac{1}{4}\]
done
clear
C)
\[\frac{5}{17}\]
done
clear
D)
\[\frac{11}{20}\]
done
clear
View Answer play_arrow
-
question_answer62) For \[x\in R,x\ne 0,x\ne 1,\]let\[{{f}_{0}}(x)=\frac{1}{1-x}\]and\[{{f}_{n+1}}(x)={{f}_{0}}(f{{(}_{n}}(X)),\]n = 0, 1, 2, ........ Then the value of \[{{f}_{100}}(3)+{{f}_{1}}\left( \frac{2}{3} \right)+{{f}_{2}}\left( \frac{3}{2} \right)\]is equal to:
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{4}{3}\]
done
clear
B)
\[\frac{1}{3}\]
done
clear
C)
\[\frac{5}{3}\]
done
clear
D)
\[\frac{8}{3}\]
done
clear
View Answer play_arrow
-
question_answer63) The distance of the point (1, .2, 4) from the plane passing through the point (1, 2, 2) and perpendicular to the planes \[x-y+2z=3\] and \[2x-2y+z+12=0\], is
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{1}{\sqrt{2}}\]
done
clear
B)
2
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[2\sqrt{2}\]
done
clear
View Answer play_arrow
-
question_answer64) If the equations \[{{x}^{2}}+bx-1=0\]and \[{{x}^{2}}+x+b=0\]have a common root different from . 1, then | b | is equal to
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\sqrt{2}\]
done
clear
B)
2
done
clear
C)
\[\sqrt{3}\]
done
clear
D)
3
done
clear
View Answer play_arrow
-
question_answer65) If \[2\int\limits_{0}^{1}{{{\tan }^{-1}}xdx}=\int\limits_{0}^{1}{{{\cot }^{-1}}}(1-x+{{x}^{2}})dx\]then\[\int\limits_{0}^{1}{{{\tan }^{-1}}}(1-x+{{x}^{2}})dx\]is equal to:
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\log 2\]
done
clear
B)
\[\frac{\pi }{2}+\log 2\]
done
clear
C)
\[\log 4\]
done
clear
D)
\[\frac{\pi }{2}-\log 4\]
done
clear
View Answer play_arrow
-
question_answer66) If \[P=\left[ \begin{matrix} \frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \\ \end{matrix} \right],A=\left[ \begin{matrix} 1 & 1 \\ 0 & 1 \\ \end{matrix} \right]\]and\[Q=PA{{P}^{T}},\]then\[{{P}^{T}}{{Q}^{2015}}P\]is
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\left[ \begin{matrix} 2015 & 1 \\ 0 & 2015 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 1 & 2015 \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 0 & 2015 \\ 0 & 0 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 2015 & 0 \\ 1 & 2015 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
-
question_answer67) If\[\int_{{}}^{{}}{\frac{dx}{{{\cos }^{3}}x\sqrt{2\sin 2x}}={{(\tan x)}^{A}}}+C{{(\tan x)}^{B}}+k,\] where k is a constant of integration, then A + B + C equals
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{16}{5}\]
done
clear
B)
\[\frac{21}{5}\]
done
clear
C)
\[\frac{7}{10}\]
done
clear
D)
\[\frac{27}{10}\]
done
clear
View Answer play_arrow
-
question_answer68) The point (2, 1) is translated parallel to the line \[L:x-y=4\]by \[2\sqrt{3}\]units. If the new point Q lies in the third quadrant, then the equation of the line passing through Q and perpendicular to L is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[2x+2y=1-\sqrt{6}\]
done
clear
B)
\[x=y=3-3\sqrt{6}\]
done
clear
C)
\[x+y=2-\sqrt{6}\]
done
clear
D)
\[x+y=3-2\sqrt{6}\]
done
clear
View Answer play_arrow
-
question_answer69) If the function \[f(x)=\left\{ \begin{matrix} -x, & x<1 \\ a+{{\cos }^{-1}} & (x+b),1\le x\le 2 \\ \end{matrix} \right.\] is differentiable at x = 1, then\[\frac{a}{b}\]is equal to :
A)
\[\frac{-\pi -2}{2}\]
done
clear
B)
\[-1-{{\cos }^{-1}}(2)\]
done
clear
C)
\[\frac{\pi +2}{2}\]
done
clear
D)
\[\frac{\pi -2}{2}\]
done
clear
View Answer play_arrow
-
question_answer70) The value of\[\sum\limits_{r=1}^{15}{{{r}^{2}}}\left( \frac{^{15}{{C}_{r}}}{^{15}{{C}_{r-1}}} \right)\]is equal to
JEE Main Online Paper (Held On 09 April 2016)
A)
1085
done
clear
B)
560
done
clear
C)
680
done
clear
D)
1240
done
clear
View Answer play_arrow
-
question_answer71) In a triangle ABC, right angled at the vertex A, if the position vectors of A, B and C are respectively \[3\hat{i}+\hat{j}-\hat{k},-\hat{i}+3\hat{j}+p\hat{k}\]and\[5\hat{i}+q\hat{j}-4\hat{k},\]then the point (p, q) lies on a line
JEE Main Online Paper (Held On 09 April 2016)
A)
parallel to y-axis
done
clear
B)
making an acute angle with the positive direction of x-axis
done
clear
C)
parallel to x-axis
done
clear
D)
making an obtuse angle with the position direction of x-axis.
done
clear
View Answer play_arrow
-
question_answer72) If\[\underset{x\to \infty }{\mathop{Lim}}\,{{\left( 1+\frac{a}{x}-\frac{4}{{{x}^{2}}} \right)}^{2x}}={{e}^{3}},\]then ?a? is equal to:
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{2}{3}\]
done
clear
B)
\[\frac{3}{2}\]
done
clear
C)
2
done
clear
D)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
-
question_answer73) The number of \[x\in [0,2\pi ]\]for which\[\left| \sqrt{2{{\sin }^{4}}x+18{{\cos }^{2}}x}-\sqrt{2{{\cos }^{4}}x+18{{\sin }^{2}}x} \right|=1\]
JEE Main Online Paper (Held On 09 April 2016)
A)
6
done
clear
B)
4
done
clear
C)
8
done
clear
D)
2
done
clear
View Answer play_arrow
-
question_answer74) If m and M are the minimum and the maximum values of \[4+\frac{1}{2}{{\sin }^{2}}2x-2{{\cos }^{4}}x,x\in R,\]then M-m is equal to
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{7}{4}\]
done
clear
B)
\[\frac{15}{4}\]
done
clear
C)
\[\frac{9}{4}\]
done
clear
D)
\[\frac{1}{4}\]
done
clear
View Answer play_arrow
-
question_answer75) If a variable line drawn through the intersection of the lines\[\frac{x}{3}+\frac{y}{4}=1\]and\[\frac{x}{4}+\frac{y}{3}=1,\] meets the coordinate axes at A and B, \[(A\ne B),\] then the locus of the midpoint of AB is
JEE Main Online Paper (Held On 09 April 2016)
A)
\[7xy=6(x+y)\]
done
clear
B)
\[6xy=7(x+y)\]
done
clear
C)
\[4{{(x+y)}^{2}}-28(x+y)+49=0\]
done
clear
D)
\[14{{(x+y)}^{2}}-97(x+y)+168=0\]
done
clear
View Answer play_arrow
-
question_answer76) If f(x) is a differentiable function in the interval \[(0,\,\,\infty )\] such that f(1) = 1 and \[\underset{t\to x}{\mathop{Lim}}\,\frac{{{t}^{2}}f(x)-{{x}^{2}}f(t)}{t-x}=1,\]for each x > 0, then \[f\left( \frac{3}{2} \right)\] is equal to :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{13}{6}\]
done
clear
B)
\[\frac{23}{18}\]
done
clear
C)
\[\frac{25}{9}\]
done
clear
D)
\[\frac{31}{18}\]
done
clear
View Answer play_arrow
-
question_answer77) If the tangent at a point P, with parameter t, on the curve \[x=4{{t}^{2}}+3,y=8{{t}^{3}}-1,t\in R,\]meets the curve again at a point Q, then the coordinates of Q are :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[({{t}^{2}}+3,-{{t}^{3}}-1)\]
done
clear
B)
\[({{t}^{2}}+3,{{t}^{3}}-1)\]
done
clear
C)
\[(16{{t}^{2}}+3,-64{{t}^{3}}-1)\]
done
clear
D)
\[(4{{t}^{2}}+3,-4{{t}^{3}}-1)\]
done
clear
View Answer play_arrow
-
question_answer78) If the tangent at a point on the ellipse\[\frac{{{x}^{2}}}{27}+\frac{{{y}^{2}}}{3}=1\]meets the coordinate axes at A and B, and O is the origin, then the minimum area (in sq. units) of the triangle OAB is :
JEE Main Online Paper (Held On 09 April 2016)
A)
9
done
clear
B)
\[\frac{9}{2}\]
done
clear
C)
\[9\sqrt{3}\]
done
clear
D)
\[3\sqrt{3}\]
done
clear
View Answer play_arrow
-
question_answer79) The point represented by 2+i in the Arg and plane moves 1 unit eastwards, then 2 units northwards and finally from there 2 2 units in the south-westwards direction. Then its new position in the Argand plane is at the point represented by :
JEE Main Online Paper (Held On 09 April 2016)
A)
2 + 2i
done
clear
B)
- 2 - 2i
done
clear
C)
1 + i
done
clear
D)
- 1 - i
done
clear
View Answer play_arrow
-
question_answer80) A circle passes through (-2, 4). Which one of the following equations can represent a diameter of this circle?
JEE Main Online Paper (Held On 09 April 2016)
A)
\[4x+5y-6=0\]
done
clear
B)
\[5x+2y+4=0\]
done
clear
C)
\[2x-3y+10=0\]
done
clear
D)
\[3x+4y-3=0\]
done
clear
View Answer play_arrow
-
question_answer81) The number of distinct real roots of the equation,\[\left| \begin{matrix} \cos x & \sin x & \sin x \\ \sin x & \cos x & \sin x \\ \sin x & \sin x & \cos x \\ \end{matrix} \right|=0\]in the interval \[\left[ -\frac{\pi }{4},\frac{\pi }{4} \right]\]is:
JEE Main Online Paper (Held On 09 April 2016)
A)
4
done
clear
B)
1
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
-
question_answer82) The shortest distance between the lines\[\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\]and\[\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\]lies in the interval :
JEE Main Online Paper (Held On 09 April 2016)
A)
(2, 3]
done
clear
B)
[0, 1)
done
clear
C)
(3, 4]
done
clear
D)
[1, 2)
done
clear
View Answer play_arrow
-
question_answer83) If the four letter words (need not be meaningful) are to be formed using the letters from the word MEDITERRANEAN. such that the first letter is R and the fourth letter is E, then the total number of all such words is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{11!}{{{(2!)}^{3}}}\]
done
clear
B)
59
done
clear
C)
110
done
clear
D)
56
done
clear
View Answer play_arrow
-
question_answer84) Let a and b respectively be the semi-transverse and semi-conjugate axes of a hyperbola whose eccentricity satisfies the equation \[\text{9e}{{\text{-}}^{\text{2}}}\text{-18e}+\text{5}=0.\] If S(5, 0) is a focus and 5x = 9 is the corresponding directrix of hyperbola, then \[{{a}^{2}}-{{b}^{2}}\]is equal to
JEE Main Online Paper (Held On 09 April 2016)
A)
- 7
done
clear
B)
- 5
done
clear
C)
5
done
clear
D)
7
done
clear
View Answer play_arrow
-
question_answer85) Consider the following two statements : P : If 7 is an odd number, then 7 is divisible by 2. Q : If 7 is a prime number, then 7 is an odd number. If \[{{V}_{1}}\]is the truth value of contrapositive of P and \[{{V}_{2}}\] is the truth value of contrapositive of Q, then the ordered pair \[({{V}_{1}},{{V}_{2}})\] equals :
JEE Main Online Paper (Held On 09 April 2016)
A)
(F, T)
done
clear
B)
(T, F)
done
clear
C)
(F, F)
done
clear
D)
(T, T)
done
clear
View Answer play_arrow
-
question_answer86) The minimum distance of a point on the curve \[y={{x}^{2}}-4\] from the origin is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{\sqrt{15}}{2}\]
done
clear
B)
\[\frac{\sqrt{19}}{2}\]
done
clear
C)
\[\sqrt{\frac{15}{2}}\]
done
clear
D)
\[\sqrt{\frac{19}{2}}\]
done
clear
View Answer play_arrow
-
question_answer87) Let x, y, z be positive real numbers such that \[\text{x}+\text{y}+\text{z}=\text{12}\]and \[{{x}^{3}}{{y}^{4}}{{z}^{5}}=(0.1){{(600)}^{3}}.\]Then \[{{x}^{3}}+{{y}^{3}}+{{z}^{3}}\] is equal to
JEE Main Online Paper (Held On 09 April 2016)
A)
270
done
clear
B)
258
done
clear
C)
216
done
clear
D)
342
done
clear
View Answer play_arrow
-
question_answer88) If the mean deviation of the numbers 1, 1 + d, ..., 1 + 100d from their mean is 255, then a value of d is :
JEE Main Online Paper (Held On 09 April 2016)
A)
10
done
clear
B)
20.2
done
clear
C)
5.05
done
clear
D)
10.1
done
clear
View Answer play_arrow
-
question_answer89) For\[x\in R,x=-1,\]if \[{{(1+x)}^{2016}}+x{{(1+x)}^{2015}}+{{x}^{2}}\]\[{{(1+x)}^{2014}}+...........+{{x}^{2016}}=\]\[\sum\limits_{i=0}^{2016}{{{a}_{i}}{{x}^{i}},}\]then\[{{a}_{17}}\]is equal to:
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{2016!}{16!}\]
done
clear
B)
\[\frac{2017!}{2000!}\]
done
clear
C)
\[\frac{2017!}{17!2000!}\]
done
clear
D)
\[\frac{2016!}{17!1999!}\]
done
clear
View Answer play_arrow
-
question_answer90) The area (in sq. units) of the region described by \[A=\{(x,y)|y\ge {{x}^{2}}-5x+4,x+y\ge 1,y\le 0\}\]is :
JEE Main Online Paper (Held On 09 April 2016)
A)
\[\frac{7}{2}\]
done
clear
B)
\[\frac{13}{6}\]
done
clear
C)
\[\frac{17}{6}\]
done
clear
D)
\[\frac{19}{6}\]
done
clear
View Answer play_arrow
 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)




 Focal length| |Focal length| = 30 cm =120 cm
Focal length| |Focal length| = 30 cm =120 cm  JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)
 JEE Main Online Paper (Held On 09 April 2016)
JEE Main Online Paper (Held On 09 April 2016)


 The pl (isoelectric point) of aspartic acid is:
JEE Main Online Paper (Held On 09 April 2016)
The pl (isoelectric point) of aspartic acid is:
JEE Main Online Paper (Held On 09 April 2016)
