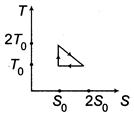
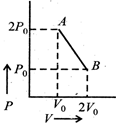
| A system goes from A to B via two processes and II as shown in figure. If |
 |
| When a system is taken from state\[E={{E}_{0}}\]to state f along the path iaf, it is found that\[sin\text{ }\omega t\] and\[I={{I}_{0}}\sin \left( \omega t-\frac{\pi }{2} \right)\]. Along the path ibf, \[p=\frac{{{E}_{0}}{{I}_{0}}}{\sqrt{2}}\]cal. W along the path ibf is [AIEEE 2007] |
 |
| Directions: Question numbers 14 - 16 are based on the following paragraph. |
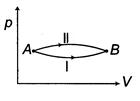
| Two moles of helium gas are taken over the cycle ABCDA, as shown in the P-T diagram. |
 |
| Assuming the gas to be ideal the work done on the gas in taking it from A to B is: [AIEEE 2009] |
| The specific heat capacity of a metal at low temperature (T) is given as : |
| \[{{C}_{p}}(kj{{K}^{-1}}k{{g}^{-1}})=32{{\left( \frac{T}{400} \right)}^{3}}\] |
| A 100 gram vessel of this metal is to be cooled from 20°K to 4°K by a special refrigerator operating at room temperature (27°C). The amount of work required to cool the vessel is: [AIEEE 11-05-2011] |
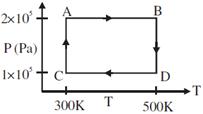
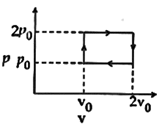
| Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure. Efficiency of this cycle is nearly: [AIEEE 2012] |
| (Assume the gas to be close to ideal gas) |
 |
| This question has Statement 1 and Statement 2. [JEE ONLINE 07-05-2012] |
| Of the four choices given after the Statements, choose the one that best describes the two Statements. |
| Statement 1: In an adiabatic process, change in internal energy of a gas is equal to work done on/ by the gas in the process. |
| Statement 2: The temperature of a gas remains constant in an adiabatic process. |
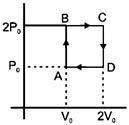
| n moles of an ideal gas undergo a process \[A\to B\]as shown in the figure. Maximum temperature of the gas during the process is [JEE ONLINE 12-05-2012] |
 |
| This question has Statement 1 and Statement 2. |
| Of the four choices given after the Statements, choose the one that best describes the two Statements. |
| Statement 1: An inventor claims to have constructed an engine that has an efficiency of 30% when operated between the boiling and freezing points of water. This is not possible. |
| Statement 2: The efficiency of a real engine is always less than the efficiency of a Carnot engine operating between the same two temperatures. [JEE ONLINE 19-05-2012] |
| The above \[p-v\] diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat, extracted from the source in a single cycle is: [JEE MAIN 2013] |
 |
| Figure shows the variation in temperature \[(\Delta T)\]with the amount of heat supplied \[(Q)\] in an isobaric process corresponding to a monatomic (M), diatomic and a polyatomic (P) gas. The initial state of all the gases are the same and the scales for the two axes coincide, ignoring vibration degrees of freedom, the lines a, b and c respectively correspond to: [JEE ONLINE 09-04-2013] |
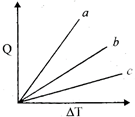 |
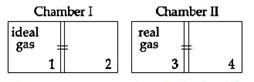 |
| There are two identical chambers, completely thermally insulated from surroundings. Both chambers have a partition wall dividing the chambers in two compartments. Compartment 1 is filled with an ideal gas and compartment 3 id filled with a real gas. Compartments 2 and 4 are vacuum. A small hole (orifice) is made in the partition walls and the gases are allowed to expand in vacuum. |
| Statement-1: No change in the temperature of the gas takes place when ideal as expands in vacuum. However, the temperature of real gas goes down (cooling) when it expands it expands in vacuum. |
| Statement-2: The internal energy of an ideal gas is only kinetic. The internal energy of a real gas is kinetic as well as potential. [JEE ONLINE 09-04-2013] |
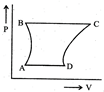
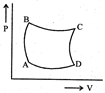
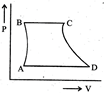
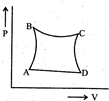
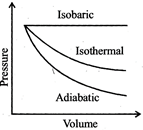
| A sample of gas expands from \[{{\operatorname{V}}_{1}}\] to \[{{\operatorname{V}}_{2}}\]. In which of the following, the work dine will be greatest? |
| [JEE ONLINE 25-04-2013] |
 |
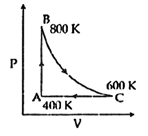
| One mole of diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperatures at A, B and C are 400 K, 800 K and 600 K respectively. Choose the correct statement: [JEE MAIN 2014] |
 |
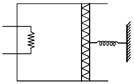
| An ideal monoatomic gas is confined in a cylinder by a spring loaded piston of cross section \[8.0\times {{10}^{-3}}{{m}^{2}}.\] Initially the gas is at 300 K and occupies a volume of \[2.4\times {{10}^{-3}}{{m}^{3}}\] and the spring is in its relaxed state as shown in figure. The gas is heated by a small heater until the piston moves out slowly by 0.1 m. The force constant of the spring is 8000 N/m and the atmospheric pressure is \[1.0\times {{10}^{5}}N/{{m}^{2}}.\] The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. The final temperature of the gas will be: |
| (Neglect the heat loss through the lead wires of the heater. The heat capacity of the heater coil is also negligible). |
| [JEE ONLINE 11-04-2014] |
 |
| A solid body of constant heat capacity 1J/°C is being heated by keeping it in contact with reservoirs in two ways: |
| (i) Sequentially keeping in contact with 2 reservoirs such that each reservoir supplies same amount of heat. |
| (ii) Sequentially keeping in contact with 8 reservoirs such that each reservoir supplies same amount of heat. |
| In both the cases body is brought from initial temperature 100°C to final temperature 200°C. Entropy change of the body in the two cases respectively is: [JEE MAIN 2015] |
| An ideal gas goes through a reversible cycle \[a\to b\to c\to d\]has the V - T diagram shown below. Process \[d\to a\]and \[b\to c\] are adiabatic. [JEE ONLINE 10-04-2015] |
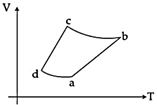 |
| The corresponding P - V diagram for the process is (all figures are schematic and not drawn to scale): |
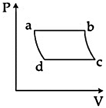
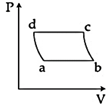
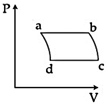
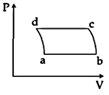
| 'n' moles of an ideal gas undergoes a process \[A\to B\]as shown in the figure. The maximum temperature of the gas during the process will be: [JEE MAIN - I 3-4-2016] |
 |
|
done
clear
C)
0.32
done
clear
D)
0.08
done
clear
View Answer play_arrow
question_answer52) N moles of a diaotmic gas in a cylinder are at a temperature T. Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas get converted into monoatomic gas. What is the change in the total kinetic energy of the gas? [JEE Online 09-04-2017]
A)
0
done
clear
B)
\[\frac{5}{2}nRT\]
done
clear
C)
\[\frac{3}{2}\,nRT\]
done
clear
D)
\[\frac{1}{2}\,nRT\]
done
clear
View Answer play_arrow
question_answer53) Two moles of an ideal monoatomic gas occupies a volume \[V\] at \[27{}^\circ C\]. The gas expands adiabatically to a volume\[\text{2 V}\]. Calculate the final temperature of the gas and change in its internal energy. [JEE Main Online 08-04-2018]
A)
\[\text{(A) 189 K}\text{(B) -2}\text{.7 kj}\]
done
clear
B)
\[\text{(A) 195 K}\text{(B) 2}\text{.7 kj}\]
done
clear
C)
\[\text{(A) 189 K}\text{(B) 2}\text{.7 kj}\]
done
clear
D)
\[\text{(A) 195 K}\text{(B) -2}\text{.7 kj}\]
done
clear
View Answer play_arrow
question_answer54) A Carnot's engine works as a refrigerator between \[250K\] and \[300K\]. It receives \[500cal\] heat from the reservoir at the lower temperature. The amount of work done in each cycle to operate the refrigerator is: [JEE Online 15-04-2018]
A)
\[420J\]
done
clear
B)
\[2100J\]
done
clear
C)
\[772J\]
done
clear
D)
\[2520J\]
done
clear
View Answer play_arrow
question_answer55) One mode of an ideal monoatomic gas is compressed isothermally in a rigid vessel to double its pressure at room temperature, \[27{}^\circ C\]. The work done on the gas will be: [JEE Online 15-04-2018]
A)
\[300R\,\,In\,\,6\]
done
clear
B)
\[300R\]
done
clear
C)
\[300R\,\,In\,\,7\]
done
clear
D)
\[300R\,\,In\,\,2\]
done
clear
View Answer play_arrow
question_answer56) Two Carnot engines A and B are operated in series. Engine A receives heat from a reservoir at \[600K\] and rejects heat to a reservoir heat to reservoir at temperature\[T\]. Engine\[B\] receives heat rejected by engine \[A\] and in turn rejects it to a reservoir at\[100K\]. If the efficiencies of the two engines A and B are represented by \[{{\eta }_{A}}\] and \[{{\eta }_{B}}\] respectively, then what is the value of \[\frac{{{\eta }_{A}}}{{{\eta }_{B}}}\] [JEE Online 15-04-2018 (II)]
A)
\[\frac{12}{7}\]
done
clear
B)
\[\frac{12}{5}\]
done
clear
C)
\[\frac{5}{12}\]
done
clear
D)
\[\frac{7}{12}\]
done
clear
View Answer play_arrow
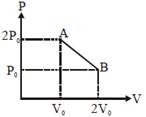
question_answer57)
A)
\[\frac{25}{8}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
B)
\[\frac{25}{4}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
C)
\[\frac{25}{16}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
D)
\[\frac{5}{8}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
View Answer play_arrow
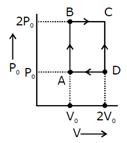
question_answer58)
A)
40 J
done
clear
B)
20 J
done
clear
C)
100 J
done
clear
D)
80 J
done
clear
View Answer play_arrow
question_answer59) Two Carnot engines A and B are operated in series. The first one, A, receives heat at \[{{T}_{1}}\left( =600\text{ }K \right)\] and rejects to a reservoir at temperature Ta. The second engine B receives heat rejected by the first engine and, in turn, rejects to a heat reservoir at\[{{T}_{3}}(=400\text{ }K)\]. Calculate the temperature \[{{T}_{2}}\] if the work outputs of the engines are equal: [JEE Main 09-Jan-2019 Evening]
A)
500 K
done
clear
B)
300 K
done
clear
C)
600 K
done
clear
D)
400 K
done
clear
View Answer play_arrow
question_answer60) Three Carnot engines operate in series between a heat source at a temperature \[{{T}_{1}}\] and a heat sink at temperature \[{{T}_{4}}\] (see figure). There are two other reservoirs at temperature\[{{T}_{2}}and\text{ }{{T}_{3}}\], as shown, with\[{{T}_{1}}>{{T}_{2}}>{{T}_{3}}>{{T}_{4}}\]. The three engines are equally efficient if - [JEE Main 10-Jan-2019 Morning]
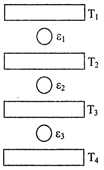
A)
\[{{T}_{2}}=\,\,{{({{T}_{1}}^{3}{{T}_{4}})}^{1/4}};\,\,=\,\,{{T}_{3}}\,\,=\,\,{{({{T}_{1}}{{T}_{4}}^{3})}^{1/4}}\]
done
clear
B)
\[{{T}_{2}}=\,\,{{({{T}_{1}}{{T}_{4}})}^{1/2}};\,\,\,{{T}_{3}}\,\,=\,\,{{({{T}_{1}}^{2}{{T}_{4}})}^{1/3}}\]
done
clear
C)
\[{{T}_{2}}=\,\,{{({{T}_{1}}{{T}_{4}}^{2})}^{1/3}};\,\,{{T}_{3}}\,\,=\,\,{{({{T}_{1}}^{2}{{T}_{4}})}^{1/3}}\]
done
clear
D)
\[{{T}_{2}}=\,\,{{({{T}_{1}}^{2}{{T}_{4}})}^{1/3}};\,\,\,\,{{T}_{3}}\,\,=\,\,{{({{T}_{1}}{{T}_{4}}^{2})}^{1/3}}\]
done
clear
View Answer play_arrow
question_answer61) Half mole of an ideal monoatomic gas is heated at constant pressure of 1 atm from\[20{}^\circ C\text{ }to\text{ }90{}^\circ C\]. Work done by gas is close to - (Gas constant \[R=8.31\text{ }J\] /mol. K) [JEE Main 10-Jan-2019 Evening]
A)
581 J
done
clear
B)
73 J
done
clear
C)
146 J
done
clear
D)
291 J
done
clear
View Answer play_arrow
question_answer62) A rigid diatomic ideal gas undergoes an adiabatic process at room temperature. The relation between temperature and volume for this process is \[T{{V}^{x}}=\]constant, then x is- [JEE Main 11-Jan-2019 Morning]
A)
\[\frac{2}{3}\]
done
clear
B)
\[\frac{3}{5}\]
done
clear
C)
\[\frac{2}{5}\]
done
clear
D)
\[\frac{5}{3}\]
done
clear
View Answer play_arrow
question_answer63) A gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T. Considering only translational and rotational modes, the total internal energy of the system is- [JEE Main 11-Jan-2019 Morning]
A)
20 RT
done
clear
B)
12 RT
done
clear
C)
4 RT
done
clear
D)
15 RT
done
clear
View Answer play_arrow
question_answer64)
A)
10 J
done
clear
B)
1 J
done
clear
C)
5 J
done
clear
D)
30 J
done
clear
View Answer play_arrow
question_answer65) A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is\[{{l}_{1}}\]and that below the piston is\[{{l}_{2}},\]such that \[{{l}_{1}}>{{l}_{2}}.\]Each part of the cylinder contains n moles of an ideal gas at equal temperature T. If the piston is stationary, its mass m, will be given by (R is universal gas constant and g is the acceleration due to gravity) [JEE Main 12-Jan-2019 Evening]
A)
\[\frac{RT}{ng}\left[ \frac{{{l}_{1}}-3{{l}_{2}}}{{{l}_{1}}{{l}_{2}}} \right]\]
done
clear
B)
\[\frac{nRT}{g}\left[ \frac{1}{{{l}_{2}}}+\frac{1}{{{l}_{1}}} \right]\]
done
clear
C)
\[\frac{RT}{g}\left[ \frac{2{{l}_{1}}+{{l}_{2}}}{{{l}_{1}}{{l}_{2}}} \right]\]
done
clear
D)
\[\frac{nRT}{g}\left[ \frac{{{l}_{1}}-{{l}_{2}}}{{{l}_{1}}{{l}_{2}}} \right]\]
done
clear
View Answer play_arrow
question_answer66)
A)
\[8.85\times {{10}^{-10}}C\]
done
clear
B)
\[7.85\times {{10}^{-10}}C\]
done
clear
C)
\[9.85\times {{10}^{-10}}C\]
done
clear
D)
\[6.85\times {{10}^{-10}}C\]
done
clear
View Answer play_arrow
question_answer67) A thermally insulated vessel contains 150g of water at \[0{}^\circ C\]. Then the air from the vessel is pumped out adiabatically. A fraction of water turns into ice and the rest evaporates at \[0{}^\circ C\] itself. The mass of evaporated water will be closest to: (Latent heat of vaporization of water \[=2.10\times {{10}^{6}}Jk{{g}^{1}}\] and Latent heat of Fusion of water \[=3.36\times {{10}^{5}}Jk{{g}^{1}}\]) [JEE Main 8-4-2019 Morning]
A)
130 g
done
clear
B)
35 g
done
clear
C)
20 g
done
clear
D)
150 g
done
clear
View Answer play_arrow
question_answer68)
A)
d a c b
done
clear
B)
a d c b
done
clear
C)
a d b c
done
clear
D)
d a b c
done
clear
View Answer play_arrow
question_answer69)
A)
\[\Delta {{Q}_{A}}=\Delta {{Q}_{B}};\Delta {{U}_{A}}=\Delta {{U}_{B}}\]
done
clear
B)
\[\Delta {{Q}_{A}}>\Delta {{Q}_{B}};\Delta {{U}_{A}}=\Delta {{U}_{B}}\]
done
clear
C)
\[\Delta {{Q}_{A}}>\Delta {{Q}_{B}};\Delta {{U}_{A}}>\Delta {{U}_{B}}\]
done
clear
D)
\[\Delta {{Q}_{A}}<\Delta {{Q}_{B}};\Delta {{U}_{A}}<\Delta {{U}_{B}}\]
done
clear
View Answer play_arrow
question_answer70) n moles of an ideal gas with constant volume heat capcity \[{{C}_{V}}\]undergo an isobaric expansion by certain volume. The ratio of the work done in the process, to the heat supplied is: [JEE Main 10-4-2019 Morning]
A)
\[\frac{4nR}{{{C}_{V}}-nR}\]
done
clear
B)
\[\frac{nR}{{{C}_{V}}-nR}\]
done
clear
C)
\[\frac{nR}{{{C}_{V}}+nR}\]
done
clear
D)
\[\frac{4nR}{{{C}_{V}}+nR}\]
done
clear
View Answer play_arrow
question_answer71) When heat Q is supplied to a diatomic gas of rigid molecules, at constant volume its temperature increases by \[\Delta T.\]The heat required to produce the same change in temperature, at a constant pressure is : [JEE Main 10-4-2019 Afternoon]
A)
\[\frac{7}{5}Q\]
done
clear
B)
\[\frac{3}{2}Q\]
done
clear
C)
\[\frac{5}{3}Q\]
done
clear
D)
\[\frac{2}{3}Q\]
done
clear
View Answer play_arrow
question_answer72) One mole of an ideal gas passes through a process where pressure and volume obey the relation \[P={{P}_{0}}\left[ 1-\frac{1}{2}{{\left( \frac{{{V}_{0}}}{V} \right)}^{2}} \right].\] Here \[{{P}_{0}}\]and \[{{V}_{0}}\] are constants. Calculate the change in the temperature of the gas if its volume changes from \[{{V}_{0}}\] to \[2{{V}_{0}}\]. [JEE Main 10-4-2019 Afternoon]
A)
\[\frac{1}{2}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
B)
\[\frac{3}{4}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
C)
\[\frac{5}{4}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
D)
\[\frac{1}{4}\frac{{{P}_{0}}{{V}_{0}}}{R}\]
done
clear
View Answer play_arrow
question_answer73)
A)
100 J
done
clear
B)
120 J
done
clear
C)
140 J
done
clear
D)
130 J
done
clear
View Answer play_arrow
question_answer74) A Carnot engine has an efficiency of 1/6. When the temperature of the sink is reduced by \[62{}^\text{o}C\], its efficiency is doubled. The temperatures of the source and the sink are, respectively [JEE Main 12-4-2019 Afternoon]
A)
\[124{}^\text{o}C,62{}^\text{o}C\]
done
clear
B)
\[37{}^\text{o}C,99{}^\text{o}C\]
done
clear
C)
\[62{}^\text{o}C,124{}^\text{o}C\]
done
clear
D)
\[99{}^\text{o}C,37{}^\text{o}C\]
done
clear
View Answer play_arrow
question_answer75) A diatomic gas with rigid molecules does 10 J of work when expanded at constant pressure. What would be the heat energy absorbed by the gas, in this process? [JEE Main 12-4-2019 Afternoon]
A)
35 J
done
clear
B)
40 J
done
clear
C)
25 J
done
clear
D)
30 J
done
clear
View Answer play_arrow
question_answer76) A litre of dry air at STP expands adiabatically to a volume of 3 litres. If \[\gamma =1.40\], the work done by air is \[\left( {{3}^{1.4}}=4.6555 \right)\] [Take air to be an ideal gas] [JEE MAIN Held on 07-01-2020 Morning]
A)
90.5 J
done
clear
B)
60.7 J
done
clear
C)
48 J
done
clear
D)
100.8 J
done
clear
View Answer play_arrow
question_answer77) A Carnot engine operates between two reservoirs of temperatures 900 K and 300 K. The engine performs 1200 J of work per cycle. The heat energy (in J) delivered by the engine to the low temperature reservoir, in a cycle, is_______. [JEE MAIN Held on 07-01-2020 Morning]
View Answer play_arrow
question_answer78) Two ideal Carnot engines operate in cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures, \[{{T}_{1}}\]and \[{{T}_{2}}\]. The temperature of the hot reservoir of the first engine is \[{{T}_{1}}\] and the temperature of the cold reservoir of the second engine is\[{{T}_{2}}\]. \[T\] is temperature of the sink of first engine which is also the source for the second engine. How is \[T\] related to \[{{T}_{1}}\] and\[{{T}_{2}}\], if both the engines perform equal amount of work? [JEE MAIN Held on 07-01-2020 Evening]
A)
\[T=\frac{{{T}_{1}}+{{T}_{2}}}{2}\]
done
clear
B)
\[T=\sqrt{{{T}_{1}}{{T}_{2}}}\]
done
clear
C)
\[T=\frac{2{{T}_{1}}{{T}_{2}}}{{{T}_{1}}+{{T}_{2}}}\]
done
clear
D)
\[T=0\]
done
clear
View Answer play_arrow
question_answer79) Under an adiabatic process, the volume of an ideal gas gets doubled. Consequently the mean collision time between the gas molecule changes from \[{{\tau }_{1}}\] to\[{{\tau }_{2}}\]. If \[\frac{{{C}_{P}}}{{{C}_{v}}}=\gamma \]for this gas then a good estimate for \[\frac{{{\tau }_{2}}}{{{\tau }_{1}}}\]is given by [JEE MAIN Held on 07-01-2020 Evening]
A)
\[{{\left( \frac{1}{2} \right)}^{\frac{\gamma +1}{2}}}\]
done
clear
B)
\[{{\left( \frac{1}{2} \right)}^{\gamma }}\]
done
clear
C)
\[2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
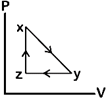
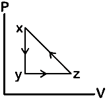
question_answer80)
A)
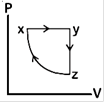
B)
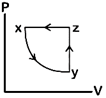
C)
D)
question_answer81) A Carnot engine having an efficiency of \[\frac{1}{10}\] is being used as a refrigerator. If the work done on the refrigerator is 10 J, the amount of heat absorbed from the reservoir at lower temperature is : [JEE MAIN Held on 08-01-2020 Evening]
A)
90 J
done
clear
B)
1 J
done
clear
C)
99 J
done
clear
D)
100 J
done
clear
View Answer play_arrow
question_answer82)
A)
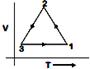
B)
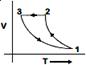
C)
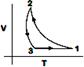
D)
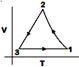
question_answer83) Starting at temperature \[300\text{ }K,\]one mole of an ideal diatomic gas \[(\gamma =1.4)\] is first compressed adiabatically from volume \[{{V}_{1}}\] to \[{{V}_{2}}=\frac{{{V}_{1}}}{16}.\]It is then allowed to expand isobarically to volume \[2{{V}_{2}}\]. If all the processes are the quasi-static then the final temperature of the gas (in \[{}^\circ K\]) is (to the nearest integer) _______. [JEE MAIN Held on 09-01-2020 Evening]
View Answer play_arrow
Study Package
You need to login to perform this action. |