Solved papers for RAJASTHAN ­ PET Rajasthan PET Solved Paper-2009

done Rajasthan PET Solved Paper-2009 Total Questions - 120

• question_answer1) Which of the following equation represents a progressive wave?
  A)
   \[y=\,A\cos \,ax\,\sin bt\]
  done clear
  B)
   \[y=\,A\,\sin \,bt\]
  done clear
  C)
   \[y=\,A\,\cos (ax+bt)\]  
  done clear
  D)
   \[y=\,A\,\tan (ax+bt)\]
  done clear
  View Answer play_arrow

• question_answer2) The frequency and velocity of sound wave are 600 Hz and 360 m/s respectively. Phase difference between two particles of medium are\[60{}^\circ ,\]the minimum distance between these two particles will be
  A)
   10 cm           
  done clear
  B)
   15 cm
  done clear
  C)
   20 cm           
  done clear
  D)
   50 cm
  done clear
  View Answer play_arrow

• question_answer3) The heat required to increase the temperature of 4 moles of a monoatomic ideal gas from 273 K to 473 K at constant volume is
  A)
   200 H            
  done clear
  B)
   400 R
  done clear
  C)
   800 J           
  done clear
  D)
   1200 R
  done clear
  View Answer play_arrow

• question_answer4) A solid sphere rolls without slipping on the roof. The ratio of its rotational kinetic energy and its total kinetic energy is
  A)
   2/5
  done clear
  B)
   4/5
  done clear
  C)
   2/7    
  done clear
  D)
   3/7
  done clear
  View Answer play_arrow

• question_answer5) A black body at a temperature of 2600 K has the wavelength corresponding to maximum emission 1200\[\overset{o}{\mathop{\text{A}}}\,\]. Assuming the moon to be perfectly black body the temperature of the moon, if the wavelength corresponding to maximum emission is 5000\[\overset{o}{\mathop{\text{A}}}\,\] is
  A)
   7800 K          
  done clear
  B)
   6240 K
  done clear
  C)
   5240 K          
  done clear
  D)
   3640 K
  done clear
  View Answer play_arrow

• question_answer6) When the light enters from air to glass, for which colour the angle of deviation is maximum?
  A)
   Red              
  done clear
  B)
   Yellow
  done clear
  C)
   Blue              
  done clear
  D)
   Violet
  done clear
  View Answer play_arrow

• question_answer7) Two waves are represent by \[{{y}_{1}}=A\sin (kx-\omega t)\,and\,{{y}_{2}}=A\cos \,(kx-\omega t)\] The amplitude of resultant wave is
  A)
   4A               
  done clear
  B)
   2A
  done clear
  C)
   \[\sqrt{2}A\]             
  done clear
  D)
   A
  done clear
  View Answer play_arrow

• question_answer8) Which of the following event, support the quantum nature of light?
  A)
   Diffraction
  done clear
  B)
   Polarization
  done clear
  C)
   Interference
  done clear
  D)
   Photoelectric effect
  done clear
  View Answer play_arrow

• question_answer9) The linear momentum of photon is p. The wavelength of photon is \[\lambda \], then (\[h\]is Planck?s constant)
  A)
   \[\lambda =hp\]
  done clear
  B)
   \[\lambda =\frac{h}{p}\]
  done clear
  C)
   \[\lambda =\frac{p}{h}\]
  done clear
  D)
   \[\lambda =\frac{{{p}^{2}}}{h}\]
  done clear
  View Answer play_arrow

• question_answer10) When two coherent monochromatic beams of intensity I and 9l interfere, the possible maximum and minimum intensities of the resulting beam are
  A)
   \[9I\] and\[I\]         
  done clear
  B)
   \[9I\]and\[4I\]
  done clear
  C)
   \[16I\]and\[4I\]       
  done clear
  D)
   \[16I\]and\[I\]
  done clear
  View Answer play_arrow

• question_answer11) An atom of mass M which is in the state of rest emits a photon of wavelength \[\lambda \] . As a result, the atom will deflect with the kinetic energy equal to (A is Planck's constant)
  A)
   \[\frac{{{h}^{2}}}{M{{\lambda }^{2}}}\]
  done clear
  B)
   \[\frac{1}{2}\frac{{{h}^{2}}}{M{{\lambda }^{2}}}\]
  done clear
  C)
   \[\frac{h}{M\lambda }\]
  done clear
  D)
   \[\frac{1}{2}\frac{h}{M\lambda }\]   
  done clear
  View Answer play_arrow

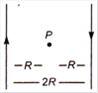
• question_answer12) Two long straight wires are set parallel to each other Each carries a current i in the opposite direction and the separation between them is 2R. The intensity of the magnetic field midway between them is
  A)
   zero              
  done clear
  B)
   \[\frac{{{\mu }_{0}}i}{4\pi R}\]
  done clear
  C)
   \[\frac{{{\mu }_{0}}i}{2\pi R}\]             
  done clear
  D)
   \[\frac{{{\mu }_{0}}i}{\pi R}\]
  done clear
  View Answer play_arrow

• question_answer13) Charge Q is placed at the diagonal faced comers of a square and charge q is placed at another two corners of square. The condition for net electric force on Q to be zero will be
  A)
   \[Q=(-2\sqrt{2)}\,q\]
  done clear
  B)
   \[Q=-\frac{q}{2}\]
  done clear
  C)
   \[Q=(2\sqrt{2)}\,q\]       
  done clear
  D)
   \[Q=-\frac{q}{2}\]
  done clear
  View Answer play_arrow

• question_answer14) The electric potential at centre of metallic conducting sphere is
  A)
   zero
  done clear
  B)
   half from potential at surface of sphere
  done clear
  C)
   equal from potential at surface of sphere
  done clear
  D)
   twice from potential at surface of sphere
  done clear
  View Answer play_arrow

• question_answer15) A capacitor of capacity 10 \[\mu \]F is charged to a potential of 400 Volt. When its both plates are connected by a conducting wire, then heat generated will be
  A)
   \[80\text{ }J\]             
  done clear
  B)
   \[0.8\text{ }J\]
  done clear
  C)
   \[8\times {{10}^{-3}}\]         
  done clear
  D)
    \[8\times {{10}^{-6}}J\]
  done clear
  View Answer play_arrow

• question_answer16) Magnet moment of bar magnet is M. The work done to turn the magnet by\[90{}^\circ \]of magnet in direction of magnetic field B will be
  A)
   zero             
  done clear
  B)
  \[\frac{1}{2}\]MB
  done clear
  C)
   2 MB          
  done clear
  D)
   MB
  done clear
  View Answer play_arrow

• question_answer17) Voltage V and current\[i\]in AC circuit are given by \[\begin{align}   & V=50\sin (50\,t)\,volt \\  & i=50\,\sin \,\left( 50t+\frac{\pi }{3} \right)mA \\ \end{align}\] The power dissipated in circuit is
  A)
   5.0 W            
  done clear
  B)
   2.5 W
  done clear
  C)
   1.25 W           
  done clear
  D)
   zero
  done clear
  View Answer play_arrow

• question_answer18) The maximum voltage in DC circuit is 282 Volt. The effective voltage in AC circuit will be
  A)
   200 V            
  done clear
  B)
   300 V
  done clear
  C)
   400 V            
  done clear
  D)
   564 V
  done clear
  View Answer play_arrow

• question_answer19) If L, C and R denote inductance, capacitance and resistance respectively, then which of the following combination has the dimension of time?
  A)
   \[\frac{C}{L}\]
  done clear
  B)
   \[\frac{1}{RC}\]
  done clear
  C)
   \[\frac{L}{R}\]
  done clear
  D)
   \[\frac{RL}{C}\]
  done clear
  View Answer play_arrow

• question_answer20) The ratio of momenta of an electron and photon which are accelerated from rest by a potential difference 50 Volt is
  A)
   \[\frac{{{m}_{e}}}{{{m}_{p}}}\]
  done clear
  B)
   \[\sqrt{\frac{{{m}_{e}}}{{{m}_{p}}}}\]
  done clear
  C)
   \[\frac{{{m}_{p}}}{{{m}_{e}}}\]
  done clear
  D)
   \[\sqrt{\frac{{{m}_{p}}}{{{m}_{e}}}}\]
  done clear
  View Answer play_arrow

• question_answer21) A wire of resistance\[18\,\Omega \]is divided into three equal parts. These parts are connected in side of triangle, the equivalent resistance of any two corners of triangle will be
  A)
   18\[\Omega \]          
  done clear
  B)
   9\[\Omega \]
  done clear
  C)
   6\[\Omega \]             
  done clear
  D)
   4\[\Omega \]
  done clear
  View Answer play_arrow

• question_answer22) Two capacitors of capacity 6 \[\mu \]F and 12 \[\mu \]V in series are connected by potential of 150 V. The potential of capacitor of capacity 12 \[\mu \]F will be
  A)
   25 V             
  done clear
  B)
   50 V
  done clear
  C)
   100 V            
  done clear
  D)
   150 V
  done clear
  View Answer play_arrow

• question_answer23) A charged particle enters in a magnetic field whose direction is parallel to velocity of the particle, then the speed of this particle
  A)
   in straight line    
  done clear
  B)
   in coiled path
  done clear
  C)
   in circular path    
  done clear
  D)
   in ellipse path
  done clear
  View Answer play_arrow

• question_answer24) Magnetic intensity for an axial point due to a short bar magnet of magnetic moment M is given by
  A)
   \[\frac{{{\mu }_{0}}}{4\pi }\frac{m}{{{d}^{3}}}\]
  done clear
  B)
   \[\frac{{{\mu }_{0}}M}{4\pi {{d}^{2}}}\]
  done clear
  C)
   \[\frac{{{\mu }_{0}}}{2\pi }\frac{\mu }{{{d}^{3}}}\]
  done clear
  D)
   \[\frac{{{\mu }_{0}}M}{2\pi {{d}^{2}}}\]
  done clear
  View Answer play_arrow

• question_answer25) Which of the following transition gives the photon of minimum frequency?
  A)
   n = 2 to n = 1      
  done clear
  B)
   n = 3 to n = 1
  done clear
  C)
   n = 3 to n = 2     
  done clear
  D)
   n = 4 to n = 3
  done clear
  View Answer play_arrow

• question_answer26)  lonization energy of He+ ion at minimum position is
  A)
   13.6 eV          
  done clear
  B)
   27.2 eV
  done clear
  C)
   54.4 eV          
  done clear
  D)
   68.0 eV
  done clear
  View Answer play_arrow

• question_answer27) The half-life period of a radioactive substance is 3 days. Three fourth of substance decays in
  A)
   3 days            
  done clear
  B)
   6 days
  done clear
  C)
   9 days            
  done clear
  D)
   12 days
  done clear
  View Answer play_arrow

• question_answer28) If the decay constant of a radioactive substance is \[\lambda \], then its half-life is
  A)
   \[\frac{1}{\lambda }{{\log }_{e}}2\]
  done clear
  B)
   \[\frac{1}{\lambda }\]
  done clear
  C)
   \[\lambda {{\log }_{e}}2\]
  done clear
  D)
   \[\frac{\lambda }{{{\log }_{e}}2}\]
  done clear
  View Answer play_arrow

• question_answer29) A galvanometer can be converted into a voltmeter by connecting
  A)
   low resistance in parallel
  done clear
  B)
   low resistance in series
  done clear
  C)
   high resistance in parallel
  done clear
  D)
   high resistance in series
  done clear
  View Answer play_arrow

• question_answer30) A heater coil cut into two equal parts and one part is connected with heater. Now heat generated in heater will be
  A)
   twice            
  done clear
  B)
   half
  done clear
  C)
   one- fourth        
  done clear
  D)
   four times
  done clear
  View Answer play_arrow

• question_answer31) A particle moves along with x-axis. The position\[x\]of particle with respect to time t from origin given by \[x={{b}_{0}}+{{b}_{1}}t+{{b}_{2}}{{t}_{2}}\]. The acceleration of particle is
  A)
   \[{{b}_{0}}\]                
  done clear
  B)
   \[{{b}_{1}}\]
  done clear
  C)
   \[{{b}_{2}}\]                
  done clear
  D)
   \[2{{b}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer32) One end of string of length\[l\]is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v, the net force on the particle (directed towards the centre) is
  A)
   zero              
  done clear
  B)
   \[T-\frac{m{{v}^{2}}}{I}\]
  done clear
  C)
   \[T\]              
  done clear
  D)
   \[T+\frac{m{{v}^{2}}}{I}\]
  done clear
  View Answer play_arrow

• question_answer33) If the kinetic energy of a body is increased 2 times, its momentum will
  A)
   half
  done clear
  B)
   remain unchanged
  done clear
  C)
   be doubled
  done clear
  D)
   increase \[\sqrt{2}\]times
  done clear
  View Answer play_arrow

• question_answer34) The moment of inertia of a solid sphere of mass M and radius R about the tangent on its surface is
  A)
   \[\frac{7}{5}M{{R}^{2}}\]
  done clear
  B)
   \[\frac{4}{5}M{{R}^{2}}\]
  done clear
  C)
   \[\frac{2}{5}M{{R}^{2}}\]           
  done clear
  D)
   \[\frac{1}{2}M{{R}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer35) Satellites A and B are revolving around the orbit of earth. The mass of A is 10 times to mass of B. The ratio of time period \[\left( \frac{{{T}_{A}}}{{{T}_{B}}} \right)\] is
  A)
   \[10\]
  done clear
  B)
   \[1\]
  done clear
  C)
   \[\frac{1}{5}\]
  done clear
  D)
   \[\frac{1}{10}\]
  done clear
  View Answer play_arrow

• question_answer36) A particle of amplitude A is executing simple harmonic motion. When the potential energy of particle is half of its maximum potential energy,   then   displacement   from   its equilibrium position is
  A)
   \[\frac{A}{4}\]                  
  done clear
  B)
   \[\frac{A}{3}\]
  done clear
  C)
   \[\frac{A}{2}\]                  
  done clear
  D)
   \[\frac{A}{\sqrt{2}}\]
  done clear
  View Answer play_arrow

• question_answer37) A simple wave motion represents by\[y=5(\sin 4\pi t+\sqrt{3}\cos 4\pi t)\]. Its amplitude is
  A)
   5                   
  done clear
  B)
   5\[\sqrt{3}\]
  done clear
  C)
   \[10\sqrt{3}\]               
  done clear
  D)
   10
  done clear
  View Answer play_arrow

• question_answer38) A liquid does not wet the sides of a solid, if the angle of contact is
  A)
   obtuse           
  done clear
  B)
   \[90{}^\circ \]
  done clear
  C)
   acute             
  done clear
  D)
   zero
  done clear
  View Answer play_arrow

• question_answer39) Root means square speed of the molecules of ideal gas is\[v\]. If pressure is increased two times at constant temperature, then the rms speed will become
  A)
   \[\frac{v}{2}\]              
  done clear
  B)
   \[v\]
  done clear
  C)
   \[2v\]                 
  done clear
  D)
   \[4v\]
  done clear
  View Answer play_arrow

• question_answer40) 1 mole of gas occupies a volume of 200 ml at 100 mm pressure. What is the volume occupied by two moles of gas at 400 mm pressure and at same temperature?
  A)
   50 mL           
  done clear
  B)
   100 mL
  done clear
  C)
   200 mL          
  done clear
  D)
   400 mL
  done clear
  View Answer play_arrow

• question_answer41) The\[s{{p}^{3}}\]hybridisation is present on the central atom of
  A)
   \[HCHO\]          
  done clear
  B)
   \[BC{{l}_{3}}\]
  done clear
  C)
   \[PC{{l}_{3}}\]            
  done clear
  D)
   \[S{{O}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer42) The number of unit cells in the 5.85 g crystals of\[NaCl\]are
  A)
   \[1.5\times {{10}^{23}}\]        
  done clear
  B)
   \[1.5\times {{10}^{22}}\]
  done clear
  C)
   \[3.0\times {{10}^{22}}\]        
  done clear
  D)
   \[3.0\times {{10}^{23}}\]
  done clear
  View Answer play_arrow

• question_answer43) The oxidation number of sulphur is -1 in
  A)
   \[{{H}_{2}}S\]              
  done clear
  B)
   \[Fe{{S}_{2}}\]
  done clear
  C)
   \[C{{S}_{2}}\]               
  done clear
  D)
   \[C{{u}_{2}}S\]
  done clear
  View Answer play_arrow

• question_answer44) For which of the following metals, the electronic configuration of valence shell is not \[{{d}^{6}}\]?
  A)
   Fe (II)              
  done clear
  B)
  \[Mn\](II)
  done clear
  C)
   Co (III)             
  done clear
  D)
   Ni (IV)
  done clear
  View Answer play_arrow

• question_answer45) 68 g sugar\[({{C}_{12}}{{H}_{22}}{{O}_{11}})\]is dissolved in 1 kg of water. What is the mole fraction of sugar?
  A)
   0.018            
  done clear
  B)
   0.036
  done clear
  C)
   0.0018           
  done clear
  D)
   0.0036
  done clear
  View Answer play_arrow

• question_answer46) The pH of 0.1 M aqueous ammonia \[({{K}_{b}}=1.8\times {{10}^{-5}})\]is.
  A)
   9.13               
  done clear
  B)
   10.13
  done clear
  C)
   11.13             
  done clear
  D)
   12.13
  done clear
  View Answer play_arrow

• question_answer47) From the following mixtures, which is not a buffer (concentration level 0.5 M)?
  A)
   \[C{{H}_{3}}COOH+NaOH(2:1)\]
  done clear
  B)
   \[HCl+N{{H}_{3}}(aq)(1:2)\]
  done clear
  C)
   \[C{{H}_{3}}COOH+NaOH(1:2)\]
  done clear
  D)
   \[HCl+N{{H}_{3}}(2:3)\]
  done clear
  View Answer play_arrow

• question_answer48) How much volume (in litre) of\[3M\,NaOH\]is obtained from 80 g\[NaOH\]? (Atomic mass of \[Na=23u\])
  A)
   2.67               
  done clear
  B)
   1.34
  done clear
  C)
   0.67               
  done clear
  D)
   0.33
  done clear
  View Answer play_arrow

• question_answer49) The initial concentration of sugar solution is 0.12 M. On    doing   fermentation   the concentration of sugar decreases to 0.06 M in 10 h and to 0.045 M in 15 h. The order of the reaction is
  A)
   0.5                  
  done clear
  B)
   1.0
  done clear
  C)
   1.5                  
  done clear
  D)
   2.0
  done clear
  View Answer play_arrow

• question_answer50) For the decomposition of\[{{N}_{2}}O\]and\[{{O}_{2}}\]in presence of at, the velocity constant, k is \[k=5\times {{10}^{11}}{{e}^{-30,000/T}}\] For this, the activation energy is (in kJ\[mo{{l}^{-1}}\])
  A)
   2.494             
  done clear
  B)
   24.94
  done clear
  C)
   249.4             
  done clear
  D)
   2494
  done clear
  View Answer play_arrow

• question_answer51) The following equilibrium establishes on heating 0.2 mole of\[{{H}_{2}}\]and 1.0 mole of sulphur in 1 L vessel at\[90{}^\circ C\]. \[{{H}_{2}}(g)+S(s){{H}_{2}}S(g);\]  \[K=6.8\times {{10}^{-2}}\] The partial pressure of\[{{H}_{2}}S\]in equilibrium state is
  A)
   4.20               
  done clear
  B)
   0.42
  done clear
  C)
   0.21               
  done clear
  D)
   0.042
  done clear
  View Answer play_arrow

• question_answer52) An aqueous solution boils at\[100.2{}^\circ C\]. At which temperature this will freeze. \[({{K}_{b}}=0.5{}^\circ C/m,{{K}_{f}}=1.9{}^\circ C/m)\]
  A)
   \[+0.76\]           
  done clear
  B)
   \[-0.76\]
  done clear
  C)
   \[-0.38\]            
  done clear
  D)
   \[+0.38\]
  done clear
  View Answer play_arrow

• question_answer53) The lowest\[p{{K}_{a}}\]value is for
  A)
   phenol            
  done clear
  B)
  \[m-\]cresol
  done clear
  C)
   o-cresol           
  done clear
  D)
   p-cresol
  done clear
  View Answer play_arrow

• question_answer54) At room temperature, the least stable compound is
  A)
   \[C{{H}_{3}}COCl\]        
  done clear
  B)
   \[HCOCl\]
  done clear
  C)
   \[C{{H}_{3}}COOH\]       
  done clear
  D)
   \[{{(C{{H}_{3}}CO)}_{2}}O\]
  done clear
  View Answer play_arrow

• question_answer55) For the conversion of\[C{{H}_{2}}=C{{H}_{2}}\]into\[HOOC\]. \[C{{H}_{2}}C{{H}_{2}}COOH,\]the minimum number of steps required are
  A)
   2              
  done clear
  B)
   3
  done clear
  C)
   4              
  done clear
  D)
   5
  done clear
  View Answer play_arrow

• question_answer56) Which of the following compounds does not give two isomer compounds on reaction with\[N{{H}_{2}}OH\]?
  A)
   \[C{{H}_{3}}CO{{C}_{2}}{{H}_{5}}\]     
  done clear
  B)
   \[C{{H}_{3}}COC{{H}_{3}}\]
  done clear
  C)
   \[C{{H}_{3}}CHO\]        
  done clear
  D)
   \[PhCOC{{H}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer57) From the following which is not a reactant, reagent or product in Hoffmann reaction?
  A)
   \[RCON{{H}_{2}}\]
  done clear
  B)
   \[RN{{H}_{2}}\]
  done clear
  C)
   \[B{{r}_{2}},O{{H}^{-}}\]
  done clear
  D)
   \[{{H}_{2}}S{{O}_{4}}\]
  done clear
  View Answer play_arrow

• question_answer58) The total number of isomers for cyclic alcohol \[{{C}_{4}}{{H}_{7}}OH\]is
  A)
   2    
  done clear
  B)
   3     
  done clear
  C)
   4    
  done clear
  D)
   5
  done clear
  View Answer play_arrow

• question_answer59) The least stable free radical is
  A)
   \[\overset{\bullet }{\mathop{C}}\,{{H}_{2}}C{{H}_{2}}CH{{(C{{H}_{3}})}_{2}}\]
  done clear
  B)
   \[C{{H}_{3}}\underset{\bullet }{\mathop{C}}\,HCH{{(C{{H}_{3}})}_{2}}\]
  done clear
  C)
   \[C{{H}_{3}}C{{H}_{2}}\underset{\bullet }{\mathop{C}}\,{{(C{{H}_{3}})}_{2}}\]
  done clear
  D)
   \[\overset{\bullet }{\mathop{C}}\,{{H}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer60) The suitable reagent for the reduction of \[{{C}_{2}}{{H}_{5}}COOH\]into\[{{C}_{3}}{{H}_{7}}OH\]is
  A)
   \[B{{H}_{3}}/THF\]and\[{{H}_{3}}{{O}^{+}}\]
  done clear
  B)
   \[NaB{{H}_{4}}\]
  done clear
  C)
   \[Na/EtOH\]
  done clear
  D)
   \[{{H}_{2}}/\]catalyst
  done clear
  View Answer play_arrow

• question_answer61) The blue colour of acidic solution of\[C{{r}_{2}}O_{7}^{2-}\]is not changed into green by
  A)
   \[{{C}_{6}}{{H}_{5}}C{{H}_{2}}OH\]
  done clear
  B)
   \[{{(C{{H}_{3}})}_{2}}CHOH\]
  done clear
  C)
   \[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}C{{H}_{2}}OH\]
  done clear
  D)
   \[{{(C{{H}_{3}})}_{3}}COH\]
  done clear
  View Answer play_arrow

• question_answer62) The reaction of\[{{C}_{2}}{{H}_{5}}Cl\]with\[Li\]and\[CuI\]gives mainly
  A)
   2-butene         
  done clear
  B)
   1, 3-butadiene
  done clear
  C)
   n-butane         
  done clear
  D)
   n-butyl chloride
  done clear
  View Answer play_arrow

• question_answer63) The reagent which does not convert n-butyl chloride into zi-butane is
  A)
   \[Zn,\text{ }HCl\]
  done clear
  B)
   \[LIAl{{H}_{4}}\]
  done clear
  C)
  \[Mg,\]Anhydrous ether,\[{{H}_{2}}O\]
  done clear
  D)
   \[{{B}_{2}}{{H}_{6}}\]in THF
  done clear
  View Answer play_arrow

• question_answer64) The correct order of stability is
  A)
   Pentane < iso-pentane < neo-pentane
  done clear
  B)
   iso-pentane < neo-pentane < pentane
  done clear
  C)
   neo-pentane < iso-pentane < pentane
  done clear
  D)
   Pentane < iso-pentane < iso-pentane
  done clear
  View Answer play_arrow

• question_answer65) The correct order of boiling point of ethyl dimethyl amine , n-butyl amine  and diethyl amine  is
  A)
   \[B>C>A\]          
  done clear
  B)
   \[B>A>C\]
  done clear
  C)
   \[A>B>C\]           
  done clear
  D)
   \[C>B>A\]
  done clear
  View Answer play_arrow

• question_answer66) Which of the following compounds does not give iodoform test?
  A)
   \[C{{H}_{3}}COC{{H}_{2}}COO{{C}_{2}}{{H}_{5}}\]
  done clear
  B)
   \[PhC{{H}_{2}}COC{{H}_{3}}\]
  done clear
  C)
   \[M{{e}_{3}}C.COC{{H}_{3}}\]
  done clear
  D)
   \[C{{H}_{3}}COC{{H}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer67) The species which acts as both nucleophile and electrophile is
  A)
   \[C{{H}_{3}}CN\]
  done clear
  B)
   \[N{{H}_{3}}\]
  done clear
  C)
   \[P{{(C{{H}_{3}})}_{2}}\]
  done clear
  D)
   \[{{H}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer68) The most basic from the following is
  A)
   \[N{{H}_{3}}\]
  done clear
  B)
   \[C{{H}_{3}}N{{H}_{2}}\]
  done clear
  C)
   \[N{{F}_{3}}\]
  done clear
  D)
   \[N{{(Si{{H}_{3}})}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer69) The main product of the reaction of benzene with lithium in liquid ammonia and\[EtOH\]is
  A)
   
  done clear
  B)
   
  done clear
  C)
   
  done clear
  D)
   
  done clear
  View Answer play_arrow

• question_answer70) The rate of free radical chlorination of\[C{{H}_{4}}\]is
  A)
   equal to\[C{{D}_{4}}\]
  done clear
  B)
   double the rate of \[C{{D}_{4}}\]
  done clear
  C)
   12 times the rate of\[C{{D}_{4}}\]
  done clear
  D)
   less than the rate of\[C{{D}_{4}}\]
  done clear
  View Answer play_arrow

• question_answer71) The first ionisation energy difference is maximum for which pair?
  A)
   \[Na,Mg\]          
  done clear
  B)
   \[K,Ca\]
  done clear
  C)
   \[Rb,Sr\]           
  done clear
  D)
   \[Cs,Ba\]
  done clear
  View Answer play_arrow

• question_answer72) The ratio of third Bohr orbit radius and second Bohr orbit radius for the hydrogen atom is
  A)
   0.5                 
  done clear
  B)
   1.5
  done clear
  C)
   0.75               
  done clear
  D)
   2.25
  done clear
  View Answer play_arrow

• question_answer73) The principal quantum number of Mn for those valence shell orbits in which electrons are filled
  A)
   4, 3              
  done clear
  B)
   4, 4
  done clear
  C)
   3, 3              
  done clear
  D)
   5, 4
  done clear
  View Answer play_arrow

• question_answer74) From the generally known oxidation states, the oxidation number is maximum for
  A)
   \[Mn\]             
  done clear
  B)
   \[Cu\]
  done clear
  C)
   \[Sn\]              
  done clear
  D)
   \[Sc\]
  done clear
  View Answer play_arrow

• question_answer75) The number of molecules in 180 g of heavy water are
  A)
   \[6.02\times {{10}^{24}}\]       
  done clear
  B)
   \[6.02\times {{10}^{22}}\]
  done clear
  C)
   \[5.42\times {{10}^{24}}\]       
  done clear
  D)
   \[5.42\times {{10}^{23}}\]
  done clear
  View Answer play_arrow

• question_answer76) Which of the following is reduced by\[{{H}_{2}}{{O}_{2}}\]?
  A)
   \[C{{l}_{2}}\]
  done clear
  B)
   \[{{[Fe{{(CN)}_{6}}]}^{4-}}\]
  done clear
  C)
   \[N{{H}_{2}}OH\]
  done clear
  D)
   \[SO_{3}^{2-}\]
  done clear
  View Answer play_arrow

• question_answer77) The maximum energy molecular orbit filled by electron in nitrogen molecule is/are
  A)
   \[\sigma 2{{p}_{z}}\]
  done clear
  B)
   \[\pi 2{{p}_{x}}\approx \pi 2{{p}_{y}}\]
  done clear
  C)
   \[{{\pi }^{*}}2{{p}_{x}}\approx {{\pi }^{*}}2{{p}_{y}}\]
  done clear
  D)
   \[{{\sigma }^{*}}2{{p}_{z}}\]
  done clear
  View Answer play_arrow

• question_answer78) Which of the following is correct order for density?
  A)
   \[Cs>Rb>K>Na\]
  done clear
  B)
   \[Cs>Rb>Na>K\]
  done clear
  C)
   \[Rb>Cs>K>Na\]
  done clear
  D)
   \[Rb>Cs>Na>K\]
  done clear
  View Answer play_arrow

• question_answer79) The correct order of dipole moment is
  A)
   \[B{{F}_{3}}<{{H}_{2}}S<{{H}_{2}}O\]  
  done clear
  B)
   \[{{H}_{2}}S<B{{F}_{3}}<{{H}_{2}}O\]
  done clear
  C)
   \[{{H}_{2}}O<{{H}_{2}}S<B{{F}_{3}}\]  
  done clear
  D)
   \[{{H}_{2}}O<B{{F}_{3}}<{{H}_{2}}S\]
  done clear
  View Answer play_arrow

• question_answer80) Which of the following bond has minimum bond energy?
  A)
   \[C-H\]
  done clear
  B)
   \[N-H\]
  done clear
  C)
   \[O-H\]
  done clear
  D)
   \[F-H\]
  done clear
  View Answer play_arrow

• question_answer81) The intersection point of the normals drawn at the end points of latusrectum of the parabola\[{{x}^{2}}=-2y\]is
  A)
   \[\left( -\frac{1}{2},-\frac{3}{2} \right)\]
  done clear
  B)
   \[\left( \frac{1}{2},-\frac{3}{2} \right)\]
  done clear
  C)
   \[(0,-1)\]
  done clear
  D)
   \[\left( 0,-\frac{3}{2} \right)\]
  done clear
  View Answer play_arrow

• question_answer82) The equation whose roots are reciprocal of the roots of the equation\[a{{x}^{2}}+bx+c=0,\]is
  A)
   \[b{{x}^{2}}+cx+a=0\]   
  done clear
  B)
   \[b{{x}^{2}}+ax+c=0\]
  done clear
  C)
   \[c{{x}^{2}}+ax+b=0\]   
  done clear
  D)
   \[c{{x}^{2}}+bx+a=0\]
  done clear
  View Answer play_arrow

• question_answer83) If in the expansion of\[{{\left( 3x-\frac{2}{{{x}^{2}}} \right)}^{15}},\]rth term is independent of\[x,\]then value of r is
  A)
   11     
  done clear
  B)
   10    
  done clear
  C)
   9     
  done clear
  D)
   12
  done clear
  View Answer play_arrow

• question_answer84) If\[f(x)=\left| \begin{matrix}    1+a & 1-ax & 1+a{{x}^{2}}  \\    1+b & 1+bx & 1+b{{x}^{2}}  \\    1+c & 1+cx & 1+c{{x}^{2}}  \\ \end{matrix} \right|,\]where\[a,b,c\] are non-zero Constants, then value of\[f(10)\] is
  A)
   \[10(b-a)(c-a)\]
  done clear
  B)
   \[100(b-a)(c-b)(a-c)\]
  done clear
  C)
   \[100\,abc\]
  done clear
  D)
   0
  done clear
  View Answer play_arrow

• question_answer85) If\[^{n}{{C}_{12}}{{=}^{n}}{{C}_{8}},\]then value of\[^{n}{{C}_{19}}\]is
  A)
   1                
  done clear
  B)
   20
  done clear
  C)
   210              
  done clear
  D)
   1540
  done clear
  View Answer play_arrow

• question_answer86) If\[\omega \]is a complex cube root of unity and\[A=\left[ \begin{matrix}    \omega  & 0  \\    0 & \omega   \\ \end{matrix} \right],\]then\[{{A}^{50}}\]is
  A)
   \[{{\omega }^{2}}A\]
  done clear
  B)
   \[\omega A\]
  done clear
  C)
   \[A\]
  done clear
  D)
   \[0\]
  done clear
  View Answer play_arrow

• question_answer87) If sum of\[n\]terms of an AP is\[2n+3{{n}^{2}},\]then rth term is
  A)
   \[2r+3{{r}^{2}}\]           
  done clear
  B)
   \[3{{r}^{2}}-4r+1\]
  done clear
  C)
   \[6r-1\]             
  done clear
  D)
   \[4r+1\]
  done clear
  View Answer play_arrow

• question_answer88) If A and B are square matrices of order\[3\times 3,\] then which of the following is true?
  A)
   \[AB=0\Rightarrow A=O\]or\[B=O\]
  done clear
  B)
   \[det(2AB)=8\text{ (}detA)\text{ (}detB)\]
  done clear
  C)
   \[{{A}^{2}}-{{E}^{2}}=(A+B)(A-B)\]
  done clear
  D)
   \[det(A+B)=det(A)+det(B)\]
  done clear
  View Answer play_arrow

• question_answer89) If geometric mean and harmonic mean between two different numbers are 12 and \[\frac{48}{5}\]respectively, then one number is
  A)
   4                
  done clear
  B)
   6
  done clear
  C)
   8                
  done clear
  D)
   10
  done clear
  View Answer play_arrow

• question_answer90) Let a, b, c are in GP and 4a,5b,4c are in AP such that\[a+b+c=70,\]then value of\[b\]is
  A)
   5     
  done clear
  B)
   10     
  done clear
  C)
   15     
  done clear
  D)
   20
  done clear
  View Answer play_arrow

• question_answer91) The value of integral\[\int_{0}^{4}{|x-1|}dx\] is
  A)
   4      
  done clear
  B)
   5       
  done clear
  C)
   7      
  done clear
  D)
   9
  done clear
  View Answer play_arrow

• question_answer92) If\[\frac{x-1}{1+i}+\frac{y-1}{1-i}=i,\]where\[x\]and y are real numbers and\[i=\sqrt{-1},\]then
  A)
   \[x=0\]            
  done clear
  B)
   \[x<0\]
  done clear
  C)
   \[x>0\]            
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer93) If a pair of two fair dice is thrown, then the probability of getting the sum 5 on both dice is
  A)
   \[\frac{5}{36}\]
  done clear
  B)
   \[\frac{1}{12}\]
  done clear
  C)
   \[\frac{1}{18}\]
  done clear
  D)
   \[\frac{1}{9}\]
  done clear
  View Answer play_arrow

• question_answer94) If a fair coin is tossed 20 times and let we get head n times, then probability that 21 is odd, is
  A)
   \[\frac{1}{2}\]
  done clear
  B)
   \[\frac{1}{6}\]
  done clear
  C)
   \[\frac{5}{8}\]
  done clear
  D)
   \[\frac{7}{8}\]
  done clear
  View Answer play_arrow

• question_answer95) If\[{{x}_{r}}=\cos \left( \frac{\pi }{{{2}^{r}}} \right)+i\sin \left( \frac{\pi }{{{2}^{r}}} \right),\]then value of\[{{x}_{1}}\,{{x}_{2}}\,\,{{x}_{3}}....\]is
  A)
   \[i\]
  done clear
  B)
   \[1\]
  done clear
  C)
   \[-1\]
  done clear
  D)
   \[-i\]
  done clear
  View Answer play_arrow

• question_answer96) If\[{{\left( \frac{1+\cos \phi +i\sin \phi }{1+\cos \phi -i\sin \phi } \right)}^{n}}=u+iv,\]where u and v are real numbers, then u is
  A)
   \[n\cos \phi \]
  done clear
  B)
   \[\cos n\phi \]
  done clear
  C)
   \[\cos \left( \frac{n\phi }{2} \right)\]
  done clear
  D)
   \[\sin \left( \frac{n\phi }{2} \right)\]
  done clear
  View Answer play_arrow

• question_answer97) If square root of \[-7+24i\] is \[x+iy,\] then \[x\] is
  A)
   ±1              
  done clear
  B)
   ± 2
  done clear
  C)
   ±3               
  done clear
  D)
   ± 4
  done clear
  View Answer play_arrow

• question_answer98) If \[{{\tanh }^{-1}}(x-iy)=\frac{1}{2}{{\tanh }^{-1}}\left( \frac{2x}{1+{{x}^{2}}+{{y}^{2}}} \right)\] \[+\frac{i}{2}{{\tan }^{-1}}\left( \frac{2y}{1-{{x}^{2}}-{{y}^{2}}} \right)x,y\in R,\] then \[{{\tanh }^{-1}}(iy)\] is
  A)
    \[2\text{ }tan{{h}^{-1}}(y)\]        
  done clear
  B)
    \[-2\text{ }tan{{h}^{-1}}(y)\]
  done clear
  C)
    \[\text{i }ta{{n}^{-1}}y\]          
  done clear
  D)
    \[\text{-i }ta{{n}^{-1}}(y)\]
  done clear
  View Answer play_arrow

• question_answer99) If \[f:R\to R\] is defined as \[f(x)={{(1-x)}^{1/3}}\] then \[{{f}^{-1}}(x)\] is
  A)
    \[{{(1-x)}^{-1/3}}\]
  done clear
  B)
    \[{{(1-x)}^{3}}\]
  done clear
  C)
    \[1-{{x}^{3}}\]
  done clear
  D)
    \[1-{{x}^{1/3}}\]
  done clear
  View Answer play_arrow

• question_answer100) If \[{{x}^{y}}={{e}^{x-y}},x>0,\] then value of \[\frac{dy}{dx}\] at (1,1) is
  A)
   0
  done clear
  B)
    \[\frac{1}{2}\]
  done clear
  C)
   1
  done clear
  D)
   2
  done clear
  View Answer play_arrow

• question_answer101) The value of \[\underset{x\to 0}{\mathop{\lim }}\,\frac{(1-\cos 2x)}{{{x}^{2}}}\]is
  A)
   doesn't exist       
  done clear
  B)
   infinite
  done clear
  C)
   0                  
  done clear
  D)
   2
  done clear
  View Answer play_arrow

• question_answer102) The value of differentiation of\[{{e}^{{{x}^{2}}}}\]w.r.t. to \[{{e}^{2x-1}}\]at\[x=1\]is
  A)
   e     
  done clear
  B)
   0      
  done clear
  C)
   \[{{e}^{-1}}\]     
  done clear
  D)
   1
  done clear
  View Answer play_arrow

• question_answer103) If function\[f(x),x\in R\]is differentiable and \[f(1)=1,\]then value of\[\underset{x\to 0}{\mathop{\lim }}\,\frac{(1-\cos 2x)}{{{x}^{2}}}\]is
  A)
   0                 
  done clear
  B)
   1
  done clear
  C)
   \[f'(1)\]            
  done clear
  D)
   \[\infty \]
  done clear
  View Answer play_arrow

• question_answer104) The value of integral \[\int_{0}^{2a}{\frac{f(x)}{f(x)+f(2a-x)}}dx,\]where\[f(x)\]is a continuous function, is
  A)
   0                
  done clear
  B)
   1
  done clear
  C)
   \[a\]                
  done clear
  D)
   \[2a\]
  done clear
  View Answer play_arrow

• question_answer105) The area of the region bounded by the curves \[y=ex,\text{ y}=lo{{g}_{e}}x\]and lines\[x=1,\text{ }x=2\]is
  A)
   \[{{(e-1)}^{2}}\]
  done clear
  B)
   \[{{e}^{2}}-e+1\]
  done clear
  C)
   \[{{e}^{2}}-e+1-2lo{{g}_{e}}2\]
  done clear
  D)
   \[{{e}^{2}}+e-2lo{{g}_{e}}2\]
  done clear
  View Answer play_arrow

• question_answer106) If\[f(x)=sin\text{ }x+cos\text{ }x+1\]and \[g(x)={{x}^{2}}+x,\text{ }x\in R,\]then value of\[fog(x)\]at \[x=0\]is
  A)
   0      
  done clear
  B)
   1        
  done clear
  C)
   2     
  done clear
  D)
   3
  done clear
  View Answer play_arrow

• question_answer107) The maximum value of function \[f(x)=\sin x(1+\cos x),x\in R\]is
  A)
   \[\frac{{{3}^{3/2}}}{4}\]
  done clear
  B)
   \[\frac{{{3}^{5/3}}}{4}\]
  done clear
  C)
   \[\frac{3}{2}\]
  done clear
  D)
   \[\frac{{{3}^{7/5}}}{4}\]
  done clear
  View Answer play_arrow

• question_answer108) The normal at point (1,1) to the curve\[{{y}^{2}}={{x}^{3}}\]is parallel to the line
  A)
   \[3x-y-2=0\]    
  done clear
  B)
   \[2x+3y-7=0\]
  done clear
  C)
   \[2x-3y+1=0\]   
  done clear
  D)
   \[2y-3x+1=0\]
  done clear
  View Answer play_arrow

• question_answer109) Function\[f(x)=|x-1|+|x-2|,x\in R\]is
  A)
   differentiable everywhere in R
  done clear
  B)
   except\[x=1\]and\[x=2\]differentiable everywhere in R
  done clear
  C)
   not continuous at\[x=1\]and\[x=2\]
  done clear
  D)
   increasing in\[R\]
  done clear
  View Answer play_arrow

• question_answer110) If\[f(1)=2\]and\[f'(1)=1,\]then the value of\[\underset{x\to 1}{\mathop{\lim }}\,\frac{2x-f(x)}{x-1}\]is
  A)
   \[-1\]            
  done clear
  B)
   0
  done clear
  C)
   \[1\]              
  done clear
  D)
   2
  done clear
  View Answer play_arrow

• question_answer111) The distance of the point P (1,2,3) from the line which passes through the point A (4,2,2) and parallel to the vector\[2\hat{i}+3\hat{j}+6\hat{k},\]is
  A)
   \[\sqrt{10}\]     
  done clear
  B)
   \[\sqrt{7}\]
  done clear
  C)
   \[\sqrt{5}\]               
  done clear
  D)
   \[1\]
  done clear
  View Answer play_arrow

• question_answer112) Let\[\overrightarrow{a}=2\hat{i}+\hat{k},\overrightarrow{b}=\hat{i}+\hat{i}+\hat{k}\]and\[\overrightarrow{c}=4\hat{i}-3\hat{j}+7\hat{k}\]. If r is a vector such that\[\overrightarrow{r}\times \overrightarrow{b}=\overrightarrow{c}\times \overrightarrow{b}\] and\[\overrightarrow{r}.\overrightarrow{a}=0,\]then value of\[\overrightarrow{r}.\overrightarrow{b}\]is
  A)
   7                
  done clear
  B)
   \[-7\]
  done clear
  C)
   \[-5\]               
  done clear
  D)
   5
  done clear
  View Answer play_arrow

• question_answer113) A unit vector which is coplanar with \[\hat{i}+\hat{j}+2\hat{k}\]and\[\hat{i}+2\hat{j}+\hat{k}\]and perpendicular to \[\hat{i}+\hat{j}+\hat{k},\] is
  A)
   \[\frac{(-\hat{j}+\hat{k})}{\sqrt{2}}\]
  done clear
  B)
   \[\frac{(\hat{k}-\hat{i})}{\sqrt{2}}\]
  done clear
  C)
   \[\frac{(\hat{i}-\hat{j})}{\sqrt{2}}\]
  done clear
  D)
   \[\frac{(\hat{i}-\hat{k})}{\sqrt{2}}\]
  done clear
  View Answer play_arrow

• question_answer114) If a line is inclined at\[45{}^\circ \]to both x-axis and\[y-\]axis, then the angle at which it is inclined to z-axis is
  A)
   \[45{}^\circ \]             
  done clear
  B)
   \[60{}^\circ \]
  done clear
  C)
   \[30{}^\circ \]              
  done clear
  D)
   \[90{}^\circ \]
  done clear
  View Answer play_arrow

• question_answer115) The equation of plane which passes through the point\[(1,2,-1)\]and parallel to the plane \[x-y+2z=0\]is
  A)
   \[x-y+2z-3=0\]  
  done clear
  B)
   \[x-y+2z+3=0\]
  done clear
  C)
   \[x-y+2z+6=0\] 
  done clear
  D)
   \[x-y+2z-7=0\]
  done clear
  View Answer play_arrow

• question_answer116) Let a plane passes through the point P(-1, -1,1) and also passes through a line joining the points Q (0,1,1) and R(Q,0,2). Then, the distance of plane from the point (0,0,0) is
  A)
   3                
  done clear
  B)
   0
  done clear
  C)
   \[1/\sqrt{6}\]             
  done clear
  D)
   \[2/\sqrt{6}\]
  done clear
  View Answer play_arrow

• question_answer117) If\[f(x)\]and\[g(x),x\in R\]are continuous functions, then value of integral \[\int_{-\pi /2}^{\pi /2}{[\{f(x)+f(-x)\}\{g(x)-g(-x)\}]}\,dx\]is
  A)
   \[\pi \]                
  done clear
  B)
   \[\pi /2\]
  done clear
  C)
   \[1\]                
  done clear
  D)
   0
  done clear
  View Answer play_arrow

• question_answer118) The equation of circle which touches the\[x-\]axis and 7-axis at points (1, 0) and (0, 1) respectively, is
  A)
   \[{{x}^{2}}+{{y}^{2}}-4y+3=0\]
  done clear
  B)
   \[{{x}^{2}}+{{y}^{2}}-2y-2=0\]
  done clear
  C)
   \[{{x}^{2}}+{{y}^{2}}-2x-27+2=0\]
  done clear
  D)
   \[{{x}^{2}}+{{y}^{2}}-2x-2y+1=0\]
  done clear
  View Answer play_arrow

• question_answer119) If lines\[4x+3y=1,\text{ }y-x=5\]and\[kx+5y=1\]are concurrent, then value of k is
  A)
   0              
  done clear
  B)
   1
  done clear
  C)
   3               
  done clear
  D)
   7
  done clear
  View Answer play_arrow

• question_answer120) The equation\[{{y}^{2}}-8y-x+19=0\]represents
  A)
   a parabola whose focus is\[\left( \frac{1}{4},0 \right)\]and directrix is\[x=-\frac{1}{4}\]
  done clear
  B)
   a parabola whose vertex is (3, 4) and directrix is\[x=\frac{11}{4}\]
  done clear
  C)
   a parabola whose focus is\[\left( \frac{13}{4},4 \right)\]and vertex is (0, 0)
  done clear
  D)
   a curve which is not a parabola
  done clear
  View Answer play_arrow