Current Affairs 6th Class

Category : 6th Class

Knowing our Numbers

·                      

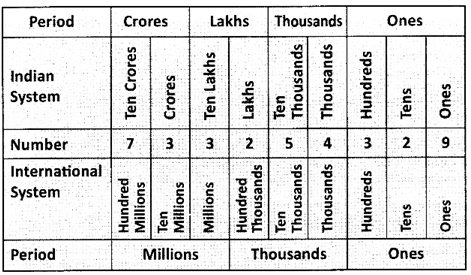
Indian System: 73, 32, 54,329

International System: 733,254,329

Note:    A Comma is inserted each period in both the systems.

• To write numbers in the Indian System, we put a comma after three digits from the right. and then after every two digits.

e.g., 5340769 = 53, 40,769

• To write numbers in the International System, we put a comma after every three digits, starting from the right.

e.g., 5340769 = 5,340,769

• Face value of a digit:

The face value of a digit is the value of the digit itself.

e.g. In 7308, the face value of 7 is 7.

• Place value of a digit:

Place value = Face value \[\times \]Value of its place in the place value chart

e.g., (1) In 39065, the face value of 9 is 9 and the place value of 9 is 9 x 1000 = 9000.

e.g., (2) In 7308, the face value of 3 is 3; while its place value is 300.

Note: Place value of zero(0) at any place is always zero. Thus, the face value and the place value of zero are 0.

• Expanded form of a number:

To write a number in expanded form, start from the left-most digit. Write the digit in the given number followed by as many zeroes as the number of digits to its right. Place a + sign before writing the next digit. Continue this until the right-most digit is written.

e.g.. The expanded form of

906352146 = 900000000 + 00000000 + 6000000 + 300000 + 50000 + 2000 + 100 +40+6

Note: To write the smallest of \[\mathbf{'n'}\]digits (other than 1), write 1 followed by (n - 1) zeroes. To write the largest number of \[\mathbf{'n'}\] digits, write \[\mathbf{'n'}\] 9 s.

• Comparing numbers:

(i) Count the number of places. The number with more number of places is greater and that with less places is smaller.

(ii) If the number of places is equal then compare the value of the digit present from place to place from left to right in both the numbers. The number with greater value is greater.

• Numbers in increasing order are in ascending order while numbers in decreasing order are in descending order.

• Numbers can be arranged in ascending or descending orders.

• The number which is one more than the given number is called its successor. Every number has a successor.

• The number which is one less than the given number is called its predecessor. Every number other than zero has a predecessor.

• There are seven symbols to represent numbers of Hindu-Arabic system in Roman numeration.

• While writing numbers in Roman System there are certain rules to be followed.

Rule 1: If a symbol is repeated, its value is added as many times as it occurs.

Note: A Symbol is never repeated for more than three times. The symbols V,L and D are never repeated i.e., only I ,X,C and M can be repeated.

Rule 2: When a symbol of smaller value is written to the right of a symbol of greater value, its value is added to the value of the greater symbol.

e.g., XI =10+1 =11; LXV= 50+10+5=65

Rule 3: When a symbol of smaller value is written to the left of a symbol of greater value, its value is subtracted from the value of the greater symbol.

e.g., XC=100-10=90; IV=5-1 =4

Note: The symbols V,L and D are n ever subtracted.\[\mathbf{'I'}\]Can be subtracted from V and X only once.\[\mathbf{'X'}\] can be subtracted from L and C only once.\[\mathbf{'C'}\]can be subtracted from D and M only once.

With the help of the symbols I, V, X, L and C, we can write numbers upto 399.

Rule4: When a smaller numeral is placed between two larger numerals, it is always subtracted from the larger numeral immediately following it.

e.g., CXIV = 100 + 10 + (5 - 1) = 114.

Rule 5: When a bar is placed over a numeral, it is multiplied by 1000.

e.g., \[\overline{V}\]= 5000, z\[\overline{L}\]= 50000, \[\overline{IV}\]= 4000.

• Approximating a quantity to a required accuracy is called estimation.

• Estimating is done by rounding off the numbers involved and getting a quick, rough answer.

e.g., 4117 can be approximated to 4100 (to the nearest hundred)

4117 can be approximated to 4000 (to the nearest thousand)

• To avoid confusion in the problems in which a number of operations are carried out, we use Brackets.