Playing with Numbers
- A factor of a number is an exact divisor of that number.
- A number is said to be a multiple of any of its factors.
e.g.. We know that 35 = 1\[\times \]35 and 35 = 5 \[\times \] 7.
This shows that each of the numbers 1, 5, 7 and 35 divides 35 exactly.
Therefore 1, 5, 7 and 35 are all factors of 35 and 35 is a multiple of each one of the numbers
1, 5, 7 and 35.
- All multiples of 2 are called even numbers.
e.g., 2, 4, 6,8,10, etc.
- Numbers which are not multiples of 2 are called odd numbers.
e.g., 1,3,5,7,9,11, etc.
- Each of the numbers which has exactly two distinct factors, namely 1 and itself is called a
prime number.
e.g., 2,3,5,7,11,13,17,19,23,29 etc.
- Numbers having more than two factors are known as composite numbers.
e.g., 4, 6, 8,9,10 etc.
Note: (i) 1 is neither prime composite. (since 1=1, the two factors are not distinct.)
(ii) 2 is the lowest prime numbers.
(iii) 2 is the only even prime number. (All other even number are composite numbers.)
- Two consecutive prime numbers differing by 2 are known as twin-primes.
e.g., (i) 3, 5 (ii) 5, 7 (iii) 11, 13 etc.
A set of three consecutive prime numbers, differing by 2, is called a prime triplet.
An example of prime triplet is (3, 5, 7).
- If the sum of all the factors of a number is twice the number then the number is called a perfect number,
e.g., 6 is a perfect number, since the factors of 6 are 1,2,3,6 and (1 + 2 + 3 + 6) = (2 x 6).
- Two numbers are said to be co-prime if they do not have a common factor other than 1.
e.g., (i) 2, 3 (ii) 3, 4 (iii) 8, 15
Note: (i) Two prime numbers are always co – prime.
(ii) Two co – prime need not be prime numbers.
e.g., 6, 7 are co-primes, while 6 is not a prime number
- Every even number greater than 4 can be expressed as the sum of two odd prime numbers.
e.g., (i) 6 = 3 + 3 (ii) 8 = 3+5
Tests of divisibility of numbers
- Test of divisibility by 2:
- A number is divisible by 2, if its units digit is 0,2,4,6 or 8.
e.g., 42,84,120,1456,568 etc. are divisible by 2.
- Test of divisibility by 3:
A number is divisible by
more...
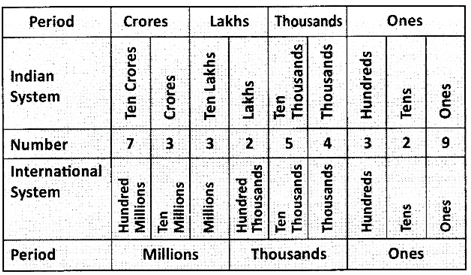 Indian System: 73, 32, 54,329
International System: 733,254,329
Note: A Comma is inserted each period in both the systems.
Indian System: 73, 32, 54,329
International System: 733,254,329
Note: A Comma is inserted each period in both the systems.

