Conformational Isomerism
Category : JEE Main & Advanced
(1) Definition : The different arrangement of atoms in a molecule which can be obtained due to rotation about carbon-carbon single bond are called conformational isomers (conformers) or rotational isomers (rotamers). This type of isomerism is found in alkanes and cycloalkanes and their substituted derivatives.
It may be noted that rotation around a \[C-C\] sigma bond is not completely free. It is in fact hindered by an energy barrier of 1 to 20 kJ \[mo{{l}^{-1}}\] in different bonds. There is a possibility of weak repulsive interactions between the bonds or electron pairs of the bonds on adjacent carbon atoms. Such type of repulsive interaction is known as torsional strain.
(2) Difference between conformation and configuration : The term conformation should not be confused with the configuration which relates to those spatial arrangements of the atoms of a molecule that can be changed only by the breaking and making of bonds whereas the spatial arrangements in conformation are changed simply by rotation about a single bond.
(3) Representation of conformations : Conformers can be represented in two simple ways. These are : (i) Saw horse representation and (ii) Newman projection
(i) Saw horse representation : In this projection, the molecule is viewed along the axis of the model from an oblique angle. The central carbon-carbon bond (\[C-C\]) is draw as a straight line slightly tilted to right for the sake of clarity. The front carbon is shown as the lower left hand carbon and the rear carbon is shown as the upper right hand carbon. The three bonds around each carbon atom \[(C-H\] in ethane or \[C-C\] in higher alkanes) are shown by three lines.
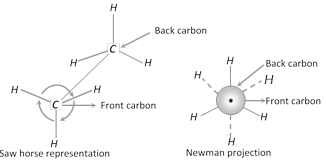
(ii) Newman projection : This is a simple method to represent the conformations. In this method, the molecule is viewed from the front along the carbon-carbon bond axis. The two carbon atoms forming the s-bond are represented by two circles; one behind the other so that only the front carbon is seen. The front carbon atom is shown by a point whereas the carbon further from the eye is represented by the circle. Therefore, the \[C-H\] bonds of the front carbon are depicted from the centre of the circle while \[C-H\] bonds of the back carbon are drawn from the circumference of the circle at an angle of \[{{120}^{o}}\] to each other.
(4) Conformation in alkanes
(i) Conformations of ethane : When one of the carbon atom is kept fixed and other is rotated about \[C-C\] bond an infinite numbers of isomers are possible. Out of all the conformations for ethane, only two extreme conformations are important and these are:
(a) Staggered conformation
(b) Eclipsed conformation
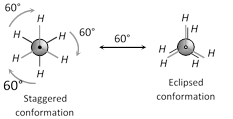
Staggered conformation of ethane is more stable than eclipsed.
(ii) Conformations of propane : The next higher member in alkane series, propane \[(C{{H}_{3}}-C{{H}_{2}}-C{{H}_{3}})\] also has two extreme conformations, the energy barrier in propane is \[14\,kJ\,mo{{l}^{-1}}\], which is slightly higher than that in ethane.

(iii) Conformations of butane : As the alkane molecule becomes larger, the conformation situation becomes more complex. In butane \[(C{{H}_{3}}-C{{H}_{2}}-C{{H}_{2}}-C{{H}_{3}})\], for example, the rotation about the single bond between two inner atoms (\[{{C}_{2}}\] and\[{{C}_{3}}\]) is considered. In this case, all the staggered as well as eclipsed conformations will not have same stability and energy because of different types of interaction between \[C-C\](of methyl) and \[C-H\] bonds.
The lowest energy conformation will be the one, in which the two methyl groups are as far apart as possible i.e., \[{{180}^{o}}\]away form each other.
This conformation will be maximum staggered, most stable and is called anti or trans conformation (marked I). Other conformations can be obtained by rotating one of the \[{{C}_{2}}\] or \[{{C}_{3}}\] carbon atoms through an angle of \[{{60}^{o}}\] as shown ahead.
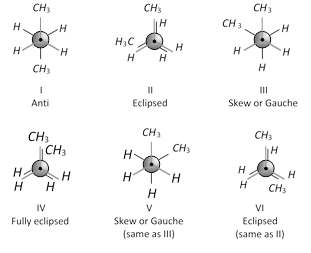
As is clear from the above Newman projection the Gauche or Skew conformations (III and V) are also staggered. However, in these conformations, the methyl groups are so close that they repel each other. This repulsion causes gauche conformations, to have about \[3.8\,\,kJ\,mo{{l}^{-1}}\] more energy than anti conformation. This conformations II and VI are eclipsed conformations. These are unstable because of repulsions. These are \[16\,kJ\,mo{{l}^{-1}}\] less stable than anti conformation. Conformation IV is also eclipsed and it is least stable having energy \[19\,kJ\,mo{{l}^{-1}}\] more than anti conformation. This is because of repulsion between methyl-methyl groups which are very closed together. It is called fully eclipsed conformation.
The order of stability of these conformations is, Anti > Skew or Gauche > Eclipsed > Fully eclipsed.
(5) Conformations in cycloalkanes
(i) Stability of cycloalkanes : Compounds with three and four membered rings are not as stable as compounds with five or six membered rings.
The German chemist Baeyer was the first to suggest that the instability of these small rings compounds was due to angle strain. This theory is known as Baeyer-strain theory.
Baeyer strain theory was based upon the assumption that when an open chain organic compound having the normal bond angle \[{{109.5}^{o}}\] is convert into a cyclic compound, a definite distortion of this normal angle takes place leading to the development of a strain in the molecule.
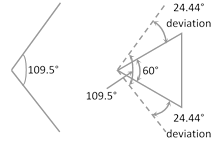
Baeyer assumed that cyclic rings are planar. Assuming that the rings are planar, the amount of strain in various cycloalkanes can be expressed in terms of angle of deviation (d).
\[d=\frac{1}{2}\left[ 109.5-\frac{2(n-2)}{n}\times 90 \right]\] or \[d=\frac{1}{2}[109.5-\alpha ]\]
Where \[n=\] number of carbon-carbon bonds in cycloalkane ring; \[\alpha =\] inner bond angle in the cycloalkane ring.
\[\text{Angle strain}\propto d\propto \frac{\text{1}}{\text{inner angle}}\];
\[\text{Stability }\propto \frac{\text{1}}{d}\propto \text{inner}\,\text{angle(}\alpha \text{)}\]
Now let us take the case of three to eight membered cyclic compounds.
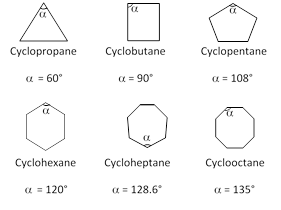
The positive and negative values of (d) indicate whether the inner angle is less than or more than the normal tetrahedral value.
Beayer thus predicted that a five membered ring compound would be the most stable. He also predicted that six membered ring compounds would be less stable and as the cyclic compounds become larger than five membered ring, then they would become less and less stable.
Contrary to what Baeyer predicted, however cyclohexane is more stable than cyclopentane. Furthermore, cyclic compounds do not become less and less stable as the number of sides increase. Thus Baeyer strain theory is applicable only to cyclopropane, cyclobutane and cyclopantane.
The mistake that Baeyer made was to assume that all cyclic compounds are planar. But only cyclopropane is planar and other cycloalkanes are not planar. Cyclic compounds twist and bend in order to achieve structure that minimises the three different kinds of strain and that can destabilise a cyclic compound.
(a) Angle strain is the strain that results when the bond angle is different from desired tetrahedral bond angle of \[{{109.5}^{o}}\].
(b) Torsional strain is caused by repulsion of the bonding electrons of one substituent with bonding electrons of a nearby substituent.
(c) Steric strain is caused by atoms or groups of atoms approaching each other too closely.
(ii) Conformation of cyclohexane : Despite Baeyer’s prediction that five-membered cyclic compounds would be the most stable, the six membered cyclic compound is the most stable. Six membered cyclic compound are most stable because they can exist in a conformation that is almost completely free of strain. This conformation is called the chair conformation. In a chair conformation of cyclohexane all bond angles are \[{{109.38}^{o}}\] which is very close to the \[{{109.5}^{o}}\] and all the adjacent carbon-hydrogen bonds are staggered.
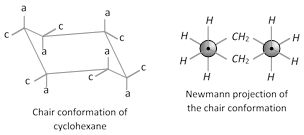
\[C-1,\,C-3\] and \[C-5\] axial bonds are above the plane
\[C-2,\,C-4\] and \[C-6\] axial bonds are below the plane
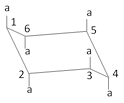
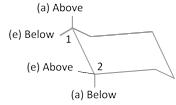
(a) Thus \[C-1\] equatorial and \[C-2\] equatorial bonds are trans.
(b) \[C-1\] axial and \[C-2\] equatorial will be cis.

Chair > twist boat > boat > half chair.
You need to login to perform this action.
You will be redirected in
3 sec
