-
question_answer1)
Two bodies M and N of equal masses are suspended from two separate massless springs of force constants k1 and k2 respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude M to that of N is [IIT-JEE 1988; MP PET 1997, 2001; MP PMT 1997; BHU 1998; Pb. PMT 1998; MH CET 2000, 03; AIEEE 2003]
A)
\[\frac{{{k}_{1}}}{{{k}_{2}}}\] done
clear
B)
\[\sqrt{\frac{{{k}_{1}}}{{{k}_{2}}}}\] done
clear
C)
\[\frac{{{k}_{2}}}{{{k}_{1}}}\] done
clear
D)
\[\sqrt{\frac{{{k}_{2}}}{{{k}_{1}}}}\] done
clear
View Solution play_arrow
-
question_answer2)
A mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k1 and k2 respectively. When set into vertical vibrations, the period will be [MP PMT 2001]
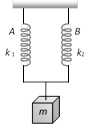
A)
\[2\pi \sqrt{\left( \frac{m}{{{k}_{1}}{{k}_{2}}} \right)}\] done
clear
B)
\[2\pi \sqrt{m\left( \frac{{{k}_{1}}}{{{k}_{2}}} \right)}\] done
clear
C)
\[2\pi \sqrt{\left( \frac{m}{{{k}_{1}}-{{k}_{2}}} \right)}\] done
clear
D)
\[2\pi \sqrt{\left( \frac{m}{{{k}_{1}}+{{k}_{2}}} \right)}\] done
clear
View Solution play_arrow
-
question_answer3)
A spring has a certain mass suspended from it and its period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is now [MP PET 1995]
A)
\[\frac{T}{2}\] done
clear
B)
\[(3/2)k\] done
clear
C)
\[6k\] done
clear
D)
\[\sqrt{{{K}_{1}}}:\sqrt{{{K}_{2}}}\] done
clear
View Solution play_arrow
-
question_answer4)
Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are suspended together by a massless spring of constant k. When the masses are in equilibrium, \[{{m}_{1}}\] is removed without disturbing the system. Then the angular frequency of oscillation of \[{{m}_{2}}\] is
A)
\[\sqrt{\frac{k}{{{m}_{1}}}}\] done
clear
B)
\[\sqrt{\frac{k}{{{m}_{2}}}}\] done
clear
C)
\[\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}\] done
clear
D)
\[\sqrt{\frac{k}{{{m}_{1}}{{m}_{2}}}}\] done
clear
View Solution play_arrow
-
question_answer5)
In arrangement given in figure, if the block of mass m is displaced, the frequency is given by [BHU 1994; Pb. PET 2001]
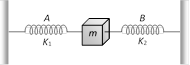
A)
\[n=\frac{1}{2\pi }\sqrt{\left( \frac{{{k}_{1}}-{{k}_{2}}}{m} \right)}\] done
clear
B)
\[n=\frac{1}{2\pi }\sqrt{\left( \frac{{{k}_{1}}+{{k}_{2}}}{m} \right)}\] done
clear
C)
\[n=\frac{1}{2\pi }\sqrt{\left( \frac{m}{{{k}_{1}}+{{k}_{2}}} \right)}\] done
clear
D)
\[n=\frac{1}{2\pi }\sqrt{\left( \frac{m}{{{k}_{1}}-{{k}_{2}}} \right)}\] done
clear
View Solution play_arrow
-
question_answer6)
Two identical spring of constant K are connected in series and parallel as shown in figure. A mass m is suspended from them. The ratio of their frequencies of vertical oscillations will be [MP PET 1993; BHU 1997]
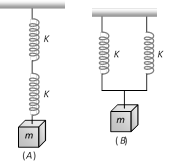
A)
2 : 1 done
clear
B)
1 : 1 done
clear
C)
1 : 2 done
clear
D)
4 : 1 done
clear
View Solution play_arrow
-
question_answer7)
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are \[{{K}_{1}}\] and \[{{K}_{2}}\]. The time period of the suspended mass will be [CBSE PMT 1990; Pb. PET 2002]
A)
\[T=2\pi \sqrt{\left( \frac{m}{{{K}_{1}}+{{K}_{2}}} \right)}\] done
clear
B)
\[T=2\pi \sqrt{\left( \frac{m}{{{K}_{1}}+{{K}_{2}}} \right)}\] done
clear
C)
\[T=2\pi \sqrt{\left( \frac{m({{K}_{1}}+{{K}_{2}})}{{{K}_{1}}{{K}_{2}}} \right)}\] done
clear
D)
\[T=2\pi \sqrt{\left( \frac{m{{K}_{1}}{{K}_{2}}}{{{K}_{1}}+{{K}_{2}}} \right)}\] done
clear
View Solution play_arrow
-
question_answer8)
A spring is stretched by 0.20 m, when a mass of 0.50 kg is suspended. When a mass of 0.25 kg is suspended, then its period of oscillation will be \[(g=10m/{{s}^{2}})\]
A)
0.328 sec done
clear
B)
0.628 sec done
clear
C)
0.137 sec done
clear
D)
1.00 sec done
clear
View Solution play_arrow
-
question_answer9)
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes simple harmonic oscillations with a time period T. If the mass is increased by m then the time period becomes \[\left( \frac{5}{4}T \right)\]. The ratio of \[T\frac{p}{p-1}\] is [CPMT 1991]
A)
9/16 done
clear
B)
25/16 done
clear
C)
4/5 done
clear
D)
5/4 done
clear
View Solution play_arrow
-
question_answer10)
A spring having a spring constant ?K? is loaded with a mass ?m?. The spring is cut into two equal parts and one of these is loaded again with the same mass. The new spring constant is [NCERT 1990; KCET 1999; Kerala PMT 2004; BCECE 2004]
A)
\[K/2\] done
clear
B)
\[K\] done
clear
C)
\[2K\] done
clear
D)
\[{{K}^{2}}\] done
clear
View Solution play_arrow
-
question_answer11)
A weightless spring which has a force constant oscillates with frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from it. The frequency of oscillation will now become [CPMT 1988]
A)
\[n\] done
clear
B)
\[m\left( g+\sqrt{\frac{{{\pi }^{2}}}{2}gh} \right)\] done
clear
C)
\[n/\sqrt{2}\] done
clear
D)
\[n{{(2)}^{1/2}}\] done
clear
View Solution play_arrow
-
question_answer12)
A mass M is suspended from a light spring. An additional mass m added displaces the spring further by a distance x. Now the combined mass will oscillate on the spring with period [CPMT 1989, 1998 ; UPSEAT 2000]
A)
\[T=2\pi \sqrt{\left( mg/x(M+m) \right)}\] done
clear
B)
\[T=2\pi \sqrt{\left( (M+m)x/mg \right)}\] done
clear
C)
\[T=(\pi /2)\sqrt{\left( mg/x(M+m) \right)}\] done
clear
D)
\[T=2\pi \sqrt{\left( (M+m)/mgx \right)}\] done
clear
View Solution play_arrow
-
question_answer13)
In the figure, \[{{S}_{1}}\] and \[{{S}_{2}}\] are identical springs. The oscillation frequency of the mass m is \[f\]. If one spring is removed, the frequency will become [CPMT 1971]
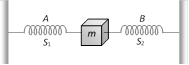
A)
\[f\] done
clear
B)
\[f\times 2\] done
clear
C)
\[f\times \sqrt{2}\] done
clear
D)
\[f/\sqrt{2}\] done
clear
View Solution play_arrow
-
question_answer14)
The vertical extension in a light spring by a weight of 1 kg suspended from the wire is 9.8 cm. The period of oscillation [CPMT 1981; MP PMT 2003]
A)
\[20\pi \sec \] done
clear
B)
\[2\pi \sec \] done
clear
C)
\[2\pi /10\sec \] done
clear
D)
\[200\pi \sec \] done
clear
View Solution play_arrow
-
question_answer15)
A particle of mass 200 gm executes S.H.M. The restoring force is provided by a spring of force constant 80 N / m. The time period of oscillations is [MP PET 1994]
A)
0.31 sec done
clear
B)
0.15 sec done
clear
C)
0.05 sec done
clear
D)
0.02 sec done
clear
View Solution play_arrow
-
question_answer16)
The length of a spring is l and its force constant is k. When a weight W is suspended from it, its length increases by x. If the spring is cut into two equal parts and put in parallel and the same weight W is suspended from them, then the extension will be [MP PMT 1994]
A)
\[2x\] done
clear
B)
\[x\] done
clear
C)
\[\frac{x}{2}\] done
clear
D)
\[\frac{x}{4}\] done
clear
View Solution play_arrow
-
question_answer17)
A block is placed on a frictionless horizontal table. The mass of the block is m and springs are attached on either side with force constants \[{{K}_{1}}\]and\[{{K}_{2}}\]. If the block is displaced a little and left to oscillate, then the angular frequency of oscillation will be [MP PMT 1994]
A)
\[{{\left( \frac{{{K}_{1}}+{{K}_{2}}}{m} \right)}^{1/2}}\] done
clear
B)
\[{{\left[ \frac{{{K}_{1}}{{K}_{2}}}{m({{K}_{1}}+{{K}_{2}})} \right]}^{1/2}}\] done
clear
C)
\[{{\left[ \frac{{{K}_{1}}{{K}_{2}}}{({{K}_{1}}-{{K}_{2}})m} \right]}^{1/2}}\] done
clear
D)
\[{{\left[ \frac{K_{1}^{2}+K_{2}^{2}}{({{K}_{1}}+{{K}_{2}})m} \right]}^{1/2}}\] done
clear
View Solution play_arrow
-
question_answer18)
A uniform spring of force constant k is cut into two pieces, the lengths of which are in the ratio 1 : 2. The ratio of the force constants of the shorter and the longer pieces is [Manipal MEE 1995]
A)
1 : 3 done
clear
B)
1 : 2 done
clear
C)
2 : 3 done
clear
D)
2 : 1 done
clear
View Solution play_arrow
-
question_answer19)
A mass m =100 gms is attached at the end of a light spring which oscillates on a frictionless horizontal table with an amplitude equal to 0.16 metre and time period equal to 2 sec. Initially the mass is released from rest at t = 0 and displacement \[x=-0.16\] metre. The expression for the displacement of the mass at any time t is [MP PMT 1995]
A)
\[x=0.16\cos (\pi t)\] done
clear
B)
\[x=-\,0.16\cos (\pi t)\] done
clear
C)
\[x=0.16\sin (\pi t+\pi )\] done
clear
D)
\[x=-\,0.16\sin (\pi t+\pi )\] done
clear
View Solution play_arrow
-
question_answer20)
A block of mass m, attached to a spring of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest, if the block moves a distance x from the mean position, then [MP PET 1996]
A)
\[a\sqrt{2}\] done
clear
B)
\[\frac{3E}{4}\] done
clear
C)
\[\frac{\sqrt{3}}{4}E\] done
clear
D)
\[\frac{E}{2}\] done
clear
View Solution play_arrow
-
question_answer21)
The force constants of two springs are \[{{K}_{1}}\] and \[{{K}_{2}}\]. Both are stretched till their elastic energies are equal. If the stretching forces are \[{{F}_{1}}\] and \[{{F}_{2}}\], then \[{{F}_{1}}:{{F}_{2}}\] is [MP PET 2002]
A)
\[{{K}_{1}}:{{K}_{2}}\] done
clear
B)
\[{{K}_{2}}:{{K}_{1}}\] done
clear
C)
\[\sqrt{{{K}_{1}}}:\sqrt{{{K}_{2}}}\] done
clear
D)
\[K_{1}^{2}:K_{2}^{2}\] done
clear
View Solution play_arrow
-
question_answer22)
A mass m is vertically suspended from a spring of negligible mass; the system oscillates with a frequency n. What will be the frequency of the system if a mass 4 m is suspended from the same spring [CBSE PMT 1998]
A)
\[n/4\] done
clear
B)
\[4n\] done
clear
C)
\[n/2\] done
clear
D)
\[2n\] done
clear
View Solution play_arrow
-
question_answer23)
If the period of oscillation of mass m suspended from a spring is 2 sec, then the period of mass 4m will be [AIIMS 1998]
A)
1 sec done
clear
B)
2 sec done
clear
C)
3 sec done
clear
D)
4 sec done
clear
View Solution play_arrow
-
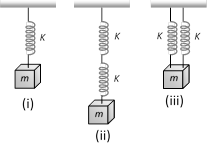
question_answer24)
Five identical springs are used in the following three configurations. The time periods of vertical oscillations in configurations (i), (ii) and (iii) are in the ratio [AMU 1995]
A)
\[1:\sqrt{2}:\frac{1}{\sqrt{2}}\] done
clear
B)
\[2:\sqrt{2}:\frac{1}{\sqrt{2}}\] done
clear
C)
\[\frac{1}{\sqrt{2}}:2:1\] done
clear
D)
\[2:\frac{1}{\sqrt{2}}:1\] done
clear
View Solution play_arrow
-
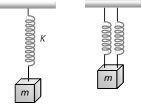
question_answer25)
A mass m performs oscillations of period T when hanged by spring of force constant K. If spring is cut in two parts and arranged in parallel and same mass is oscillated by them, then the new time period will be [CPMT 1995; RPET 1997; RPMT 2003]
A)
2T done
clear
B)
T done
clear
C)
\[\frac{T}{\sqrt{2}}\] done
clear
D)
\[\frac{T}{2}\] done
clear
View Solution play_arrow
-
question_answer26)
If a watch with a wound spring is taken on to the moon, it [AFMC 1993]
A)
Runs faster done
clear
B)
Runs slower done
clear
C)
Does not work done
clear
D)
Shows no change done
clear
View Solution play_arrow
-
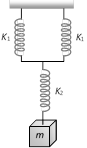
question_answer27)
What will be the force constant of the spring system shown in the figure [RPET 1996; Kerala (Med./ Engg.) 2005]
A)
\[\frac{{{K}_{1}}}{2}+{{K}_{2}}\] done
clear
B)
\[{{\left[ \frac{1}{2{{K}_{1}}}+\frac{1}{{{K}_{2}}} \right]}^{-1}}\] done
clear
C)
\[\frac{1}{2{{K}_{1}}}+\frac{1}{{{K}_{2}}}\] done
clear
D)
\[{{\left[ \frac{2}{{{K}_{1}}}+\frac{1}{{{K}_{1}}} \right]}^{-1}}\] done
clear
View Solution play_arrow
-
question_answer28)
Two springs have spring constants \[{{K}_{A}}\] and \[{{K}_{B}}\] and \[{{K}_{A}}>{{K}_{B}}\]. The work required to stretch them by same extension will be [RPMT 1999]
A)
More in spring A done
clear
B)
More in spring B done
clear
C)
Equal in both done
clear
D)
Noting can be said done
clear
View Solution play_arrow
-
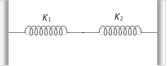
question_answer29)
The effective spring constant of two spring system as shown in figure will be [RPMT 1999]
A)
\[{{K}_{1}}+{{K}_{2}}\] done
clear
B)
\[{{K}_{1}}{{K}_{2}}/{{K}_{1}}+{{K}_{2}}\] done
clear
C)
\[{{K}_{1}}-{{K}_{2}}\] done
clear
D)
\[{{K}_{1}}{{K}_{2}}/{{K}_{1}}-{{K}_{2}}\] done
clear
View Solution play_arrow
-
question_answer30)
A mass m attached to a spring oscillates every 2 sec. If the mass is increased by 2 kg, then time-period increases by 1 sec. The initial mass is [CBSE PMT 2000; AIIMS 2000; MP PET 2000; DPMT 2001; Pb. PMT 2003]
A)
1.6 kg done
clear
B)
3.9 kg done
clear
C)
9.6 kg done
clear
D)
12.6 kg done
clear
View Solution play_arrow
-
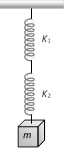
question_answer31)
A mass M is suspended by two springs of force constants K1 and K2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is [MP PMT 2000; RPET 2001]
A)
\[\frac{Mg}{{{K}_{1}}+{{K}_{2}}}\] done
clear
B)
\[\frac{Mg\,({{K}_{1}}+{{K}_{2}})}{{{K}_{1}}{{K}_{2}}}\] done
clear
C)
\[\frac{Mg\,{{K}_{1}}{{K}_{2}}}{{{K}_{1}}+{{K}_{2}}}\] done
clear
D)
\[\frac{{{K}_{1}}+{{K}_{2}}}{{{K}_{1}}{{K}_{2}}Mg}\] done
clear
View Solution play_arrow
-
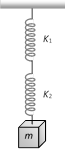
question_answer32)
The frequency of oscillation of the springs shown in the figure will be [AIIMS 2001; Pb. PET 2002]
A)
\[\frac{1}{2\pi }\sqrt{\frac{K}{m}}\] done
clear
B)
\[\frac{1}{2\pi }\sqrt{\frac{({{K}_{1}}+{{K}_{2}})m}{{{K}_{1}}{{K}_{2}}}}\] done
clear
C)
\[2\pi \sqrt{\frac{K}{m}}\] done
clear
D)
\[\frac{1}{2\pi }\sqrt{\frac{{{K}_{1}}{{K}_{2}}}{m({{K}_{1}}+{{K}_{2}})}}\] done
clear
View Solution play_arrow
-
question_answer33)
The scale of a spring balance reading from 0 to 10 kg is 0.25 m long. A body suspended from the balance oscillates vertically with a period of \[\pi /10\] second. The mass suspended is (neglect the mass of the spring) [Kerala (Engg.) 2001]
A)
10 kg done
clear
B)
0.98 kg done
clear
C)
5 kg done
clear
D)
20 kg done
clear
View Solution play_arrow
-
question_answer34)
If a spring has time period T, and is cut into n equal parts, then the time period of each part will be [AIEEE 2002]
A)
\[T\sqrt{n}\] done
clear
B)
\[T/\sqrt{n}\] done
clear
C)
nT done
clear
D)
T done
clear
View Solution play_arrow
-
question_answer35)
One-forth length of a spring of force constant K is cut away. The force constant of the remaining spring will be [MP PET 2002]
A)
\[\frac{3}{4}K\] done
clear
B)
\[\frac{4}{3}K\] done
clear
C)
K done
clear
D)
4 K done
clear
View Solution play_arrow
-
question_answer36)
A mass m is suspended separately by two different springs of spring constant K1 and K2 gives the time-period \[{{t}_{1}}\] and \[{{t}_{2}}\]respectively. If same mass m is connected by both springs as shown in figure then time-period t is given by the relation [CBSE PMT 2002]

A)
\[t={{t}_{1}}+{{t}_{2}}\] done
clear
B)
\[t=\frac{{{t}_{1}}.{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\] done
clear
C)
\[{{t}^{2}}={{t}_{1}}^{2}+{{t}_{2}}^{2}\] done
clear
D)
\[{{t}^{-2}}={{t}_{1}}^{-2}+{{t}_{2}}^{-2}\] done
clear
View Solution play_arrow
-
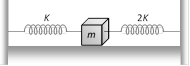
question_answer37)
Two springs of force constants K and 2K are connected to a mass as shown below. The frequency of oscillation of the mass is [RPMT 1996; DCE 2000; AIIMS 2003]
A)
\[(1/2\pi )\sqrt{(K/m)}\] done
clear
B)
\[(1/2\pi )\sqrt{(2K/m)}\] done
clear
C)
\[(1/2\pi )\sqrt{(3K/m)}\] done
clear
D)
\[(1/2\pi )\sqrt{(m/K)}\] done
clear
View Solution play_arrow
-
question_answer38)
Two springs of constant \[{{k}_{1}}\]and \[{{k}_{2}}\]are joined in series. The effective spring constant of the combination is given by [CBSE PMT 2004]
A)
\[\sqrt{{{k}_{1}}{{k}_{2}}}\] done
clear
B)
\[({{k}_{1}}+{{k}_{2}})/2\] done
clear
C)
\[{{k}_{1}}+{{k}_{2}}\] done
clear
D)
\[{{k}_{1}}{{k}_{2}}/({{k}_{1}}+{{k}_{2}})\] done
clear
View Solution play_arrow
-
question_answer39)
A particle at the end of a spring executes simple harmonic motion with a period \[{{t}_{1}}\], while the corresponding period for another spring is \[{{t}_{2}}\]. If the period of oscillation with the two springs in series is T, then [AIEEE 2004]
A)
\[T={{t}_{1}}+{{t}_{2}}\] done
clear
B)
\[{{T}^{2}}=t_{1}^{2}+t_{2}^{2}\] done
clear
C)
\[{{T}^{-1}}=t_{1}^{-1}+t_{2}^{-1}\] done
clear
D)
\[{{T}^{-2}}=t_{1}^{-2}+t_{2}^{-2}\] done
clear
View Solution play_arrow
-
question_answer40)
Infinite springs with force constant k, 2k, 4k and 8k.... respectively are connected in series. The effective force constant of the spring will be [J & K CET 2004]
A)
2K done
clear
B)
k done
clear
C)
k/2 done
clear
D)
2048 done
clear
View Solution play_arrow
-
question_answer41)
To make the frequency double of a spring oscillator, we have to [CPMT 2004; MP PMT 2005]
A)
Reduce the mass to one fourth done
clear
B)
Quardruple the mass done
clear
C)
Double of mass done
clear
D)
Half of the mass done
clear
View Solution play_arrow
-
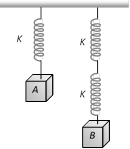
question_answer42)
The springs shown are identical. When\[A=4kg\], the elongation of spring is 1 cm. If \[B=6kg\], the elongation produced by it is [Pb. PET 2002]
A)
4 cm done
clear
B)
3 cm done
clear
C)
2 cm done
clear
D)
1 cm done
clear
View Solution play_arrow
-
question_answer43)
When a body of mass 1.0 kg is suspended from a certain light spring hanging vertically, its length increases by 5 cm. By suspending 2.0 kg block to the spring and if the block is pulled through 10 cm and released the maximum velocity in it in m/s is : (Acceleration due to gravity \[=10m/{{s}^{2}})\] [EAMCET 2003]
A)
0.5 done
clear
B)
1 done
clear
C)
2 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer44)
Two springs with spring constants \[{{K}_{1}}=1500\,N/m\] and \[{{K}_{2}}=3000\,N/m\] are stretched by the same force. The ratio of potential energy stored in spring will be [RPET 2001]
A)
2 : 1 done
clear
B)
1 : 2 done
clear
C)
4 : 1 done
clear
D)
1 : 4 done
clear
View Solution play_arrow
-
question_answer45)
If a spring extends by x on loading, then energy stored by the spring is (if T is the tension in the spring and K is the spring constant) [AFMC 2000]
A)
\[\frac{{{T}^{2}}}{2x}\] done
clear
B)
\[\frac{{{T}^{2}}}{2K}\] done
clear
C)
\[\frac{2K}{{{T}^{2}}}\] done
clear
D)
\[\frac{2{{T}^{2}}}{K}\] done
clear
View Solution play_arrow
-
question_answer46)
A weightless spring of length 60 cm and force constant 200 N/m is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is [MP PET 2003]
A)
\[\frac{\pi }{20}s\] done
clear
B)
\[\frac{\pi }{10}s\] done
clear
C)
\[\frac{\pi }{5}s\] done
clear
D)
\[\frac{\pi }{\sqrt{200}}s\] done
clear
View Solution play_arrow
-
question_answer47)
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be [MP PMT 2002; CBSE PMT 2003]
A)
T done
clear
B)
\[\frac{T}{2}\] done
clear
C)
2 T done
clear
D)
\[\frac{T}{4}\] done
clear
View Solution play_arrow
-
question_answer48)
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes S.H.M. of time period T. If the mass is increased by m, the time period becomes 5T/3. Then the ratio of m/M is [AIEEE 2003]
A)
\[\frac{5}{3}\] done
clear
B)
\[\frac{3}{5}\] done
clear
C)
\[\frac{25}{9}\] done
clear
D)
\[\frac{16}{9}\] done
clear
View Solution play_arrow
-
question_answer49)
An object is attached to the bottom of a light vertical spring and set vibrating. The maximum speed of the object is 15 cm/sec and the period is 628 milli-seconds. The amplitude of the motion in centimeters is [EAMCET 2003]
A)
3.0 done
clear
B)
2.0 done
clear
C)
1.5 done
clear
D)
1.0 done
clear
View Solution play_arrow
-
question_answer50)
When a mass m is attached to a spring, it normally extends by 0.2 m. The mass m is given a slight addition extension and released, then its time period will be [MH CET 2001]
A)
\[\frac{1}{7}\]sec done
clear
B)
1 sec done
clear
C)
\[\frac{2\pi }{7}\]sec done
clear
D)
\[\frac{2}{3\pi }\]sec done
clear
View Solution play_arrow
-
question_answer51)
If a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m, the angular frequency of the body is [CBSE PMT 2001]
A)
1.22 rad/s done
clear
B)
2.22 rad/s done
clear
C)
3.22 rad/s done
clear
D)
4.22 rad/s done
clear
View Solution play_arrow
-
question_answer52)
A mass m is suspended from a spring of length l and force constant K. The frequency of vibration of the mass is \[{{f}_{1}}\]. The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is \[{{f}_{2}}\]. Which of the following relations between the frequencies is correct [NCERT 1983; CPMT 1986; MP PMT 1991; DCE 2002]
A)
\[{{f}_{1}}=\sqrt{2}{{f}_{2}}\] done
clear
B)
\[{{f}_{1}}={{f}_{2}}\] done
clear
C)
\[{{b}^{2}}<4ac\] done
clear
D)
\[{{f}_{2}}=\sqrt{2}{{f}_{1}}\] done
clear
View Solution play_arrow
-
question_answer53)
A mass m oscillates with simple harmonic motion with frequency \[f=\frac{\omega }{2\pi }\] and amplitude A on a spring with constant K , therefore
A)
The total energy of the system is \[\frac{1}{2}K{{A}^{2}}\] done
clear
B)
The frequency is \[\frac{1}{2\pi }\sqrt{\frac{K}{M}}\] done
clear
C)
The maximum velocity occurs, when x = 0 done
clear
D)
All the above are correct done
clear
View Solution play_arrow
-
question_answer54)
Two masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is [J & K CET 2005]

A)
\[\frac{{{m}_{1}}g}{K}\] done
clear
B)
\[\frac{{{m}_{2}}g}{K}\] done
clear
C)
\[\frac{({{m}_{1}}+{{m}_{2}})g}{K}\] done
clear
D)
\[\frac{({{m}_{1}}-{{m}_{2}})g}{K}\] done
clear
View Solution play_arrow
-
question_answer55)
A spring executes SHM with mass of 10kg attached to it. The force constant of spring is 10N/m.If at any instant its velocity is 40cm/sec, the displacement will be (where amplitude is 0.5m) [RPMT 2004]
A)
0.09 m done
clear
B)
0.3 m done
clear
C)
0.03 m done
clear
D)
0.9 m done
clear
View Solution play_arrow
