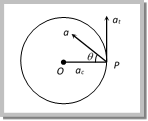
 \[\frac{\overset{\to }{\mathop{d\upsilon }}\,}{dt}=\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}\,\times \vec{r}\,+\,\vec{\omega }\,\times \,\frac{\overset{\to }{\mathop{dr}}\,}{dt}\] ?.. (ii) Here, \[\frac{\overset{\to }{\mathop{dv}}\,}{dt}=\vec{a},\,\,\] (Resultant acceleration) \[\vec{a}=\vec{\alpha }\,\times \,\vec{r}\,\,\,\,\,+\,\,\,\,\vec{\omega }\,\times \,\vec{\upsilon }\] \[\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}=\vec{\alpha }\,\,\] (Angular acceleration) \[\vec{a}=\,\,\,\,\,\,\,{{\vec{a}}_{t}}\,\,\,\,\,+\,\,\,\,\,{{\vec{a}}_{c}}\] .?. (iii) \[\frac{\overset{\to }{\mathop{dr}}\,}{dt}=\vec{\upsilon }\,\] (Linear velocity) Thus the resultant acceleration of the particle at P has two component accelerations (1) Tangential acceleration: \[\overrightarrow{{{a}_{t}}}=\overrightarrow{\alpha }\times \overrightarrow{\,r}\] It acts along the tangent to the circular path at P in the plane of circular path. According to right hand rule since \[\vec{\alpha }\] and \[\vec{r}\] are perpendicular to each other, therefore, the magnitude of tangential acceleration is given by \[|{{\overrightarrow{a}}_{t}}|\,=\,|\overrightarrow{\alpha }\,\times \,\overrightarrow{r}|\,=\,\alpha \,r\,\sin \,{{90}^{o}}\,=\alpha \,r.\] (2) Centripetal (Radial) acceleration: \[\overrightarrow{{{a}_{c}}}=\overrightarrow{\omega }\times \overrightarrow{v}\] It is also called centripetal acceleration of the particle at P. It acts along the radius of the particle at P. According to right hand rule since \[\overrightarrow{\omega }\] and \[\overrightarrow{\upsilon }\] are perpendicular to each other, therefore, the magnitude of centripetal acceleration is given by \[|{{\vec{a}}_{c}}|\,=\,|\vec{\omega }\,\times \,\vec{\upsilon }|\,=\,\omega \,\upsilon \,\sin \,{{90}^{o}}=\omega \,\upsilon \,=\,\omega (\omega \,r)\,=\,{{\omega }^{2}}r={{\upsilon }^{2}}/r\] (3) Tangential and centripetal acceleration in different motions
\[\frac{\overset{\to }{\mathop{d\upsilon }}\,}{dt}=\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}\,\times \vec{r}\,+\,\vec{\omega }\,\times \,\frac{\overset{\to }{\mathop{dr}}\,}{dt}\] ?.. (ii) Here, \[\frac{\overset{\to }{\mathop{dv}}\,}{dt}=\vec{a},\,\,\] (Resultant acceleration) \[\vec{a}=\vec{\alpha }\,\times \,\vec{r}\,\,\,\,\,+\,\,\,\,\vec{\omega }\,\times \,\vec{\upsilon }\] \[\frac{\overset{\to }{\mathop{d\omega }}\,}{dt}=\vec{\alpha }\,\,\] (Angular acceleration) \[\vec{a}=\,\,\,\,\,\,\,{{\vec{a}}_{t}}\,\,\,\,\,+\,\,\,\,\,{{\vec{a}}_{c}}\] .?. (iii) \[\frac{\overset{\to }{\mathop{dr}}\,}{dt}=\vec{\upsilon }\,\] (Linear velocity) Thus the resultant acceleration of the particle at P has two component accelerations (1) Tangential acceleration: \[\overrightarrow{{{a}_{t}}}=\overrightarrow{\alpha }\times \overrightarrow{\,r}\] It acts along the tangent to the circular path at P in the plane of circular path. According to right hand rule since \[\vec{\alpha }\] and \[\vec{r}\] are perpendicular to each other, therefore, the magnitude of tangential acceleration is given by \[|{{\overrightarrow{a}}_{t}}|\,=\,|\overrightarrow{\alpha }\,\times \,\overrightarrow{r}|\,=\,\alpha \,r\,\sin \,{{90}^{o}}\,=\alpha \,r.\] (2) Centripetal (Radial) acceleration: \[\overrightarrow{{{a}_{c}}}=\overrightarrow{\omega }\times \overrightarrow{v}\] It is also called centripetal acceleration of the particle at P. It acts along the radius of the particle at P. According to right hand rule since \[\overrightarrow{\omega }\] and \[\overrightarrow{\upsilon }\] are perpendicular to each other, therefore, the magnitude of centripetal acceleration is given by \[|{{\vec{a}}_{c}}|\,=\,|\vec{\omega }\,\times \,\vec{\upsilon }|\,=\,\omega \,\upsilon \,\sin \,{{90}^{o}}=\omega \,\upsilon \,=\,\omega (\omega \,r)\,=\,{{\omega }^{2}}r={{\upsilon }^{2}}/r\] (3) Tangential and centripetal acceleration in different motions | Centripetal acceleration | Tangential acceleration | Net acceleration | Type of motion |
| ac = 0 | at = 0 | a = 0 | Uniform translatory motion |
| ac = 0 | at ¹ 0 | a = at | Accelerated translatory motion |
| ac ¹ 0 | at = 0 | ||
| | For retarded motion | ||
| \[{{\omega }_{2}}={{\omega }_{1}}+\alpha \,t\] | \[{{\omega }_{2}}={{\omega }_{1}}-\alpha \,t\] | ||
| \[\theta ={{\omega }_{1}}t+\frac{1}{2}\alpha \,{{t}^{2}}\] | \[\theta ={{\omega }_{1}}t-\frac{1}{2}\alpha \,{{t}^{2}}\] | ||
| \[\omega _{_{2}}^{2}=\omega _{_{1}}^{2}+2\alpha \,\theta \] | \[\omega _{_{2}}^{2}=\omega _{_{1}}^{2}-2\alpha \,\theta \] | ||
| \[{{\theta }_{n}}={{\omega }_{1}}+\frac{\alpha }{2}(2n-1)\] | \[{{\theta }_{n}}={{\omega }_{1}}-\frac{\alpha }{2}(2n-1)\] |
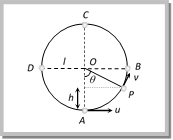 \[v=\sqrt{{{u}^{2}}-2gh}=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\] \[[As h = l l cos\,\theta = l (1 cos\,\theta )]\] where l in the length of the string (2) Tension at any point on vertical loop: Tension at general point P, According to Newton?s second law of motion. Net force towards centre = centripetal force \[T-mg\cos \theta =\frac{m{{v}^{2}}}{l}\] or \[T=mg\cos \theta +\frac{m{{v}^{2}}}{l}\] \[T=\frac{m}{l}[{{u}^{2}}-gl(2-3\cos \theta )]\] [As \[v=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\]
\[v=\sqrt{{{u}^{2}}-2gh}=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\] \[[As h = l l cos\,\theta = l (1 cos\,\theta )]\] where l in the length of the string (2) Tension at any point on vertical loop: Tension at general point P, According to Newton?s second law of motion. Net force towards centre = centripetal force \[T-mg\cos \theta =\frac{m{{v}^{2}}}{l}\] or \[T=mg\cos \theta +\frac{m{{v}^{2}}}{l}\] \[T=\frac{m}{l}[{{u}^{2}}-gl(2-3\cos \theta )]\] [As \[v=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\]  (3) Velocity and tension in a vertical loop at different positions
(3) Velocity and tension in a vertical loop at different positions | Position | Angle | Velocity | Tension |
| A | 0o | u | \[\frac{m{{u}^{2}}}{l}+mg\] |
| B | 90o | \[\sqrt{{{u}^{2}}-2gl}\] | \[\frac{m{{u}^{2}}}{l}-2mg\] |
| C | 180o | \[\sqrt{{{u}^{2}}-4gl}\] | \[\frac{m{{u}^{2}}}{l}-5mg\] |
| D | 270o | \[\sqrt{{{u}^{2}}-2gl}\] | \[\frac{m{{u}^{2}}}{l}-2mg\] |
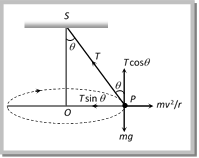 From the figure \[T\sin \theta =\frac{m{{v}^{2}}}{r}\] ?. (i) and \[T\cos \theta =mg\] ?. (ii) Tension in the string: \[T=mg\sqrt{1+{{\left( \frac{{{v}^{2}}}{rg} \right)}^{2}}}\]
From the figure \[T\sin \theta =\frac{m{{v}^{2}}}{r}\] ?. (i) and \[T\cos \theta =mg\] ?. (ii) Tension in the string: \[T=mg\sqrt{1+{{\left( \frac{{{v}^{2}}}{rg} \right)}^{2}}}\] 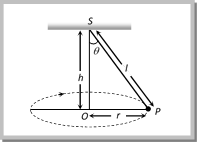 \[T=\frac{mg}{\cos \theta }=\frac{mgl}{\sqrt{{{l}^{2}}-{{r}^{2}}}}\] [As \[\cos \theta =\frac{h}{l}=\frac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l}\]] (2) Angle of string from the vertical: \[\tan \theta =\frac{{{v}^{2}}}{rg}\] (3) Linear velocity of the bob: \[v=\sqrt{gr\tan \theta }\] (4) Angular velocity of the bob: \[\omega =\sqrt{\frac{g}{r}\tan \theta }=\sqrt{\frac{g}{h}}=\sqrt{\frac{g}{l\cos \theta }}\] (5) Time period of revolution: \[{{T}_{P}}=2\pi \sqrt{\frac{l\cos \theta }{g}}=2\pi \sqrt{\frac{h}{g}}=2\pi \sqrt{\frac{{{l}^{2}}-{{r}^{2}}}{g}}=2\pi \sqrt{\frac{r}{g\tan \theta }}\] Sample problems based on conical pendulum Problem 175. A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are [AMU (Med.) 2001]
\[T=\frac{mg}{\cos \theta }=\frac{mgl}{\sqrt{{{l}^{2}}-{{r}^{2}}}}\] [As \[\cos \theta =\frac{h}{l}=\frac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l}\]] (2) Angle of string from the vertical: \[\tan \theta =\frac{{{v}^{2}}}{rg}\] (3) Linear velocity of the bob: \[v=\sqrt{gr\tan \theta }\] (4) Angular velocity of the bob: \[\omega =\sqrt{\frac{g}{r}\tan \theta }=\sqrt{\frac{g}{h}}=\sqrt{\frac{g}{l\cos \theta }}\] (5) Time period of revolution: \[{{T}_{P}}=2\pi \sqrt{\frac{l\cos \theta }{g}}=2\pi \sqrt{\frac{h}{g}}=2\pi \sqrt{\frac{{{l}^{2}}-{{r}^{2}}}{g}}=2\pi \sqrt{\frac{r}{g\tan \theta }}\] Sample problems based on conical pendulum Problem 175. A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are [AMU (Med.) 2001] 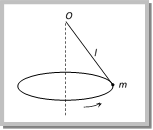 (a)
(a) 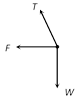 (b)
(b) 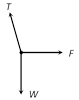 (d)
(d) 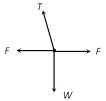 Solution: (c) Centrifugal force (F) works radially outward, Weight (w) works downward Tension (T) work along the string and towards the point of suspension Problem 176. A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/p revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is [BHU 2002]
Solution: (c) Centrifugal force (F) works radially outward, Weight (w) works downward Tension (T) work along the string and towards the point of suspension Problem 176. A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/p revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is [BHU 2002] 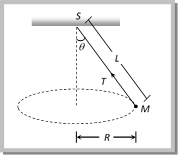 (a) ML (b) 2 ML (c) 4 ML (d) 16 ML Solution: (d) \[T\sin \theta =M{{\omega }^{2}}R\] ..... (i) \[T\,\sin \,\theta \,=\,M{{\omega }^{2}}L\sin \theta \] ..... (ii)
(a) ML (b) 2 ML (c) 4 ML (d) 16 ML Solution: (d) \[T\sin \theta =M{{\omega }^{2}}R\] ..... (i) \[T\,\sin \,\theta \,=\,M{{\omega }^{2}}L\sin \theta \] ..... (ii) 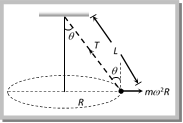 From (i) and (ii) \[T=M{{\omega }^{2}}L\]\[=M4{{\pi }^{2}}{{n}^{2}}L\] \[=M4{{\pi }^{2}}{{\left( \frac{2}{\pi } \right)}^{2}}L\]\[=16ML\] Problem 177. A string of length \[1m\] is fixed at one end and a mass of \[100gm\] is attached at the other end. The string makes \[2/\pi \] rev/sec around a vertical axis through the fixed point. The angle of inclination of the string with the vertical is (\[g=10\ m/{{\sec }^{2}}\]) (a) \[{{\tan }^{-1}}\frac{5}{8}\] (b) \[{{\tan }^{-1}}\frac{8}{5}\] (c) \[{{\cos }^{-1}}\frac{8}{5}\] (d) \[{{\cos }^{-1}}\frac{5}{8}\]
From (i) and (ii) \[T=M{{\omega }^{2}}L\]\[=M4{{\pi }^{2}}{{n}^{2}}L\] \[=M4{{\pi }^{2}}{{\left( \frac{2}{\pi } \right)}^{2}}L\]\[=16ML\] Problem 177. A string of length \[1m\] is fixed at one end and a mass of \[100gm\] is attached at the other end. The string makes \[2/\pi \] rev/sec around a vertical axis through the fixed point. The angle of inclination of the string with the vertical is (\[g=10\ m/{{\sec }^{2}}\]) (a) \[{{\tan }^{-1}}\frac{5}{8}\] (b) \[{{\tan }^{-1}}\frac{8}{5}\] (c) \[{{\cos }^{-1}}\frac{8}{5}\] (d) \[{{\cos }^{-1}}\frac{5}{8}\] 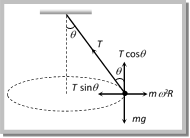 Solution: (d) For the critical condition, in equilibrium \[T\sin \theta =m\,{{\omega }^{2}}r\] and \[T\cos \theta =mg\] \[\therefore \,\,\tan \theta =\frac{{{\omega }^{2}}r}{g}\] \[\Rightarrow \,\,\frac{4{{\pi }^{2}}{{n}^{2}}r}{g}=\frac{4{{\pi }^{2}}{{(2/\pi )}^{2}}\,.\,1}{10}=\frac{8}{5}\] Sample problems (Miscellaneous) Problem 178. If the frequency of the rotating platform is f and the distance of a boy from more...
Solution: (d) For the critical condition, in equilibrium \[T\sin \theta =m\,{{\omega }^{2}}r\] and \[T\cos \theta =mg\] \[\therefore \,\,\tan \theta =\frac{{{\omega }^{2}}r}{g}\] \[\Rightarrow \,\,\frac{4{{\pi }^{2}}{{n}^{2}}r}{g}=\frac{4{{\pi }^{2}}{{(2/\pi )}^{2}}\,.\,1}{10}=\frac{8}{5}\] Sample problems (Miscellaneous) Problem 178. If the frequency of the rotating platform is f and the distance of a boy from more... | Rate law | Law of mass action | |||||||||||||
| It is an experimentally observed law. | It is a theoretical law. | |||||||||||||
| It depends on the concentration terms on which the rate of reaction actually depends | It is based upon the stoichiometry of the equation | |||||||||||||
|
Example for the reaction, \[aA+bB\to more...
Collision Theory, Energy of Activation and Arrhenius Equation
Theories of Reaction rate.
Some theories, which explain the reaction rate, are as follows:
(1) Collision theory
(i) The basic requirement for a reaction to occur is that the reacting species must collide with one another. This is the basis of collision theory for reactions.
(ii) The number of collisions that takes place per second per unit volume of the reaction mixture is known as collision frequency (Z). The value of collision frequency is very high of the order of \[{{10}^{25}}\,\text{to }{{10}^{28}}\] in case of binary collisions.
(iii) Every collision does not bring a chemical change. The collisions that actually produce the product are effective collisions. The effective collisions, which bring chemical change, are few in comparison to the total number of collisions. The collisions that do not form a product are ineffective elastic collisions, i.e., molecules just collide and disperse in different directions with different velocities.
(iv) For a collision to be effective, the following two barriers are to be cleared.
(a) Energy barrier : “The minimum amount of energy which the colliding molecules must possess as to make the chemical reaction to occur, is known as threshold energy”.
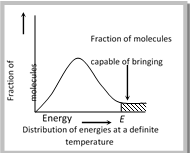
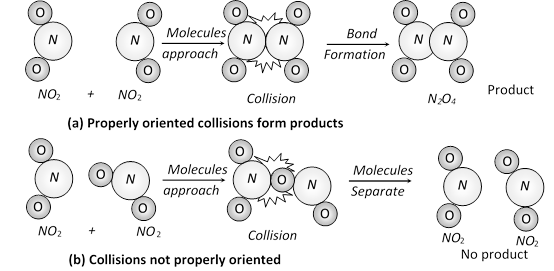 (v) Thus, the main points of collision theory are as follows,
(a) For a reaction to occur, there must be collisions between the reacting species.
(b) Only a certain fraction of the total number of collisions is effective in forming the products.
(c) For effective collisions, the molecules should possess sufficient energy as well as orientation.
(vi) The fraction of effective collisions, under ordinary conditions may vary from nearly zero to about one for ordinary reactions. Thus, the rate of reaction is proportional to :
(a) The number of collisions per unit volume per second (Collision frequency, Z) between the reacting species
(b) The fraction of effective collisions (Properly oriented and possessing sufficient energy), f
i.e., \[\text{Rate}=\frac{-dx}{dt}=f\times Z\]; Where f is fraction of effective collision and Z is the collision frequency.
(vii) The physical meaning of the activation energy is that it is the minimum relative kinetic energy which the reactant molecules must possess for changing into the products molecules during their collision. This means that the fraction of successful collision is equal to \[{{e}^{-{{E}_{a}}/RT}}\] more...
(v) Thus, the main points of collision theory are as follows,
(a) For a reaction to occur, there must be collisions between the reacting species.
(b) Only a certain fraction of the total number of collisions is effective in forming the products.
(c) For effective collisions, the molecules should possess sufficient energy as well as orientation.
(vi) The fraction of effective collisions, under ordinary conditions may vary from nearly zero to about one for ordinary reactions. Thus, the rate of reaction is proportional to :
(a) The number of collisions per unit volume per second (Collision frequency, Z) between the reacting species
(b) The fraction of effective collisions (Properly oriented and possessing sufficient energy), f
i.e., \[\text{Rate}=\frac{-dx}{dt}=f\times Z\]; Where f is fraction of effective collision and Z is the collision frequency.
(vii) The physical meaning of the activation energy is that it is the minimum relative kinetic energy which the reactant molecules must possess for changing into the products molecules during their collision. This means that the fraction of successful collision is equal to \[{{e}^{-{{E}_{a}}/RT}}\] more...
Law of Equilibrium and Equilibrium Constant
Equilibrium constant.
(1) Equilibrium constant in terms of law of mass action: The law of mass action may be applied to a reversible reaction to derive a mathematical expression for equilibrium constant known as law of chemical equilibrium.
Let us consider a simple reversible reaction, \[A+B\rightleftharpoons X+Y\] in which an equilibrium exists between the reactants (A and B) and the products (X and Y). The forward reaction is,
\[A+B\to X+Y\]
According to law of mass action,
Rate of forward reaction \[\propto [A][B]={{k}_{f}}[A][B]\]
Where \[{{k}_{f}}\] is the rate constant for the forward reaction and [A] and [B] are molar concentrations of reactants A and B respectively.
Similarly, the backward reaction is ; \[X+Y\to A+B\]
Rate of backward reaction \[\propto [X][Y]={{k}_{b}}[X][Y]\]
Where \[{{k}_{b}}\] is the rate constant for the backward reaction and [X] and [Y] are molar concentrations of products X and Y respectively.
At equilibrium, the rates of two opposing reactions become equal. Therefore, at equilibrium,
Rate of forward reaction = Rate of backward reaction
\[{{k}_{f}}[A][B]={{k}_{b}}[X][Y]\]
\[\frac{{{k}_{f}}}{{{k}_{b}}}=\frac{[X][Y]}{[A][B]}\,\,\,\,\,\text{or}\,\,\,\,\ K=\frac{[X][Y]}{[A][B]}\]
The combined constant K, which is equal to \[{{k}_{f}}/{{k}_{b}}\] is called equilibrium constant and has a constant value for a reaction at a given temperature. The above equation is known as law of chemical equilibrium.
For a general reaction of the type : \[aA+bB\rightleftharpoons cC+dD\]
The equilibrium constant may be represented as : \[K=\frac{{{[C]}^{c}}{{[D]}^{d}}}{{{[A]}^{a}}{{[B]}^{b}}}\]
where the exponents a, b, c and d have the same values as those in the balanced chemical equation. Thus, the equilibrium constant may be defined as,
“The ratio between the products of molar concentrations of the products to that of the molar concentrations of the reactants with each concentration term raised to a power equal to its stoichiometric coefficient in the balanced chemical equation at a constant temperature.”
(2) Characteristics of equilibrium constant
(i) The value of equilibrium constant is independent of the original concentration of reactants.
For example, the equilibrium constant for the reaction,
\[F{{e}^{3+}}(aq)+SC{{N}^{-}}(aq)=FeSC{{N}^{2+}}(aq)\]; \[K=\frac{[FeSC{{N}^{2+}}]}{[F{{e}^{3+}}][SC{{N}^{-}}]}=138.0\,L\,mo{{l}^{-1}}\] (at 298 K)
Whatever may be the initial concentrations of the reactants, \[F{{e}^{3+}}\] and \[SC{{N}^{-}}\] ions, the value of K comes out to be \[138.0\text{ }L\text{ }mo{{l}^{1}}\] at 298 K.
(ii) The equilibrium constant has a definite value for every reaction at a particular temperature. However, it varies with change in temperature.
For example, the equilibrium constant for the reaction between hydrogen and iodine to form hydrogen iodide is 48 at 717 K.
\[{{H}_{2}}(g)+{{I}_{2}}(g)=2HI(g)\]; \[K=\frac{{{[HI]}^{2}}}{[{{H}_{2}}][{{I}_{2}}]}=48\]
For this reaction, the value of K is fixed as long as the temperature remains constant.
(iii) For a reversible reaction, the equilibrium constant for the forward reaction is inverse of the equilibrium constant for the backward reaction.
For example, if equilibrium constant, K, for the reaction of combination between hydrogen and iodine at 717 K is 48
\[{{H}_{2}}(g)+{{I}_{2}}(g)~\rightleftharpoons 2HI\left( g \right);\] \[{K}'=\frac{{{[HI]}^{2}}}{[{{H}_{2}}][{{I}_{2}}]}=48\]
Then, the equilibrium constant for the decomposition of hydrogen iodide is the inverse of the above equilibrium constant.
\[2HI\left( g \right)\rightleftharpoons {{H}_{2}}(g)+{{I}_{2}}(g);\] more...
Kp & Kc Relationship and Characteristics of K
\[{{K}_{p}}\And {{K}_{c}}\] Relationship
Unit of equilibrium constant : Equilibrium constant K has no units i.e., dimensionless if the total number of moles of the products is exactly equal to the total number of moles of reactants. On the other hand if the number of mioles of products and reactants are not equal, K has specific units.
Units of \[{{K}_{p}}\] and \[{{K}_{c}}\] and the value of \[\Delta n\]
|