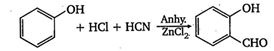question_answer 1) If E = energy, G = gravitational constant, \[I=\]impulse and \[M=\]mass, then dimensions of \[\frac{GI{{M}^{2}}}{{{E}^{2}}}\]are same as that of
A)
time
done
clear
B)
mass
done
clear
C)
length
done
clear
D)
force
done
clear
View Answer play_arrow
question_answer 2) A point initially at rest moves along \[x-\]axis. Its acceleration varies with time as \[a=(6t+5)m/{{s}^{2}}.\]If it starts from origin, the distance covered in 2 s is
A)
20 m
done
clear
B)
18 m
done
clear
C)
16 m
done
clear
D)
25 m
done
clear
View Answer play_arrow
question_answer 3)
Three blocks of masses 2 kg, 3 kg and 5 kg are connected to each other with light string and are then placed on a frictionless surface as shown in the figure. The system is pulled by a force \[F=10N,\]then tension \[{{T}_{1}}=\]
A)
1 N
done
clear
B)
5 N
done
clear
C)
8 N
done
clear
D)
10 N
done
clear
View Answer play_arrow
question_answer 4) A solid sphere rolls down two different inclined planes of same height, but of different inclinations. In both cases
A)
speed and time of descent will be same
done
clear
B)
speed will be same, but time of descent will be different
done
clear
C)
speed will be different, but time of descent will be same
done
clear
D)
speed and time of descent both are different
done
clear
View Answer play_arrow
question_answer 5) The angular amplitude of a simple pendulum is \[{{\theta }_{0}}.\]The maximum tension in its string will be
A)
\[mg(1-{{\theta }_{0}})\]
done
clear
B)
\[mg(1+{{\theta }_{0}})\]
done
clear
C)
\[mg(1-\theta _{0}^{2})\]
done
clear
D)
\[mg(1+\theta _{0}^{2})\]
done
clear
View Answer play_arrow
question_answer 6) An engine pumps up 100 kg of water through a height of 10 m in 5s. Given that the efficiency of engine is 60%. If \[g=10\,m{{s}^{-2}},\] the power of the engine is
A)
3.3 kW
done
clear
B)
0.33 kW
done
clear
C)
0.033 kW
done
clear
D)
33 kW
done
clear
View Answer play_arrow
question_answer 7) At what speed, the velocity head of water is equal to pressure head of 40 cm of Hg?
A)
10.3 m/s
done
clear
B)
2.8 m/s
done
clear
C)
5.6 m/s
done
clear
D)
8.4 m/s
done
clear
View Answer play_arrow
question_answer 8) If the electric flux entering and leaving an enclosed surface respectively are \[{{\phi }_{1}}\] and \[{{\phi }_{2}}\] the electric charge inside the surface will be
A)
\[\frac{{{\phi }_{2}}-{{\phi }_{1}}}{{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{{{\phi }_{1}}+{{\phi }_{2}}}{{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{{{\phi }_{1}}-{{\phi }_{2}}}{{{\varepsilon }_{0}}}\]
done
clear
D)
\[{{\varepsilon }_{0}}\,({{\phi }_{1}}+{{\phi }_{2}})\]
done
clear
View Answer play_arrow
question_answer 9) In the propagation of light waves, the angle between the direction of vibration and plane of polarization is
A)
\[{{0}^{o}}\]
done
clear
B)
\[{{90}^{o}}\]
done
clear
C)
\[{{45}^{o}}\]
done
clear
D)
\[{{80}^{o}}\]
done
clear
View Answer play_arrow
question_answer 10) A light emitting diode (LED) has a voltage drop of 2 V across it and passes a current of 10 mA. When it operates with a 6 V battery through a limiting resistor R, the value of R is
A)
\[40\,k\Omega \]
done
clear
B)
\[4\,k\Omega \]
done
clear
C)
\[200\,\Omega \]
done
clear
D)
\[400\,\Omega \]
done
clear
View Answer play_arrow
question_answer 11) The minimum potential difference between the base and emitter required to switch a silicon transistor ON is approximately
A)
1 V
done
clear
B)
3 V
done
clear
C)
5 V
done
clear
D)
4.2 V
done
clear
View Answer play_arrow
question_answer 12) Two stones are projected with the same speed but making different angles with the horizontal. Their horizontal ranges are equal. The angle of projection of one is \[\pi /3\]and the maximum height reached by it is 102 m. Then the maximum height reached by the other in metre is
A)
336
done
clear
B)
224
done
clear
C)
56
done
clear
D)
34
done
clear
View Answer play_arrow
question_answer 13) Which one of the following is a possible nuclear reaction?
A)
\[_{5}^{10}B+_{2}^{4}He\xrightarrow{{}}_{7}^{13}N+_{1}^{1}H\]
done
clear
B)
\[_{11}^{23}Na+_{1}^{1}H\xrightarrow{{}}_{10}^{20}Ne+_{2}^{4}He\]
done
clear
C)
\[_{93}^{239}Np+\xrightarrow{{}}_{94}^{239}Pu+{{\beta }^{-}}+\bar{v}\]
done
clear
D)
\[_{7}^{11}N+_{1}^{1}H\xrightarrow{{}}_{6}^{12}C+{{\beta }^{-}}+v\]
done
clear
View Answer play_arrow
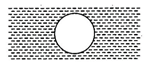
question_answer 14)
Two circular discs A and B with equal radii are blackened. They are heated to same temperature and are cooled under identical
A)
A and B have same specific heats
done
clear
B)
Specific heat of A is less
done
clear
C)
Specific heat of B is less
done
clear
D)
Nothing can be said
done
clear
View Answer play_arrow
question_answer 15) During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio \[{{C}_{p}}/{{C}_{v}}\]for the gas is
A)
4/3
done
clear
B)
2
done
clear
C)
5/3
done
clear
D)
3/2
done
clear
View Answer play_arrow
question_answer 16) The sum of two vectors \[\vec{A}\] and \[\vec{B}\] is at right angles to their difference. Then
A)
\[A=B\]
done
clear
B)
\[A=2B\]
done
clear
C)
\[B=2A\]
done
clear
D)
\[\vec{A}\] and \[\vec{B}\] have the same direction
done
clear
View Answer play_arrow
question_answer 17) A ball is thrown up at an angle with the horizontal. Then the total change of momentum by the instant it returns to ground is
A)
acceleration due to gravity \[\times \] total time of flight
done
clear
B)
weight of the ball \[\times \] half the time of flight
done
clear
C)
weight of the ball \[\times \]total time of flight
done
clear
D)
weight of the ball \[\times \]horizontal range
done
clear
View Answer play_arrow
question_answer 18) When a spring is stretched by a distance \[x,\]it exerts a force, given by \[F=(-5x-16{{x}^{3}})N\] The work done, when the spring is stretched from 0.1 m to 0.2 m is
A)
\[8.7\times {{10}^{-2}}J\]
done
clear
B)
\[12.2\times {{10}^{-2}}J\]
done
clear
C)
\[8.7\times {{10}^{-1}}J\]
done
clear
D)
\[12.2\times {{10}^{-1}}J\]
done
clear
View Answer play_arrow
question_answer 19) Time period of a simple pendulum of length\[l\] is \[{{T}_{1}}\]and time period of a uniform rod of the same length \[l\] pivoted about one end and oscillating in a vertical plane is \[{{T}_{2}}.\]Amplitude of oscillations in both the cases is small. Then\[{{T}_{1}}/{{T}_{2}}\]is
A)
\[\frac{1}{\sqrt{3}}\]
done
clear
B)
\[1\]
done
clear
C)
\[\sqrt{\frac{4}{3}}\]
done
clear
D)
\[\sqrt{\frac{3}{2}}\]
done
clear
View Answer play_arrow
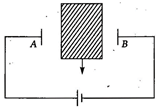
question_answer 20)
An insulator plate is passed between the plates of a capacitor. Then current
A)
first flows from A to Band then from B to A
done
clear
B)
first flows from B to A and then from A to B
done
clear
C)
always flows from B to A
done
clear
D)
always flows from A to B
done
clear
View Answer play_arrow
question_answer 21) Two parallel large thin metal sheets have equal surface charge densities \[(\sigma =26.4\times {{10}^{-12}}C/{{m}^{2}})\] of opposite signs. The electric field between these sheets is
A)
\[1.5\,N/C\]
done
clear
B)
\[1.5\times {{10}^{-10}}\,N/C\]
done
clear
C)
\[3\,N/C\]
done
clear
D)
\[3\times {{10}^{-10}}\,N/C\]
done
clear
View Answer play_arrow
question_answer 22) The electric current passes through a metallic wire produces heat because of
A)
collisions of conduction electrons with each other
done
clear
B)
collisions of the atoms of the metal with each other
done
clear
C)
the energy released in the ionization of the atoms of the metal
done
clear
D)
collisions of the conduction electrons with the atoms of the metallic wire
done
clear
View Answer play_arrow
question_answer 23) Two concentric circular coils of ten turns each are situated in the same plane. Their radii are 20 cm and 40 cm and they carry respectively 0.2 A and 0.3 A currents in opposite direction. The magnetic field in tesla at the centre is
A)
\[35\,{{\mu }_{0}}/4\]
done
clear
B)
\[\,{{\mu }_{0}}/80\]
done
clear
C)
\[7\,{{\mu }_{0}}/80\]
done
clear
D)
\[5\,{{\mu }_{0}}/4\]
done
clear
View Answer play_arrow
question_answer 24) Electromagnetic waves with frequencies greater than the critical frequency of ionosphere cannot be used for communication using sky wave propagation, because
A)
the refractive Index of the ionosphere becomes very high for \[f>{{f}_{c}}\]
done
clear
B)
the refractive index of the ionosphere becomes very low for \[f>{{f}_{c}}\]
done
clear
C)
the refractive index of the ionosphere becomes very high for \[f<{{f}_{c}}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 25) In a choke coil, the reactance \[{{X}_{L}}\]and resistance R are such that
A)
\[{{X}_{L}}=R\]
done
clear
B)
\[{{X}_{L}}>>R\]
done
clear
C)
\[{{X}_{L}}<<R\]
done
clear
D)
\[{{X}_{L}}=\infty \]
done
clear
View Answer play_arrow
question_answer 26) Reverberation time does not depend upon
A)
temperature
done
clear
B)
volume of room
done
clear
C)
size of window
done
clear
D)
carpet and curtain
done
clear
View Answer play_arrow
question_answer 27) In a potentiometer, the null point is received at 7th wire. If now we have to change the null point at 9th wire, what should we do?
A)
Attach resistance in series with battery
done
clear
B)
Increase resistance in main circuit
done
clear
C)
Decrease resistance in main circuit
done
clear
D)
Decrease applied emf
done
clear
View Answer play_arrow
question_answer 28) If average velocity becomes 4 times then what will be the effect on rms velocity at that temperature?
A)
1.4 times
done
clear
B)
4 times
done
clear
C)
2 times
done
clear
D)
\[\frac{1}{4}\] times
done
clear
View Answer play_arrow
question_answer 29) What is the Q-value of the reaction \[p+{{\,}^{7}}Li\xrightarrow{{}}{{\,}^{4}}He+{{\,}^{4}}He\] The atomic masses of \[{{\,}^{1}}H,{{\,}^{4}}He\] and \[{{\,}^{7}}Li\] are 1.007825u, 4.002603 u and 7.016004 u respectively
A)
17.35 MeV
done
clear
B)
18.06 MeV
done
clear
C)
177.35 MeV
done
clear
D)
170.35 MeV
done
clear
View Answer play_arrow
question_answer 30) A Carots engine has an efficiency of 50% at sink temperature \[50{{\,}^{o}}C.\] Calculate the temperature of source.
A)
\[133{{\,}^{o}}C\]
done
clear
B)
\[143{{\,}^{o}}C\]
done
clear
C)
\[100{{\,}^{o}}C\]
done
clear
D)
\[373{{\,}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 31) \[4{{m}^{3}}\]of water is to be pumped to a height of 20 m and forced into a reservoir at a pressure of \[2\times {{10}^{5}}N/{{m}^{2}}.\] The work done by the motor is (external pressure\[={{10}^{5}}\,N/{{m}^{2}}\])
A)
\[8\times {{10}^{5}}J\]
done
clear
B)
\[16\times {{10}^{5}}\,J\]
done
clear
C)
\[12\times {{10}^{5}}\,J\]
done
clear
D)
\[32\times {{10}^{5}}\,J\]
done
clear
View Answer play_arrow
question_answer 32) Moment of inertia of ring about its diameter is \[I.\] Then, moment of inertia about an axis passing through centre perpendicular to its plane is
A)
\[2I\]
done
clear
B)
\[\frac{I}{2}\]
done
clear
C)
\[\frac{3}{2}I\]
done
clear
D)
\[I\]
done
clear
View Answer play_arrow
question_answer 33) When both the listener and source are moving towards each other, then which of the following is true regarding frequency and wavelength of wave observed by the observer?
A)
More frequency, less wavelength
done
clear
B)
More frequency, more wavelength
done
clear
C)
Less frequency, less wavelength
done
clear
D)
More frequency, constant wavelength
done
clear
View Answer play_arrow
question_answer 34) The coefficient of friction between the tyres and the road is 0.25. The maximum speed with which car can be driven round a curve of radius 40 m without skidding is (assume\[g=10\,m{{s}^{-2}}\])
A)
\[40\,m{{s}^{-1}}\]
done
clear
B)
\[20\,m{{s}^{-1}}\]
done
clear
C)
\[15\,m{{s}^{-1}}\]
done
clear
D)
\[10\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 35) A bomb of mass 3.0 kg explodes in air into two pieces of masses 2.0 kg and 1.0 kg. The smaller mass goes at a speed of 80 m/s. The total energy-.imparted, to the two fragments is
A)
1.07 kJ
done
clear
B)
2.14 kJ
done
clear
C)
2.4 kJ
done
clear
D)
4.8 kJ
done
clear
View Answer play_arrow
question_answer 36) If distance between earth and sun become four times, then time period becomes
A)
4 times
done
clear
B)
8 times
done
clear
C)
1/4 times
done
clear
D)
1/8 times
done
clear
View Answer play_arrow
question_answer 37)
An air bubble is contained inside water. It behaves as a
A)
concave lens
done
clear
B)
convex lens
done
clear
C)
Neither convex nor concave
done
clear
D)
Cannot say
done
clear
View Answer play_arrow
question_answer 38) The power dissipated across resistance R which is connected across a battery of potential V is P. If resistance is doubled, then the power becomes
A)
1/2
done
clear
B)
2
done
clear
C)
1/4
done
clear
D)
4
done
clear
View Answer play_arrow
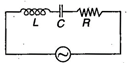
question_answer 39)
A 100 V, AC source of frequency 500 Hz is connected to an LCR circuit with\[L=8.1\,mH,\]\[C=12.5\mu F,R=10\,\Omega \]all connected in series as shown in figure. What is the quality factor of circuit?
A)
\[2.02\]
done
clear
B)
\[2.5434\]
done
clear
C)
\[20.54\]
done
clear
D)
\[200.54\]
done
clear
View Answer play_arrow
question_answer 40) The inductance of a coil is \[L=10\,H\]and resistance \[R=5\,\Omega .\]If applied voltage of battery is 10 V and it switches off in 1 millisecond, find induced emf of inductor,
A)
\[2\times {{10}^{4}}V\]
done
clear
B)
\[1.2\times {{10}^{4}}V\]
done
clear
C)
\[2\times {{10}^{-4}}V\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 41) A proton is moving in a uniform magnetic field in a circular path of radius a in a direction perpendicular to z-axis along which field B exists. Calculate the angular momentum, if the radius is a charge on proton is e.
A)
\[\frac{Be}{{{a}^{2}}}\]
done
clear
B)
\[e{{B}^{2}}a\]
done
clear
C)
\[{{a}^{2}}eB\]
done
clear
D)
\[aeB\]
done
clear
View Answer play_arrow
question_answer 42) We wish to see inside an atom. Assuming the atom to have a diameter of 100 pm, this means that one must be able to resolve a width of say 10 pm. If an electron microscope is used, the minimum electron energy required is about
A)
1.5 keV
done
clear
B)
15 keV
done
clear
C)
150 keV
done
clear
D)
1.5 MeV
done
clear
View Answer play_arrow
question_answer 43) A body from height h is dropped. If the coefficient of restitution is e, then calculate the height achieved after one bounce.
A)
\[{{h}_{1}}={{e}^{2}}h\]
done
clear
B)
\[{{h}_{1}}={{e}^{4}}h\]
done
clear
C)
\[{{h}_{1}}=eh\]
done
clear
D)
\[{{h}_{1}}=\frac{h}{e}\]
done
clear
View Answer play_arrow
question_answer 44) A beam of light travelling along \[x-\]axis is described by the electric field\[{{E}_{y}}=(600\,V{{m}^{-1}})\sin \omega (t-x/c)\] then maximum magnetic force on a charge \[q=2e,\]moving along \[y-\]axis with a speed of \[3.0\times {{10}^{7}}\,m{{s}^{-1}}\] is \[(e=1.6\times {{10}^{-19}}C)\]
A)
\[19.2\times {{10}^{-17}}N\]
done
clear
B)
\[1.92\times {{10}^{-17}}\,N\]
done
clear
C)
\[0.192\,N\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 45) Equipotential surfaces associated with an electric field which is increasing in magnitude along the \[x-\]direction are
A)
planes parallel to \[yz-\]plane
done
clear
B)
planes parallel to \[xy-\]plane
done
clear
C)
planes parallel to \[xz-\]plane
done
clear
D)
coaxial cylinders of increasing radii around the \[x-\]axis
done
clear
View Answer play_arrow
question_answer 46) If 200 MeV energy is released in the fission of a single nucleus of \[{{\,}_{92}}U{{\,}^{235}},\] how many fissions must occur per second to produce a power 1 kW?
A)
\[3.12\times {{10}^{13}}\]
done
clear
B)
\[3.12\times {{10}^{3}}\]
done
clear
C)
\[3.1\times {{10}^{17}}\]
done
clear
D)
\[3.12\times {{10}^{19}}\]
done
clear
View Answer play_arrow
question_answer 47) Find ratio of acceleration due to gravity g depth d and at height h, where d = 2h.
A)
\[1:1\]
done
clear
B)
\[1:2\]
done
clear
C)
\[2:1\]
done
clear
D)
\[1:4\]
done
clear
View Answer play_arrow
question_answer 48) A convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of combination is
A)
\[-1.5\,D\]
done
clear
B)
\[-6.5\,D\]
done
clear
C)
\[+6.5D\]
done
clear
D)
\[+\,6.67D\]
done
clear
View Answer play_arrow
question_answer 49) In a Youngs experiment, two coherent sources are placed 0.90 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1 mm from the central fringe, the wavelength monochromatic light used would be
A)
\[60\times {{10}^{-4}}cm\]
done
clear
B)
\[10\times {{10}^{-4}}cm\]
done
clear
C)
\[10\times {{10}^{-5}}cm\]
done
clear
D)
\[6\times {{10}^{-5}}cm\]
done
clear
View Answer play_arrow
question_answer 50) A bar magnet when placed at an angle of \[{{30}^{o}}\] the direction of magnetic field induction of \[5\times {{10}^{-2}}T,\]experiences a moment of couple \[25\times {{10}^{-6}}\,N-m.\] If the length of the magnet is 5 cm its pole strength is
A)
\[2\times {{10}^{-2}}A-m\]
done
clear
B)
\[5\times {{10}^{-2}}A-m\]
done
clear
C)
\[2\,A-m\]
done
clear
D)
\[5\,A-m\]
done
clear
View Answer play_arrow
question_answer 51) The number of moles of \[\text{KMn}{{\text{O}}_{\text{4}}}\]reduced by one mole of KI in alkaline medium is
A)
1
done
clear
B)
5
done
clear
C)
1/2
done
clear
D)
1/5
done
clear
View Answer play_arrow
question_answer 52) Value of \[x\] in potash alum, \[{{K}_{2}}S{{O}_{4}}.A{{l}_{x}}{{(S{{O}_{4}})}_{3}}.24{{H}_{2}}O\]
A)
4
done
clear
B)
1
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 53) Ozone is used for purifying water because
A)
it dissociates and release oxygen
done
clear
B)
do not leave any foul smell like chlorine
done
clear
C)
kills bacteria, cyst, fungi and acts as a biocide
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 54) Internal energy is sum of
A)
kinetic energy and potential energy
done
clear
B)
all types of energy of the system
done
clear
C)
energy of internal system
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 55) Total volume of atoms present in a face centred cubic unit cell of a metal is (\[r=\]atomic radius)
A)
\[\frac{20}{3}\pi {{r}^{3}}\]
done
clear
B)
\[\frac{24}{3}\pi {{r}^{3}}\]
done
clear
C)
\[\frac{12}{3}\pi {{r}^{3}}\]
done
clear
D)
\[\frac{16}{3}\pi {{r}^{3}}\]
done
clear
View Answer play_arrow
question_answer 56) If two molecules of A and B having mass 100 kg and 64 kg and rate of diffusion of A is \[12\times {{10}^{-3}},\] then what will be the rate of diffusion of B?
A)
\[15\times {{10}^{-3}}\]
done
clear
B)
\[64\times {{10}^{-3}}\]
done
clear
C)
\[~5\times {{10}^{-3}}\]
done
clear
D)
\[~46\times {{10}^{-3}}\]
done
clear
View Answer play_arrow
question_answer 57) Aniline is prepared in presence of Fe/HCl from
A)
benzene
done
clear
B)
nitrobenzene
done
clear
C)
dinitrobenzene
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 58) Difference between S and \[{{S}^{2-}}\]as \[{{S}^{2-}}\]has
A)
larger radii and larger size
done
clear
B)
smaller radii and larger size
done
clear
C)
larger radii and smaller size
done
clear
D)
smaller radii and smaller size
done
clear
View Answer play_arrow
question_answer 59) Which of the following is not correct?
A)
\[{{t}_{1/2}}=\frac{0.693}{k}\]
done
clear
B)
\[N={{N}_{0}}{{e}^{-kt}}\]
done
clear
C)
\[\frac{1}{N}=\frac{1}{{{N}_{0}}}=\ln \,k{{t}_{1/2}}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 60) Which is not in accordance to aufbau principle?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
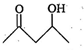
question_answer 61) \[C{{H}_{3}}C{{H}_{2}}Cl\]undergoes homolytic fission, produces
A)
\[C{{H}_{3}}\overset{\centerdot }{\mathop{C}}\,{{H}_{2}}\]and \[\overset{\centerdot }{\mathop{C}}\,l\]
done
clear
B)
\[C{{H}_{3}}\overset{\oplus }{\mathop{C}}\,{{H}_{2}}\]and \[C{{l}^{\text{o}-}}\]
done
clear
C)
\[C{{H}_{3}}\overset{\oplus }{\mathop{C}}\,{{H}_{2}}\]and \[\overset{\centerdot }{\mathop{C}}\,l\]
done
clear
D)
\[C{{H}_{3}}\overset{\centerdot }{\mathop{C}}\,{{H}_{2}}\]and \[C{{l}^{\text{o}-}}\]
done
clear
View Answer play_arrow
question_answer 62) \[C-C\]bond order in benzene is
A)
1
done
clear
B)
2
done
clear
C)
between 1 and 2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 63) In colloid particles, range of diameter is
A)
1 to 100 nm
done
clear
B)
1 to 1000 cm
done
clear
C)
1 to 1000 mm
done
clear
D)
1 to 100 km
done
clear
View Answer play_arrow
question_answer 64) \[Z{{n}^{2+}}\xrightarrow{{}}Zn(s);{{E}^{o}}=-0.76\,V\] \[C{{u}^{2+}}\xrightarrow{{}}Cu(s);{{E}^{o}}=-0.34\,V\] Which of the following is spontaneous?
A)
\[Z{{n}^{2+}}+Cu\xrightarrow{{}}Zn+C{{u}^{2+}}\]
done
clear
B)
\[C{{u}^{2+}}+Zn\xrightarrow{{}}Cu+Z{{n}^{2+}}\]
done
clear
C)
\[Z{{n}^{2+}}+C{{u}^{2+}}\xrightarrow{{}}Zn+Cu\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 65) Highest electron affinity among the following is
A)
fluorine
done
clear
B)
chlorine
done
clear
C)
sulphur
done
clear
D)
xenon
done
clear
View Answer play_arrow
question_answer 66) Which of the following noble gases is most reactive?
A)
He
done
clear
B)
Ne
done
clear
C)
Ar
done
clear
D)
Xe
done
clear
View Answer play_arrow
question_answer 67) Which one of the following is a correct set with respect to molecule, hybridisation and shape?
A)
\[BeC{{l}_{2}},\text{ }s{{p}^{2}},\,\]linear
done
clear
B)
\[BeC{{l}_{2}},\text{ }s{{p}^{2}},\]triangular planar
done
clear
C)
\[~BC{{l}_{3}},\text{ }s{{p}^{2}},\] triangular planar
done
clear
D)
\[BC{{l}_{3}},s{{p}^{3}},\]tetrahedral
done
clear
View Answer play_arrow
question_answer 68) \[{{H}_{2}}S\]is not a/an
A)
reducing agent
done
clear
B)
acidic
done
clear
C)
oxidizing agent
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 69) On doubling p and V with constant temperature, the equilibrium constant will
A)
remain constant
done
clear
B)
become double
done
clear
C)
become one-fourth
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 70) What is the electronic configuration of\[M{{n}^{2+}}\]?
A)
\[~[Ne]\text{ }3{{d}^{5}},\text{ }4{{s}^{o}}\]
done
clear
B)
\[\text{ }\!\![\!\!\text{ }Ar\text{ }\!\!]\!\!\text{ }3{{d}^{5}},\text{ }4{{s}^{2}}\]
done
clear
C)
\[\text{ }\!\![\!\!\text{ }Ar\text{ }\!\!]\!\!\text{ }3{{d}^{5}},\text{ }4{{s}^{0}}\]
done
clear
D)
\[\text{ }\!\![\!\!\text{ }Ne\text{ }\!\!]\!\!\text{ }3{{d}^{5}},\text{ }4{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 71) Increase in atomic size down the group is due to
A)
increase in number of electrons
done
clear
B)
increase in number of protons and neutrons
done
clear
C)
increase in number of protons
done
clear
D)
increase in number of protons, neutrons and electrons
done
clear
View Answer play_arrow
question_answer 72) Which is tribasic acid?
A)
\[{{H}_{3}}P{{O}_{2}}\]
done
clear
B)
\[{{H}_{3}}P{{O}_{4}}\]
done
clear
C)
\[{{H}_{4}}{{P}_{2}}{{O}_{7}}\]
done
clear
D)
\[{{H}_{3}}P{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 73) Highest ionizing power is exhibited by
A)
\[\alpha -\] rays
done
clear
B)
\[\beta -\]rays
done
clear
C)
\[\gamma -\]rays
done
clear
D)
\[X-\]rays
done
clear
View Answer play_arrow
question_answer 74) Blister copper is
A)
impure \[Cu\]
done
clear
B)
\[Cu\]alloy
done
clear
C)
pure \[Cu\]
done
clear
D)
Cu having 1% impurity
done
clear
View Answer play_arrow
question_answer 75) Claisen condensation is not given by
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 76) \[AgN{{O}_{3}}\]does not give precipitate with \[CHC{{l}_{3}}\] because
A)
\[CHC{{l}_{3}}\] does not ionize in water
done
clear
B)
\[Agn{{O}_{3}}\] is chemically inert
done
clear
C)
\[CHC{{l}_{3}}\] is chemically inert
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 77) \[_{90}T{{h}^{228}}\xrightarrow{{}}{{\,}_{83}}B{{i}^{212}}\]by
A)
\[4\alpha ,1\beta \]
done
clear
B)
\[4\alpha ,2\beta ,\]
done
clear
C)
\[5\alpha ,1\beta \]
done
clear
D)
\[5\alpha ,2\beta ,\]
done
clear
View Answer play_arrow
question_answer 78) Blood cells do not shrink in blood because blood is
A)
hypotonic
done
clear
B)
isotonic
done
clear
C)
equimolar
done
clear
D)
hypeitonic
done
clear
View Answer play_arrow
question_answer 79) The compound in which underlined carbon uses only its \[s{{p}^{3}}\]hybrid orbitals for bond formation is
A)
\[C{{H}_{3}}\underset{\scriptscriptstyle-}{C}OOH\]
done
clear
B)
\[C{{H}_{3}}\underline{C}ON{{H}_{2}}\]
done
clear
C)
\[C{{H}_{3}}\underline{C}{{H}_{2}}OH\]
done
clear
D)
\[C{{H}_{3}}\underline{C}H=C{{H}_{2}}\]
done
clear
View Answer play_arrow
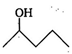
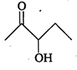
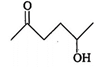
question_answer 80) t-butyl alcohol is
A)
2-methyl propan-2-ol
done
clear
B)
2-methyl propan-1-ol
done
clear
C)
3-methyl butan-1-ol
done
clear
D)
3-methyl butan-2-ol
done
clear
View Answer play_arrow
question_answer 81) Optical isomerism is shown by
A)
propanol-2
done
clear
B)
butanol-2
done
clear
C)
ethanol
done
clear
D)
methanol
done
clear
View Answer play_arrow
question_answer 82) When \[{{C}_{2}}{{H}_{2}},C{{H}_{4}}\]and \[{{C}_{2}}{{H}_{4}}\]passes through a test tube which have ammoniacal \[C{{u}_{2}}C{{l}_{2}},\]find out which gas comes out unaffected from test tube?
A)
\[{{C}_{2}}{{H}_{2}}\]and \[C{{H}_{4}}\]
done
clear
B)
\[{{C}_{2}}{{H}_{2}}\]and \[{{C}_{2}}{{H}_{4}}\]
done
clear
C)
\[{{C}_{2}}{{H}_{4}}\]and \[C{{H}_{4}}\]
done
clear
D)
\[{{C}_{2}}{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 83) When hydrogen molecules decomposed into its atoms which conditions gives maximum yield of H atoms?
A)
High temperature and low pressure
done
clear
B)
Low temperature and high pressure
done
clear
C)
High temperature and high pressure
done
clear
D)
Low temperature and low pressure
done
clear
View Answer play_arrow
question_answer 84) Natural rubber is a polymer of
A)
styrene
done
clear
B)
chloroprene
done
clear
C)
\[C{{H}_{2}}=\underset{C{{H}_{3}}}{\mathop{\underset{|}{\mathop{C}}\,}}\,-CH=C{{H}_{2}}\]or isoprene
done
clear
D)
1, 3-butadiene
done
clear
View Answer play_arrow
question_answer 85) Which of the following compounds is aromatic?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 86) The value of \[\Lambda _{eq}^{\infty }\] for\[N{{H}_{4}}Cl,NaOH\] and\[NaCl\] are respectively, 149.74, 248.1 and \[126.4\,oh{{m}^{-1}}\,c{{m}^{2}}e{{q}^{-1}}.\] The value of \[A_{eq}^{\infty }\]of \[N{{H}_{4}}OH\]is
A)
371.44
done
clear
B)
271.44
done
clear
C)
71.44
done
clear
D)
Cannot be predicted from given data
done
clear
View Answer play_arrow
question_answer 87) Number of atoms of He in 100 u of He (atomic wt of He is 4) are
A)
25
done
clear
B)
100
done
clear
C)
50
done
clear
D)
\[100\times 6\times {{10}^{-23}}\]
done
clear
View Answer play_arrow
question_answer 88) Which has least gold number?
A)
Gelatin
done
clear
B)
Starch
done
clear
C)
Albumin
done
clear
D)
Blood
done
clear
View Answer play_arrow
question_answer 89) In a compound C, H and N are present in 9 : 1 : 3.5 by weight. If molecular weight of the compound is 108, then the molecular formula of the compound is
A)
\[{{C}_{2}}{{H}_{6}}{{N}_{2}}\]
done
clear
B)
\[{{C}_{3}}{{H}_{4}}N\]
done
clear
C)
\[{{C}_{6}}{{H}_{8}}{{N}_{2}}\]
done
clear
D)
\[{{C}_{9}}{{H}_{12}}{{N}_{3}}\]
done
clear
View Answer play_arrow
question_answer 90) In the following reaction \[{{C}_{2}}{{H}_{2}}\xrightarrow[HgS{{O}_{4}}/{{H}_{2}}S{{O}_{4}}]{{{H}_{2}}O}X\rightleftharpoons C{{H}_{3}}CHO,\]What is \[X\]?
A)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
B)
\[C{{H}_{3}}-O-C{{H}_{3}}\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}CHO\]
done
clear
D)
\[C{{H}_{2}}=CHOH\]
done
clear
View Answer play_arrow
question_answer 91) Which one of the following will most readily be dehydrated in acidic conditions?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 92) Which of the following solutions will have \[pH=9\]at 298 K?
A)
\[1\times {{10}^{-9}}\,M\,HCl\]solution
done
clear
B)
\[1\times {{10}^{-5}}\,M\,NaOH\]solution
done
clear
C)
\[1\times {{10}^{-9}}\,M\,KOH\]solution
done
clear
D)
Both (a) and (b)
done
clear
View Answer play_arrow
question_answer 93)
The following data are for the decomposition of ammonium nitrite in aqueous solution. Vol. of \[{{N}_{2}}\]in cc Times (min) 6.25 10 9.00 15 11.40 20 13.65 25 35.65 Infinity
The order of reaction is
A)
zero
done
clear
B)
one
done
clear
C)
two
done
clear
D)
three
done
clear
View Answer play_arrow
question_answer 94) An alkyl halide by formation of its Grignard reagent and heating with water yields propane. What is the original alkyl halide?
A)
Methyl iodide
done
clear
B)
Ethyl iodide
done
clear
C)
Ethyl bromide
done
clear
D)
Propyl bromide
done
clear
View Answer play_arrow
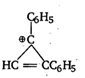
question_answer 95)
The following reaction is known as
A)
Perkin reaction
done
clear
B)
Gattermann reaction
done
clear
C)
Kolbe reaction
done
clear
D)
Gattermann-aldehyde reaction
done
clear
View Answer play_arrow
question_answer 96) Aldehyde with \[N{{H}_{2}}.N{{H}_{2}}\]forms
A)
hydrazones
done
clear
B)
aniline
done
clear
C)
nitrobenzene
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 97) Van t Hoff factor of \[Ca{{(N{{O}_{3}})}_{2}}\]us
A)
one
done
clear
B)
two
done
clear
C)
three
done
clear
D)
four
done
clear
View Answer play_arrow
question_answer 98) 1 mole of \[{{H}_{2}}\]and 2 moles of \[{{I}_{2}}\]are taken initially in a two litre vessel. The number of moles of \[{{H}_{2}}\]at equilibrium is 0.2. Then, the number of moles of \[{{I}_{2}}\]and HI at equilibrium are
A)
1.2, 1.6
done
clear
B)
1.8, 1.0
done
clear
C)
0.4, 2.4
done
clear
D)
0.8, 2.0
done
clear
View Answer play_arrow
question_answer 99) The volume of water to be added to 100 cm3 of \[0.5\text{ }N\text{ }{{H}_{2}}S{{O}_{4}}\]to get decinormal concentration is
A)
\[400\,c{{m}^{3}}\]
done
clear
B)
\[450\,c{{m}^{3}}\]
done
clear
C)
\[~500\,c{{m}^{3}}\]
done
clear
D)
\[100\,c{{m}^{3}}\]
done
clear
View Answer play_arrow
question_answer 100) 1.520 g of hydroxide of a metal on ignition gave 0.995 g of oxide. The equivalent weight of metal is
A)
1.52
done
clear
B)
0.995
done
clear
C)
190
done
clear
D)
9
done
clear
View Answer play_arrow
question_answer 101) If \[f:R\to R\]is defined by \[f(x)=[2x]-2[x]\] for all \[x\in R,\]where \[[x]\]is the greatest integer not exceeding x, then the range of\[f\]is
A)
\[\{x\in R:0\le x\le 1\}\]
done
clear
B)
\[(0,1)\]
done
clear
C)
\[\{x\in R:x>0\}\]
done
clear
D)
\[\{x\in R:x\le 0\}\]
done
clear
View Answer play_arrow
question_answer 102) If \[x=\sqrt{\frac{2+\sqrt{3}}{2-\sqrt{3}},}\]then \[{{x}^{2}}{{(x-4)}^{2}}\] is equal to
A)
7
done
clear
B)
4
done
clear
C)
2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 103) For all integers \[n\ge 1,\]which of the following is divisible by 9?
A)
\[{{8}^{n}}+1\]
done
clear
B)
\[{{4}^{n}}-3n-1\]
done
clear
C)
\[{{3}^{2n}}+3n+1\]
done
clear
D)
\[{{10}^{n}}+1\]
done
clear
View Answer play_arrow
question_answer 104) Eight different letters of an alphabet are given Words of four letters from these are formed The number of such words with at least one letter repeated is
A)
\[\left( _{4}^{8} \right)-{{\,}^{8}}{{P}_{4}}\]
done
clear
B)
\[{{8}^{4}}+\left( _{4}^{8} \right)\]
done
clear
C)
\[{{8}^{4}}-{{\,}^{8}}{{P}_{4}}\]
done
clear
D)
\[{{8}^{4}}-\left( _{4}^{8} \right)\]
done
clear
View Answer play_arrow
question_answer 105) The number of natural numbers less than 1000, in which no two digits are repeated is
A)
738
done
clear
B)
792
done
clear
C)
837
done
clear
D)
720
done
clear
View Answer play_arrow
question_answer 106) \[1+\frac{2}{4}+\frac{2.5}{4.8}+\frac{2.5.8}{4.8.12}+\frac{2.5.8.11}{4.8.12.16}+...\]is equal to
A)
\[{{4}^{-2/3}}\]
done
clear
B)
\[\sqrt[3]{16}\]
done
clear
C)
\[\sqrt[3]{4}\]
done
clear
D)
\[{{4}^{3/2}}\]
done
clear
View Answer play_arrow
question_answer 107) The coefficient of \[{{x}^{n}}\]in\[\frac{1-2x}{{{e}^{x}}}\]is
A)
\[\frac{(1+2n)}{n!}\]
done
clear
B)
\[{{(-1)}^{n}}.\frac{\left( 1+2n \right)}{n!}\]
done
clear
C)
\[{{(-1)}^{n}}.\frac{(1-2n)}{n!}\]
done
clear
D)
\[{{(-1)}^{n}}.\frac{(1+4n)}{n!}\]
done
clear
View Answer play_arrow
question_answer 108) If \[\sqrt{9{{x}^{2}}+6x+1}<(2-x),\]then
A)
\[x\in \left( -\frac{3}{2},\frac{1}{4} \right)\]
done
clear
B)
\[x\in \left( -\frac{3}{2},\frac{1}{4} \right]\]
done
clear
C)
\[x\in \left[ -\frac{3}{2},\frac{1}{4} \right)\]
done
clear
D)
\[x<\frac{1}{4}\]
done
clear
View Answer play_arrow
question_answer 109) The difference between two roots of the equation \[{{x}^{3}}-13{{x}^{2}}+15x+189=0\] is\[2.\]Then, the roots of the equation are
A)
\[-3,5,7\]
done
clear
B)
\[-3,-7,-9\]
done
clear
C)
\[3,-5,7\]
done
clear
D)
\[-3,7,9\]
done
clear
View Answer play_arrow
question_answer 110) If \[\alpha ,\beta ,\gamma \]are the roots of the equation \[{{x}^{3}}-6{{x}^{2}}+11x+6=0,\]then \[\sum {{\alpha }^{2}}\beta +\sum {{\alpha }^{2}}\beta +\sum \alpha {{\beta }^{2}}\]is equal to
A)
80
done
clear
B)
84
done
clear
C)
90
done
clear
D)
- 84
done
clear
View Answer play_arrow
question_answer 111) If A is an inverrible matrix of order n, then the determinant of \[adj\,(A)\] is equal to
A)
\[|A{{|}^{n}}\]
done
clear
B)
\[|A{{|}^{n+1}}\]
done
clear
C)
\[|A{{|}^{n-1}}\]
done
clear
D)
\[|A{{|}^{n+2}}\]
done
clear
View Answer play_arrow
question_answer 112) \[\left| \begin{matrix} \log e & \log {{e}^{2}} & \log {{e}^{3}} \\ \log {{e}^{2}} & \log {{e}^{3}} & \log {{e}^{4}} \\ \log {{e}^{3}} & \log {{e}^{4}} & \log {{e}^{5}} \\ \end{matrix} \right|\]is equal to
A)
0
done
clear
B)
1
done
clear
C)
4 loge
done
clear
D)
5 loge
done
clear
View Answer play_arrow
question_answer 113) The equation of the locus of \[z\] such that \[\left| \frac{z-i}{z+i} \right|=2,\]where \[z=x+iy\]is a complex number, is
A)
\[3{{x}^{2}}+\text{ }3{{y}^{2}}+10y\text{ }-3=0\]
done
clear
B)
\[~3{{x}^{2}}+3{{y}^{2}}+10y+3=0\]
done
clear
C)
\[3{{x}^{2}}-3{{y}^{2}}-10y-3=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-5y+3=0\]
done
clear
View Answer play_arrow
question_answer 114) If \[5\cos x+12\cos y=13,\] then the maximum value of \[5\,\sin x+12\sin y\]is
A)
12
done
clear
B)
\[\sqrt{120}\]
done
clear
C)
\[\sqrt{20}\]
done
clear
D)
13
done
clear
View Answer play_arrow
question_answer 115) The quadratic equation whose roots are \[{{\sin }^{2}}{{18}^{o}}\]and \[{{\cos }^{2}}{{36}^{o}}\]is
A)
\[~16{{x}^{2}}-12x+1=0\]
done
clear
B)
\[16{{x}^{2}}+12x+1=0\]
done
clear
C)
\[16{{x}^{2}}-12x-1=0\]
done
clear
D)
\[16{{x}^{2}}+\text{10}x+1=0\]
done
clear
View Answer play_arrow
question_answer 116) For all values of \[\theta ,\] the values of \[3-\cos \theta +\cos \left( \theta +\frac{\pi }{3} \right)\] lie in the interval
A)
\[[-2,3]\]
done
clear
B)
\[[-2,1]\]
done
clear
C)
\[[2,4]\]
done
clear
D)
\[[1,5]\]
done
clear
View Answer play_arrow
question_answer 117) If \[x=\tan {{15}^{o}},y=\cos ec{{75}^{o}}\]and \[z=4\sin {{18}^{o}},\]then
A)
\[x<y<z\]
done
clear
B)
\[y<z<x\]
done
clear
C)
\[z<x<\text{ }y\]
done
clear
D)
\[~x<z<\text{ }y\]
done
clear
View Answer play_arrow
question_answer 118) If in \[\Delta \,ABC,\,\,\tan \frac{A}{2}=\frac{5}{6}\] and \[\tan \frac{C}{2}=\frac{2}{5},\]then\[a,b,c\] are such that
A)
\[{{b}^{2}}=ac\]
done
clear
B)
\[2b=a+c\]
done
clear
C)
\[2ac=b(a+c)\]
done
clear
D)
\[a+b=c\]
done
clear
View Answer play_arrow
question_answer 119) If \[b+c=3a,\]then \[\cot \frac{B}{2}\cot \frac{C}{2}\]is equal to
A)
3
done
clear
B)
1
done
clear
C)
4
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 120) The elevation of an object on a hill is observed from a certain point in the horizontal plane through its base, to be \[{{30}^{o}}.\] After walking 120 m towards it on level ground the elevation is found to be \[{{60}^{o}}.\] Then the height of the object (in metres) is
A)
120
done
clear
B)
\[60\sqrt{3}\]
done
clear
C)
\[120\sqrt{3}\]
done
clear
D)
\[60\]
done
clear
View Answer play_arrow
question_answer 121) If \[\vec{a}+\vec{b}+\vec{c}=\vec{o}\]and \[|\vec{a}|=3,|\vec{b}|=4\]and \[|\vec{c}|=\sqrt{37},\]then the angle between \[\vec{a}\]and \[\vec{b}\] is
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{\pi }{6}\]
done
clear
D)
\[\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 122) The position vector of a point lying on the line joining the points whose position vectors are \[\hat{i}+\hat{j}-\hat{k}\]and \[\hat{i}-\hat{j}+\hat{k}\]is
A)
\[\hat{j}\]
done
clear
B)
\[\hat{i}\]
done
clear
C)
\[\hat{k}\]
done
clear
D)
\[\vec{o}\]
done
clear
View Answer play_arrow
question_answer 123) If the volume of parallelepiped with\[4\hat{i}+5\hat{j}+\hat{k},-\hat{j}+\hat{k}\]with coterminous edges \[4\hat{i}+5\hat{j}+\hat{k},-\hat{j}+\hat{k}\] and \[3\hat{i}+9\hat{j}+p\hat{k}\]is 34 cubic unit, then? is equal to
A)
4
done
clear
B)
-13
done
clear
C)
13
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 124) If A and B are two independent events such that \[P(B)=\frac{2}{7},P(A\cup {{B}^{c}})=0.8,\]then \[P(A)\] is equal to
A)
0.1
done
clear
B)
0.2
done
clear
C)
0.3
done
clear
D)
0.4
done
clear
View Answer play_arrow
question_answer 125) Seven balls are drawn simultaneoulsy from a bag containing 5 white and 6 green balls. The probability of drawing 3 white and 4 green balls is
A)
\[\frac{7}{{{\,}^{11}}{{C}_{7}}}\]
done
clear
B)
\[\frac{{{\,}^{5}}{{C}_{3}}+{{\,}^{6}}{{C}_{4}}}{{{\,}^{11}}{{C}_{7}}}\]
done
clear
C)
\[\frac{{{\,}^{5}}{{C}_{2}}+{{\,}^{6}}{{C}_{2}}}{{{\,}^{11}}{{C}_{7}}}\]
done
clear
D)
\[\frac{{{\,}^{6}}{{C}_{3}}+{{\,}^{5}}{{C}_{4}}}{{{\,}^{11}}{{C}_{7}}}\]
done
clear
View Answer play_arrow
question_answer 126) The equation of the line passing through the point of intersection of the lines\[~x-3y+2=0\] and and perpendicular to the line \[2x+5y-7=0\] is
A)
\[2x-3y+1=0\]
done
clear
B)
\[~6x-9y+11=0\]
done
clear
C)
\[~2x-3y+5=0\]
done
clear
D)
\[3x-2y+1=0\]
done
clear
View Answer play_arrow
question_answer 127) Let O be the origin and A be a point on the curve \[{{y}^{2}}=4x.\]Then the locus of the mid point of OA, is
A)
\[{{x}^{2}}=4y\]
done
clear
B)
\[{{x}^{2}}=2y\]
done
clear
C)
\[{{x}^{2}}=16y\]
done
clear
D)
\[{{y}^{2}}=2x\]
done
clear
View Answer play_arrow
question_answer 128) The lines represented by the equation \[{{x}^{2}}-\text{ }{{y}^{2}}-\text{ }x+3y-2=0\]are
A)
\[x+y-1=0,\,x-y+2=0\]
done
clear
B)
\[x-y-2=0,x+y+1=0\]
done
clear
C)
\[x+y+2=,0,x-y-1=0\]
done
clear
D)
\[x-y+1=0,x+y-2=0\]
done
clear
View Answer play_arrow
question_answer 129) If OA is equally inclined to OX, OY and OZ and if A is \[\sqrt{3}\]unit from the origin, then A is
A)
\[(3,3,3)\]
done
clear
B)
\[(-1,1,-1)\]
done
clear
C)
\[(-1,1,1)\]
done
clear
D)
\[(1,1,1)\]
done
clear
View Answer play_arrow
question_answer 130) If the direction cosines of two lines are such that \[l+m+n=0,{{l}^{2}}+{{m}^{2}}-{{n}^{2}}=,0\]then the angle between them is
A)
\[\pi \]
done
clear
B)
\[\pi /3\]
done
clear
C)
\[\pi /4\]
done
clear
D)
\[\pi /6\]
done
clear
View Answer play_arrow
question_answer 131) The number of common tangents to the two circles \[{{x}^{2}}+\text{ }{{y}^{2}}-\text{ }8x+2y=0\] and \[{{x}^{2}}+{{y}^{2}}-2x-16y+25=0\]is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 132) The length of the tangent drawn to the circle \[{{x}^{2}}+{{y}^{2}}-2x+4y-11=0\]from the point \[(1,3)\]is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 133) Equation of the latusrectum of the ellipse \[9{{x}^{2}}+4{{y}^{2}}-18x-8y-23=0\text{ }\]are
A)
\[y=\pm \text{ }\sqrt{5}\]
done
clear
B)
\[x=\pm \text{ }\sqrt{5}\]
done
clear
C)
\[y=1\pm 5\]
done
clear
D)
\[x=-1\pm \sqrt{5}\]
done
clear
View Answer play_arrow
question_answer 134) If the eccentricity of a hyperbola is\[\sqrt{3},\], then the eccentricity of its conjugate hyperbola is
A)
\[\sqrt{2}\]
done
clear
B)
\[\sqrt{3}\]
done
clear
C)
\[\sqrt{\frac{3}{2}}\]
done
clear
D)
\[2\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 135) If \[{{x}^{y}}={{y}^{x}},\]then \[x(x-y\log x)\frac{dy}{dx}\]is equal to
A)
\[y(y-x\log \,y)\]
done
clear
B)
\[y(y+x\,\log \,y)\]
done
clear
C)
\[x(x+y\log x)\]
done
clear
D)
\[x(y-x\log y)\]
done
clear
View Answer play_arrow
question_answer 136) \[f(x)={{e}^{x}}\sin x,\]then \[f(x)\]is equal to
A)
\[{{e}^{6x}}\sin 6x\]
done
clear
B)
\[2{{e}^{x}}\cos x\]
done
clear
C)
\[8{{e}^{x}}\sin x\]
done
clear
D)
\[8{{e}^{x}}\cos x\]
done
clear
View Answer play_arrow
question_answer 137) If \[0<p<q,\]then \[\underset{n\to \infty }{\mathop{\lim }}\,{{({{q}^{n}}+{{p}^{n}})}^{1/n}}\]is equal to
A)
\[e\]
done
clear
B)
\[p\]
done
clear
C)
\[q\]
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 138) \[\underset{x\to \infty }{\mathop{\lim }}\,[{{x}^{2}}+2x-1]\]is equal to
A)
\[\infty \]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
4
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 139) If \[f(x)=\left\{ \begin{matrix} \frac{1-\sqrt{2}\sin x}{\pi -4x}, & if\,x\ne \frac{\pi }{4} \\ a & if\,x=\frac{\pi }{4} \\ \end{matrix} \right.\] is continuous at \[\frac{\pi }{4},\] then a is equal to
A)
4
done
clear
B)
2
done
clear
C)
1
done
clear
D)
1/4
done
clear
View Answer play_arrow
question_answer 140) If \[\theta \]is the angle between the curves \[xy=2\]and \[{{x}^{2}}+4y=0,\]then \[\tan \theta \]is equal to
A)
1
done
clear
B)
-1
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 141) In the interval \[(-3,3)\] the function \[f(x)=\frac{x}{3}+\frac{3}{x},x\ne 0\]is
A)
increasing
done
clear
B)
decreasing
done
clear
C)
neither increasing nor decreasing
done
clear
D)
partly increasing and partly decreasing
done
clear
View Answer play_arrow
question_answer 142) If \[\int_{{}}^{{}}{\,\sqrt{\frac{x}{{{a}^{3}}-{{x}^{3}}}}dx}=g(x)+c,\]then \[g(x)\]is equal to
A)
\[\frac{2}{3}{{\cos }^{-1}}x\]
done
clear
B)
\[\frac{2}{3}{{\sin }^{-1}}\left( \frac{{{x}^{3}}}{{{a}^{3}}} \right)\]
done
clear
C)
\[\frac{2}{3}{{\sin }^{-1}}\left( \sqrt{\frac{{{x}^{3}}}{{{a}^{3}}}} \right)\]
done
clear
D)
\[\frac{2}{3}{{\cos }^{-1}}\left( \frac{x}{a} \right)\]
done
clear
View Answer play_arrow
question_answer 143) If \[\frac{dx}{{{x}^{2}}+2x+2}=f(x)+c,\]then \[f(x)\]is equal to
A)
\[{{\tan }^{-1}}(x+1)\]
done
clear
B)
\[2{{\tan }^{-1}}(x+1)\]
done
clear
C)
\[-{{\tan }^{-1}}(x+1)\]
done
clear
D)
\[3{{\tan }^{-1}}(x+1)\]
done
clear
View Answer play_arrow
question_answer 144) \[\int_{0}^{\pi /2}{\frac{dx}{1+{{\tan }^{3}}x}}\]is equal to
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{3\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 145) The solution of\[(1+{{x}^{2}})\frac{dy}{dx}+2xy-4{{x}^{2}}=0\]is
A)
\[3x(1+{{y}^{2}})=4{{y}^{3}}+c\]
done
clear
B)
\[3y(1+{{x}^{2}})=4{{x}^{3}}+c\]
done
clear
C)
\[3x(1-{{y}^{2}})=4{{y}^{3}}+c\]
done
clear
D)
\[3y(1+{{y}^{2}})=4{{x}^{3}}+c\]
done
clear
View Answer play_arrow
question_answer 146) The function \[f(x)=\log (x+\sqrt{{{x}^{2}}+1})\]is
A)
an even function
done
clear
B)
an odd function
done
clear
C)
a periodic function
done
clear
D)
neither an even nor an odd function
done
clear
View Answer play_arrow
question_answer 147) If p, q and rare simple propositions with truth values T, F, T, then the truth value of\[(\tilde{\ }p\vee q)\wedge \tilde{\ }q\Rightarrow p\]is
A)
true
done
clear
B)
false
done
clear
C)
true, if r is false
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 148) The dual of \[x+(yx)=x\]is
A)
\[(x+y).(x+x)=x\]
done
clear
B)
\[x.(y+x)=x\]
done
clear
C)
\[x.(y.x)=x\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 149) Forces of magnitudes 5N, 10N, 15N and 20 N act on a particle in the direction of North, South, East and West respectively. The magnitude of their resultant is
A)
\[15\sqrt{2}N\]
done
clear
B)
\[10\,N\]
done
clear
C)
\[25\sqrt{2}\,N\]
done
clear
D)
\[5\sqrt{2}\,N\]
done
clear
View Answer play_arrow
question_answer 150) The value of \[\int_{-\pi /2}^{\pi /2}{\log \left( \frac{2-\sin \theta }{2+\sin \theta } \right)}d\theta \]is
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
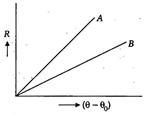 conditions. What inference do you draw from their cooling curves?
conditions. What inference do you draw from their cooling curves?